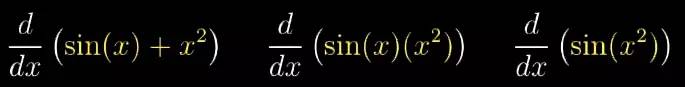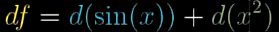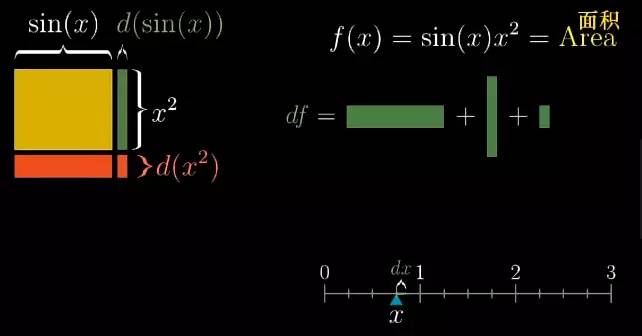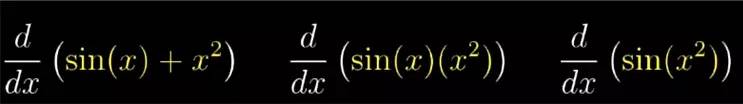【直观理解链式法则和乘积法则】- 微积分的本质 04

 在前几期的视频中, 我们讨论了简单函数的导数, 目的是解释这些公式的来源, 你让脑中有得清晰直观的图像. 不过现实中我们用的大多数函数都需要或多或少地将这些简单函数进行组合. 为我们现在的目标是理解这些更复杂的组合, 如何进行求导.

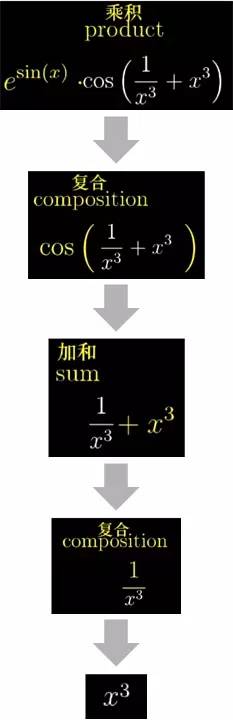
让你对每条法则的来源都有一幅清晰的图像, 这就归结为三种组合函数的基本方法: 函数相加, 函数相乘以及复合函数. 你遇到的大部分函数就只包括这三种组合方式的层叠

只要你掌握了这三种组合方式的导数, 你就总能将一个庞大的表达式一层一层的剥离，一步一步的求导.

所以问题就是, 如果你知道两个函数的导数, 它们的和, 乘积以及合成后的函数的导数是什么?

加法法则

加法法则是最简单的, 两个函数的和的导数就是它们的导数的和.

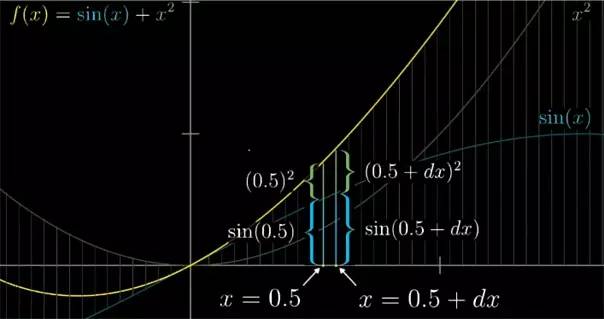
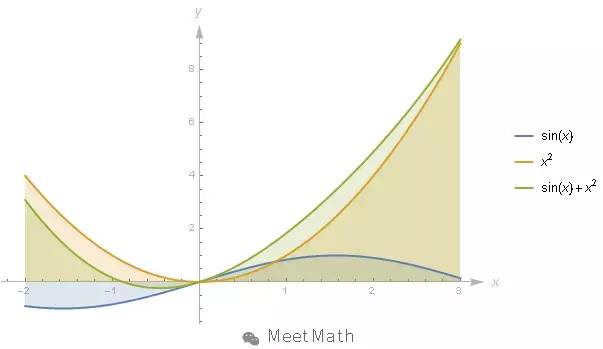
让我们仔细的考虑上面的加法法则, 例如，要么考虑函数 $f\left(x\right)=sin\left(x\right)+x^2$ , 在每一个变量取值上, 就把$sin\left(x\right)$和$x^2$相应的函数值相加.

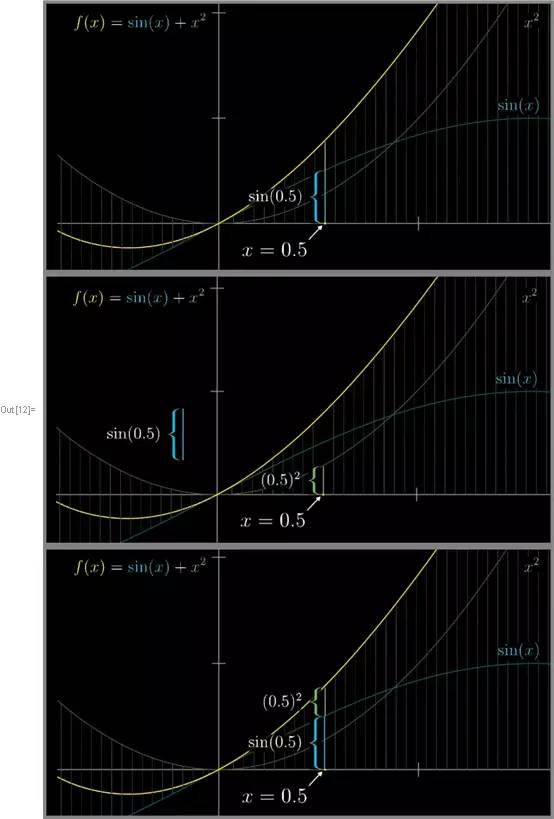
比如在$x=0.5$处, 正弦函数图像的高度就是这一段, 三个函数在此点的图像为下面所示:

等于导数, 你就看看 x 稍作变化之后会发生什么? 比如增加 $dx$

这两点的函数值的差就叫做 d$f$. 画出图像之后, 就会很清楚地看到图像高度的总变化量, 就是正弦图像函数的变化量 dsin(x)加上 $x^2$的变化量, 也就是 d$\left(x^2\right)$.

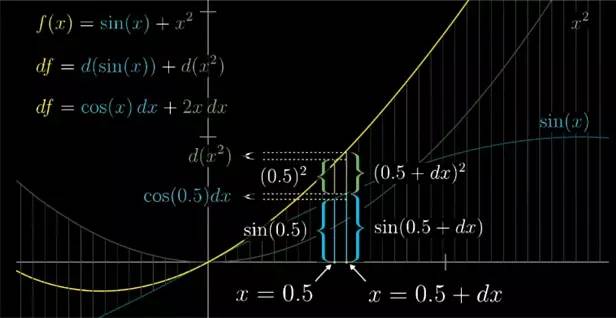
我们知道正弦的导数是余弦, 这意味着, 这个变化量 dsin(x) 差不多是cos(x) dx ,  它和 x 的变化量 dx 的大小成正比.

类似地, 因为 $x^2$ 的导数是 2x, 所以 $x^2$ 图像的高度变化大约是 $2\ast x\ast dx$. 所以 $\frac{df}{dx}$ , 也就是和函数微小变化与自变量 x 微小变化的比值, 确实就是 $cos\left(x\right)+2x$, 也就是各部分导数的和.

乘积法则

类似地, 我们通过微小变化思考乘积的法则. 通过面积来理解乘积法则, 矩形的边长是 $sin\left(x\right)$ 和 $x^2$ . 因为它们都是函数, 所以可以认为这些边长能够变化, 而且都取决于 x , 你可以认为这个数能够自由变大变小.

观察图形, 它按照函数 sin(x) 变化, 当 x 从 0 开始增长, 当 sin(x) 接近它的峰值时, 这条边的长度会增加到 1. 然后长度开始减小，因为sin(x) 从 1 开始下降. 同样的高度会按照 $x^2$ 变化.

所以由乘积定义的 f(x) 就是这个盒子的面积, 对于导数, 思考一下 x 的微小变化, $dx$ 将如何影响面积. 由它导致的面积变化 $df$是多少呢？

x 的微小变化 $dx$ 使得宽度变化了 d(sin(x)) , 而高度变化了 d($x^2$). 这就产生了三个小块儿新的面积.

而第三部分我们可以忽略它, 因为它的面积最终会正比于 $d{x}^2$. 我们知道, 当 $dx$ 逼近 0 的时候, 它就可以被忽略掉.

这推理过程对任意两个函数 g 和 h 都适用,能帮助你记忆乘法法则的一个口诀就是:

对于上例来说就是:

如函数和一个常数相乘, 比如 2 乘以 sin(x)，事情最终会简单许多. 它的导数就是同样的常数乘以函数的导数. 根据下面图形考虑来验证结果.

复合函数

还有一种常见的函数组合方式, 它出现的极为频繁, 那就是把一个函数塞到另外一个里面, 也叫做函数复合.

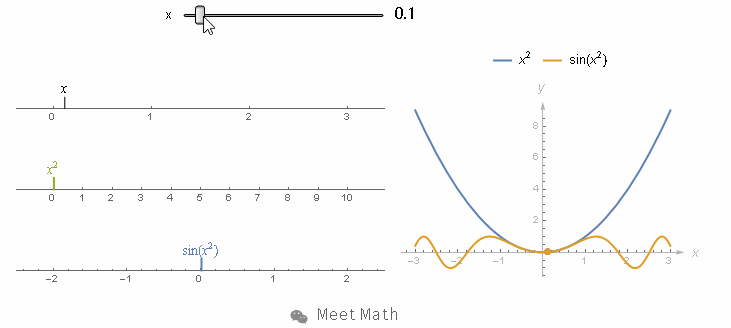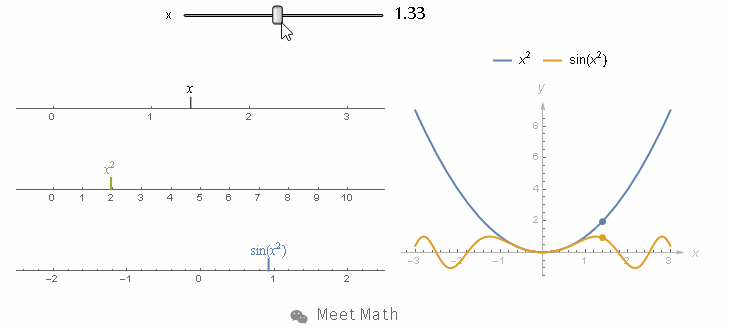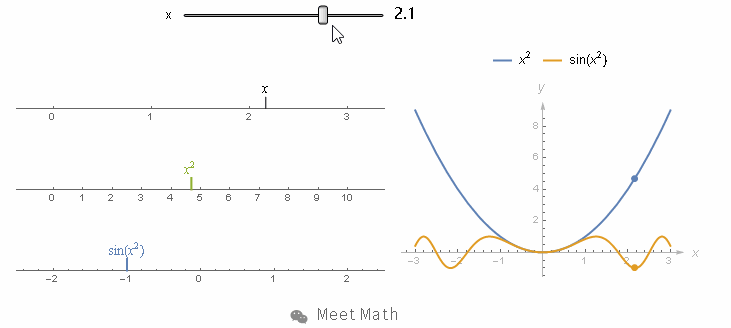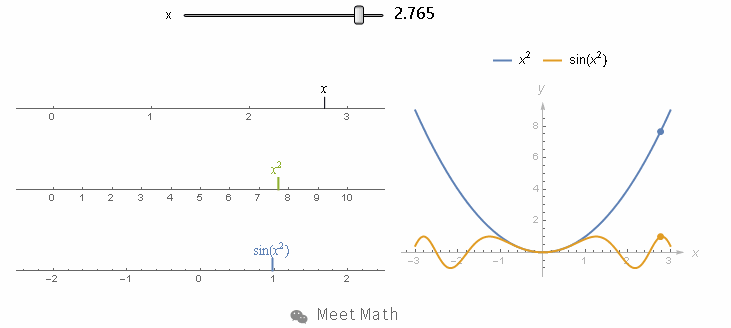
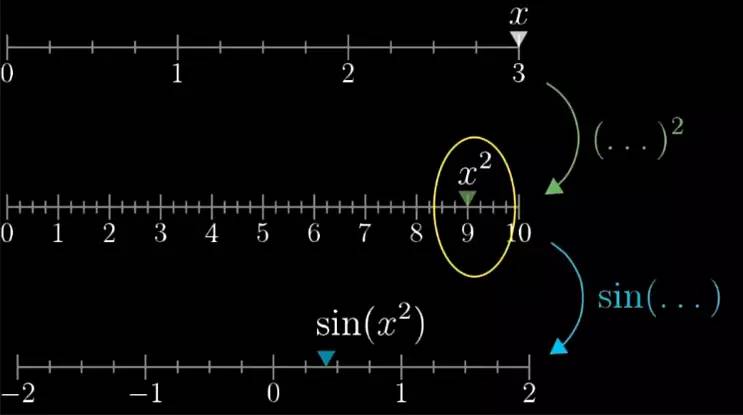
再换一种方法来可视化, 列出三条数轴, 最上面的数轴代表 x 的值, 第二条数轴代表 $x^2$ 的值, 而第三条数轴代表 sin($x^2$) 的值.

也就是说函数 $x^2$ 把自变量从数轴 1 带到数轴 2, 而正弦函数把上个结果从数轴 2 带到数轴 3.

但我改变 x 的值, 比如让它增加到 3 时. 第二个数轴上的刻度，就会跑到 9 , 而最下面的数轴上就会跑到 sin(9) 位置.

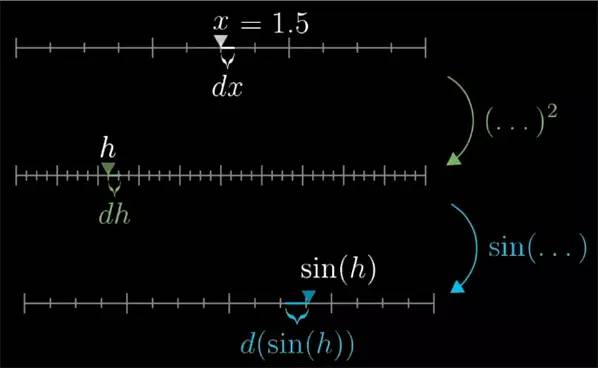
想要计算导数，我们还是一样 x 稍微变化 $dx$ 的量, 并且我们把 x 做一个具体的值， 比如说1.5 会帮助理解. 它所导致的第二个值的变化量, 即 $dx$ 引起的 $x^2$ 的变化, 就是 d($x^2$), 展开为 $2\ast x\ast \text{dx}$. 对于这个特定的 x 值, 这就是 $2\ast 1.5\ast \text{dx}$.

其实更进一步, 给 $x^2$ 一个新的名字, 叫做 h, 那么 d($x^2$) 这个变化量就是 dh . 这就方便了我们考虑了第三个值 sin(h). 由于 h 有 dh 的变化, 所以 sin(h) 也增减了 d(sin(h) 的量.

顺便说一句, d(sin(h)) 向左移动而 dh 向右移动, 说明 d(sin(h)) 这个变化量是一个负值.

我们可以把 d(sin(h)) 展开为 cos(h)*dh, 这就是正弦的导数是余弦的意思. 再做展开, 用 $x^2$ 替换 h . 最下面的变化量就是 cos($x^2$)*d($x^2$).

注意到 d($x^2$) 就是 2x*$dx$ 我们还可以进一步展开.

常常回想起一个表达式的意义, 总是一个好习惯. 这个例子里, 我们从最上面的 $x=1.5$ 开始, 这告诉我们第三条数轴上的变化量.

这就是我们所说的链式法则(Chain Rule)

嗯，注意, 对于 g 导数我的是 $\frac{dg}{dh}$, 而不是 $\frac{dg}{dx}$. 从符号层面看，这是在提醒你. 你往这个导数里带入的仍旧是内层函数, 但它也很重要地反映了外层函数的导数究竟代表着什么？

记得在用三条数轴表示的时候, 当我们对最下面的正弦函数求导, 我们把变化量 d(sin(h)) 展开为 cos(h)*dh. 这是因为我们不能立即知道最下面的变化量与 x 的依赖关系. 它是我们试图求助的总量, 但是我们可以对中间变量 h 求导, 也就是说把第三行的变化量, 表示第二行的变化量的 dh 倍数. 然后再进一步求出 dh 是什么？

所以链式法则的表达式是在说, 看看输出值 g 的微小变化除以 h 的微小变化是多少(h 就是要代入函数 g 的值), 然后乘以 h 的微小变化与 x 的微小变化的比值. 这些 dh 最终将被消去, 结果就是输出值 g 的微小变化，与输入 x 的微小变化的比值.

dh 的消去并不只是符号上的技巧, 而是真实地反映出了我们在求导数的时候, 各种微小变化量发生了什么.

现在我们手头上有三种工具来处理简单函数组合出的函数的导数: 加法法则, 乘法法则以及链式法则.

只是观看视频，是不可能代替自己去做练习, 要去锻炼自己计算的能力. 所以练习这件事恐怕要你自己来做. 我希望你展示的是这些法则的来源, 说明它们并不是死记硬背的东西, 而是很自然的规律.

未来会持续升级, 继续对此套视频的整理为文字版, 届时公众号会发布;

因为水平有限, 疏忽错误在所难免, 还请各位老师和朋友多提宝贵意见, 帮助我们改进这个系列, 感谢感谢!

视频可以在[遇见数学]公众号后台, 分别输入关键字[高等数学]直接得到下载地址. 

查看之前发布《图解高数系列》

编辑 | 李想

制作 | 公理