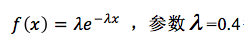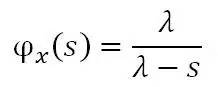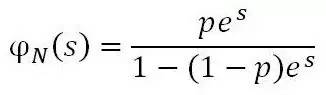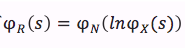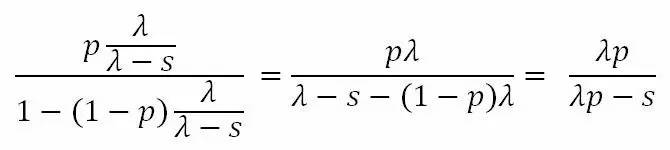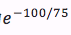学好概率，遇见百分百女孩……（高能提示：能遇见，但没用）

编辑：小庄

 

众所周知，果壳聚集了一大群有趣的灵魂

不知道你还记不记得这一只，哦不，这一位，他叫叶丙成——

看起来，有点像梁朝伟艺术家对吧？

但实际上，他是一位，数学老师

（噢漏！！）

没错，他就是一位数学老师，而且有一长串title，如下，本AI来给你快板状态念一下—— 

第一个

在由斯坦福大学两位计算机教授开办的网络公开课平台Coursera上以华语讲课的老师

世界上第一个

将大规模开放式线上课程（MOOC）变成多人线上竞技游戏的老师

全球共计超过六万名学生修课，是两岸三地教过最多学生的工程教授

当代第一个

推行“意识流概率文学创作”的老师

有史以来第一个

扎着马尾辫见校长的台湾大学电机系老师

带领学生团队击败 43 国 426 名校团队赢得Wharton-QS “Reimagine Education”首届世界教学创新大奖的老师

…… 

好了以下说正事儿，这位叶老师最近带着他的弟子们在果壳阅读出了一本书，书名一听就会让你们倍儿精神，《MOOC概率考题书》——

（摄影：Big D）

有没有头皮隐隐发麻，回忆起大学时坐在考卷前的抓耳挠腮？

事实上编辑小庄就能回忆起她大二概率考试前蜷在宿舍走廊上背了120多个公式的那个夜晚，要命的是与此同时隔壁寝室一直在电台里播放流行女作家的言情小说，鬼知道她是怎么考了92分的（应该没记错吧）……

事实上，多年以后，小庄觉得，概率和爱情之间真的有着千丝万缕的联系，这一切已经在考试前的那个晚上注定。因为在2017年她有幸以策划者和出版人的身份，向大家推出了这本口号叫做“用27个通俗易懂的故事教你学好概率/了解世界的运行规律/找到百分百女孩”的书，这里面的故事，不瞒你说，不少和爱情有关，有来自村上春树小说的，有来自《仙剑》的（不是逗你），也有来自普通大学理工科男生的白日梦。总之，不像你想的那样，它一点也不艰涩，里面充满了文学气息，和有趣的构想，有一些让你大笑，有一些让你淡淡哀伤。

然而在背后，它是由条件概率、随机变量、概率质量函数、累积分布函数、概率密度函数、期望值组成的。

就是有那么神奇，它在一种精确锚定的计算中诉说着人生的各种悲欢离合可能性。

本篇推送特地选了其中最美好忧伤的一篇《某个晴朗的早晨遇见100%的女孩》以飨读者，当然，目的就是让你，买书，它不会让你失望的，相信我

 

某个晴朗的早晨

遇见100%的女孩

 

难度：★★★

使用技巧：解题时需要了解动差函数的意义，并且了解几何分布与指数分布所给定参数的意义，之后直接求取所需概率。

原作者：林宗毅、黄彦澄、施保全

那故事从“从前的从前”开始，以“你不觉得很悲哀吗？”结束。

从前的从前，有一个地方，有一位少年和一位少女。少年十八岁，少女十六岁。少年并不怎么英俊，少女也不怎么漂亮。是任何地方都会有的孤独而平凡的少年和少女。不过他们坚决地相信，在这世界上的某个地方，一定有一位 100%跟自己相配的少女和少年。

有一天，两个人在街角偶然遇见了。

“好奇怪啊！我一直都在找你，也许你不会相信，不过你对我来说，正是100%的女孩子呢。”少年对少女说。

少女对少年说：“你对我来说才正是 100%的男孩子呢。一切的一切都跟我想象的一模一样。简直像在做梦嘛。”

两个人在公园的长椅上坐下，好像有永远说不完的话，一直说下去，彼此觉得再也不孤独了。追求 100%的对象，被 100%的对象追求，是一件多么美妙的事啊！可随着谈话继续，男孩和女孩的心里，却不由得闪现出一点点的疑虑，就那么一点点梦想，就这么简单地实现，是不是一件好事呢？谈话忽然中断的时候，少年这么说道：

“让我们再试一次看看。如果我们两个真的是 100%的情侣的话，将来一定还会在某个地方再相遇，而且下次见面的时候，如果互相还觉得对方是 100%的话，那么我们马上就结婚，你看怎么样？”

“好哇。”少女说。

于是两个人就分手了。

其实说真的，实在没有任何需要考验的地方；因为他们是名副其实 100%的情侣。而且命运的波涛是注定要捉弄有情人的。然而，来年冬天，男孩得了流行的恶性流行性感冒，好几个星期都一直在生死边缘挣扎的结果，往日的记忆已经完全丧失，当他在来年次年的秋天醒过来的时候，他的脑子里已经像少年时代的 D. H. 劳伦斯的钱包一样空空如也。

女孩每年四月某日晴朗的早晨在那个街角穿梭。

 

之后，男孩努力再努力后，总算又获得了新的知识和感情。并且顺利地重回社会。他也能好好地搭地下铁换车，也能到邮局去发限时专送，也经历着 75%的恋爱，或 85%的恋爱。

女孩依然每年四月某日晴朗的早晨在那个街角徘徊。

随着时间流逝，深藏在男孩脑海深处，关于女孩的记忆，逐渐复苏，他以每年平均2.5%的分量，依照指数分布的方式exponential(0.4)的增长。也就是

每隔一年，他就稍微记起那位女孩，从0%，到2.5%，一路慢慢成长。

而就算没有完全想起，但他的身体很自然而然地，彷佛反射动作一样，每年也会在四月某个晴朗的早晨，为了一杯 Morning Service 的咖啡，在一条巷子里由东向西走去，然后经过那个街角。

那是女孩每年四月的某个早晨，都会站在那儿等待的街角。

由于彼此原是100%的男孩女孩，所以不管等多少年，两人必然会再次相遇的。但每年也就只有1/30的机率，男孩会遇上在那等待的女孩。

也因此，再次相遇的年数N，便呈几何分布(geometric distribution)

(在第N年遇见的机率分布)

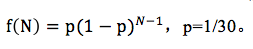
然而，尽管女孩仍记得他是100%的男孩，男孩却不一定恢复到能立刻认出她是100%的女孩了。

男孩遇见女孩当下的总百分数，是以指数分布(一年的百分数)，累积几何分布次的(第几年遇见)一个新的分布。以卷积计算过于复杂，因此我们需要动差生成函数[1](moment generatingfunction: MGF)的帮助。

（[1]即矩量生成函数，在统计学中，矩也被叫做动差。）

指数分布的动差生成函数为

几何分布的动差生成函数为

N年累积的总X，称为R，便有

带进去后即是

可以看见R的动差生成函数跟指数分布的X一致，所以R也是指数分布，参数为λp，也就是1/75。指数分布的累积分布函数(CDF)为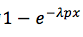，x用100代入可以得到男孩遇见女孩总%数小于等于一百的机率，那大于或等于100%的机率亦即为

——大约是26.4%，他们看见彼此时，眼中的对方是100%或以上的男孩女孩。

她对我来说，真是 100%的女孩呀！

他对我而言，正是 100%的男孩啊！

尽管男孩可能再次发现了对方是100%的女孩，但他的记忆之光实在太微弱了，声音也不再像以往那么清澈了，在女孩发出声前，他一语不发地擦肩而过，就这样消失到人群里去了。

然后两人就再也没有相遇了。

那么，你不觉得很悲哀吗？

 

——改编自村上春树，《遇见 100%的女孩》

 

关于这本书的初衷，叶丙成老师是这么说的——

还记得三年前某日，我在台大电机必修课“机率与统计”班上跟大家说：“以后有一天，我们一定会出版一本书，让这个世界看到你们超级精采的创作才华！”三年后的今天，我们终于做到了！

参与本书编辑和创作的还包括以下若干位同学

台湾师范大学电机工程学系助理教授

2016 年“菠萝科学奖”数学奖得主

数学作家

赖以威

 

前排从左到右依次是

萧乐山、陈威宇、谢瑞贤、黄大珉

后排从左到右依次是

陈鸿猷、朱柏宪、柯劭珩、郑子宇

 

最后po上小庄的新书广告新发型皂片，看看这配色你就知道她为了推荐此书是多么全力以赴，所以，请点击阅读原文，下单吧！

本文来自果壳网，谢绝转载

如有需要请联系sns@guokr.com

（欢迎转发到朋友圈~）

果壳网

ID：Guokr42

果壳整天都在科普些啥啊！

吓得我二维码都屈光不正了！

放心，你没瞎。

为啥这样的二维码也能扫？

扫码发送【二维码】告诉你原理~