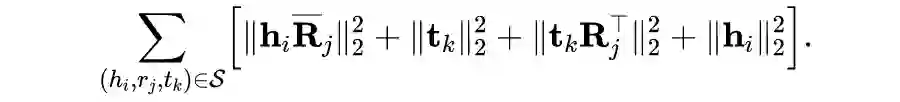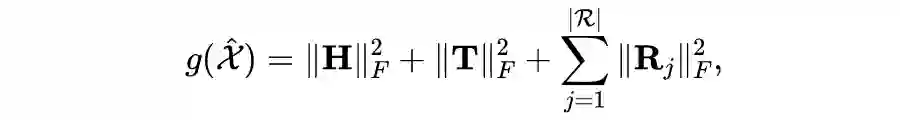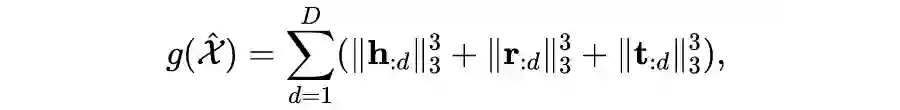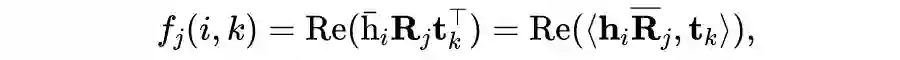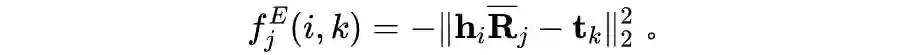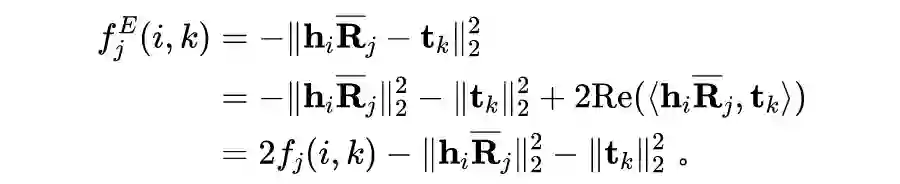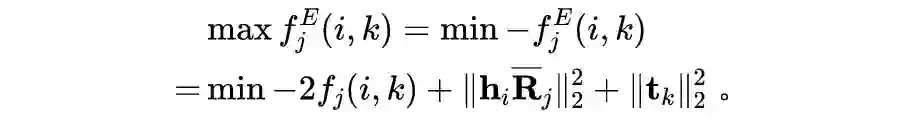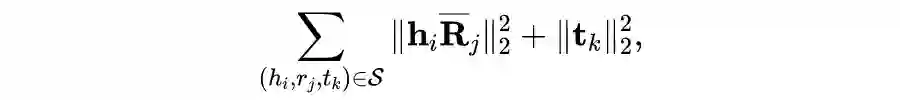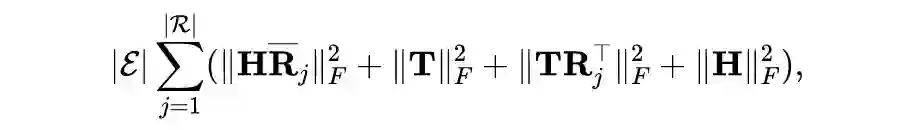NeurIPS 2020 | 面向张量分解知识图谱补全的对偶诱导正则

2020 年 12 月 19 日 PaperWeekly

简介

近年来，张量分解模型凭借模型简洁、计算速度快等优点在知识图谱补全任务上取得了令人瞩目的成就。但是，这些模型较易受到过拟合的影响，在性能上通常落后于其他类型的模型。为解决过拟合问题，包括 L2 正则，N3 正则 [1] 在内的多种正则项被提出，但这些正则项又在性能或者适用范围上存在明显缺陷。

为此，我们基于知识图谱补全模型之间的对偶性，为张量分解模型提出了一种新的正则项——DURA。该正则项可以广泛地应用于多种不同的张量分解知识图谱补全模型，且能够显著提升模型性能。

论文标题：

Duality-Induced Regularizer for Tensor Factorization Based Knowledge Graph Completion

论文链接：

https://papers.nips.cc/paper/2020/hash/f6185f0ef02dcaec414a3171cd01c697-Abstract.html

代码链接：

https://github.com/MIRALab-USTC/KGE-DURA

知识图谱补全

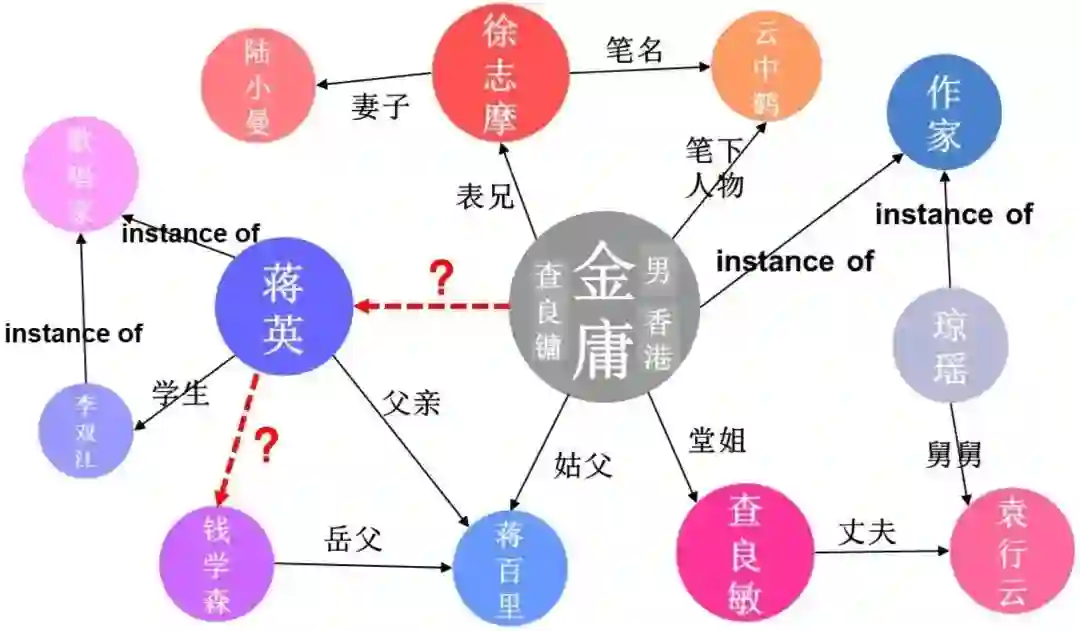
知识图谱由大量的事实三元组构成，其存储了结构化的人类知识。例如，下图中的（金庸，笔下人物，云中鹤）和（金庸，姑父，蒋百里）都是事实三元组。

尽管常用的知识图谱具有十亿乃至以上级别的三元组，但其中仍会存在大量的三元组缺失。例如，下图中”蒋英“和”钱学森“之间缺失了”丈夫“关系，”金庸“和”蒋英“之间缺失了”表姐“关系。因知识图谱的规模通常极为庞大，人工对图谱进行补全代价高昂。因此，基于知识图谱中的已知三元组来自动预测缺失三元组的知识图谱补全（Knowledge Graph Completion, KGC）技术近年来备受关注。

形式化描述

给定一个由实体构成的集合和一个由关系构成的集合，一个知识图谱

是一个三元组的集合，其中是第个实体，是第个关系。通常和也分别称为头实体和尾实体，有时也会被写成 (head) 和 (tail)。知识图谱补全的目标是根据中已知的三元组来预测未知的正确三元组。

我们通常将知识图谱补全问题建模成一个给定头（尾）实体和关系的尾（头）实体预测问题。如在问题中给定来预测尾实体。

知识图谱补全模型通常先将每个实体与关系映射为低维嵌入和（knowledge graph embeddings，可为向量/矩阵/张量），然后通过一个以低维嵌入为输入的打分模型为给定三元组进行打分，从而确定任意三元组真实存在的概率（即置信度）。如果一个补全模型足够好，那在这一问题中，能够使得三元组成立的尾实体得分应该高于其他实体。

知识图谱补全模型

4.1 两类重要模型

「基于距离的模型」 (distance-based models) 和「基于张量分解的模型」 (tensor factorization-based models) 是两类重要的知识图谱补全模型。

基于距离的模型使用闵可夫斯基距离来度量三元组的合理性，其一般具有如下形式。

其中是与模型相关的函数。

虽然这类模型能够达到较好的性能，但在建模复杂的关系模式（如一对多和多对一关系）时仍然存在困难。
基于张量分解的模型将知识图谱视为部分可观测的三阶张量，当是正确三元组时，，否则。因此，知识图谱补全被建模为一个张量补全问题。

假设表示的第个前向切片，即第个关系的邻接矩阵。一般情况下，基于张量分解的知识图谱补全模型将近似分解为，其中的第行是，是第个关系对应的嵌入矩阵，和分别是复矩阵的实部和共轭（实矩阵的实部和共轭是它本身）。也就是说，打分函数被定义为。基于张量分解的模型的目的是寻找矩阵，使得可以近似。

从理论上讲，张量分解模型表现力强，能够很好地处理复杂的关系。然而，它们的往往面临「严重的过拟合」问题，无法达到最佳性能。因此，我们通常会在训练模型时加入「正则」入。

令，而是一个第个前向切片为的张量，则正则化后的基于张量分解的知识图谱补全模型可以写成

其中是固定参数，衡量与之间的差异，而是正则函数。

4.2 面向张量分解知识图谱补全的正则

针对张量分解模型，目前流行的正则项主要包括正则和正则。

正则是最常用的正则项，具有如下形式

其又被称为平方 Frobenius 正则。从上式这可以看出，正则能够应用于绝大部分张量分解模型，但实验表明，其并不一定能够带来稳定的性能提升 [2] 。

正则 [1] 即张量 3 阶核范数 (tensor nuclear-3 norm) [3] 正则，其适用于为对角矩阵的模型，具有如下形式

其中和分别是矩阵和的第列。假设是一个由的对角元组成第行的矩阵，则是矩阵的第列。实验表明，正则在为对角矩阵时（如 CP 和 ComplEx）能带来稳定的性能提升，但其不适用于为非对角阵的更一般情况（如 RESCAL）。

因此，我们还需要一个适用范围广且能带来稳定性能提升的正则项。

对偶诱导正则 DURA

5.1 Basic DURA

考虑一个知识图谱补全问题，即已知头实体和关系来预测尾实体。假设用来衡量给定三元组的置信度，则上一节中提到的基于张量分解的模型的打分函数可以写成

它首先通过一个线性变换对实体嵌入做一个映射，然后使用内积的实部来度量和之间的相似性。我们可以用另一个常用的相似性度量欧几里德距离可以代替上述等式中的内积相似性. 从而得到一个与之对应的基于距离的模型：

因平方打数函数和无平方的形式是等价的，我们事实上得到了以下「对偶性」：对于现有的基于张量分解的知识图谱补全模型（原模型），通常还有另一个与之相对应的基于距离的知识图谱补全模型（对偶模型）。具体地，原始模型和对偶模型之间的「对偶关系」又可以表示为

假设是所有已知正确三元组的集合。当我们训练一个基于距离的模型时，我们通常会在上最大化，而从上式我们知道

很显然，恰好是未加正则的张量分解模型的目标。因此，对偶关系为我们提供了如下正则项

我们称上述正则项为 Basic DURA。

很明显，Basic DURA 适用与为非对角阵的倾向，适用范围相较正则更广。

5.2 Basic DURA 为何有效

我们将从直觉上给出 Basic DURA 为何能够有效提升张量分解知识图谱补全模型的性能。如果多个尾实体能够使得三元组成立，那么DURA将促使它们具有相似的嵌入（embeddings）。

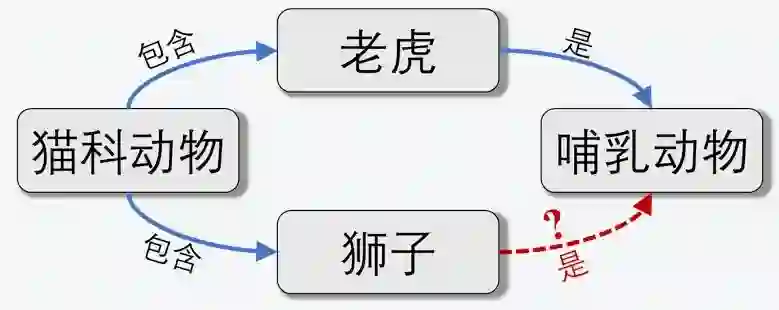
首先，我们可以断言，如果多个尾实体能够使得三元组成立，他们应该具有相近的语义。如在下图中，我们已知（猫科动物，包含，老虎）和（猫科动物，包含，狮子）两个三元组，则实体”老虎“和”狮子“在语义上是相近的。

进一步，我们可以断言，如果两个实体具有相近的语义，那么它们应该具有相似的嵌入。如果”老虎“和”狮子“具有相似的嵌入，我们又已知（老虎，是，哺乳动物）这一三元组，那么我们就可以对（狮子，是，哺乳动物）这一未知三元组进行补全。

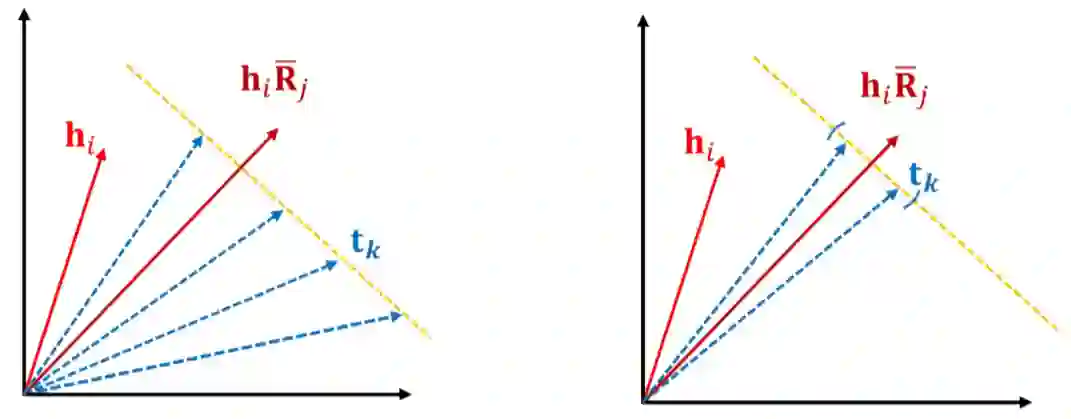
然而，由于内积相似度度量的特性，在一个基于张量分解的知识补全模型中，即使尾实体具有完全不同的嵌入，三元组也可以具有相同的打分（如下左图所示）。这在一定程度上会影响对未知三元组的预测。

在加入 DURA 之后，我们事实上通过欧氏距离引入了和应该较为相近的先验，因此尾实体的嵌入会被限制在一个较小的范围内（如下右图所示），从而有利于知识图谱的补全。

5.3 DURA

由内积的性质我们可知，利用与 Basic DURA 相似的推导过程，我们可以从对偶性中得到另一个正则项

类似地，当多个头实体能够使得三元组成立时，该正则项能够使得这些头实体的嵌入较为接近。

将两个不同方向的正则项相结合，我们得到「对偶诱导正则」（「DU」ality-induced「R」egul「A」rizer, 「DURA」）的最终形式

5.4 DURA的理论性质

当我们放宽正则项的求和条件至所有可能的实体和关系，DURA 具有如下形式

其中和分别是实体和关系的数目。

如果我们进一步假设关系嵌入矩阵为对角阵，我们有如下定理

在上述定理中，是张量的 2 阶核范数（nuclear 2-norm）[引用nuclear]，即矩阵迹范数（trace norm）在张量情形下的推广。

上述定理说明，在给定一些假设的情况下，DURA 事实上给出了张量的 2 阶核范数的一个上界。

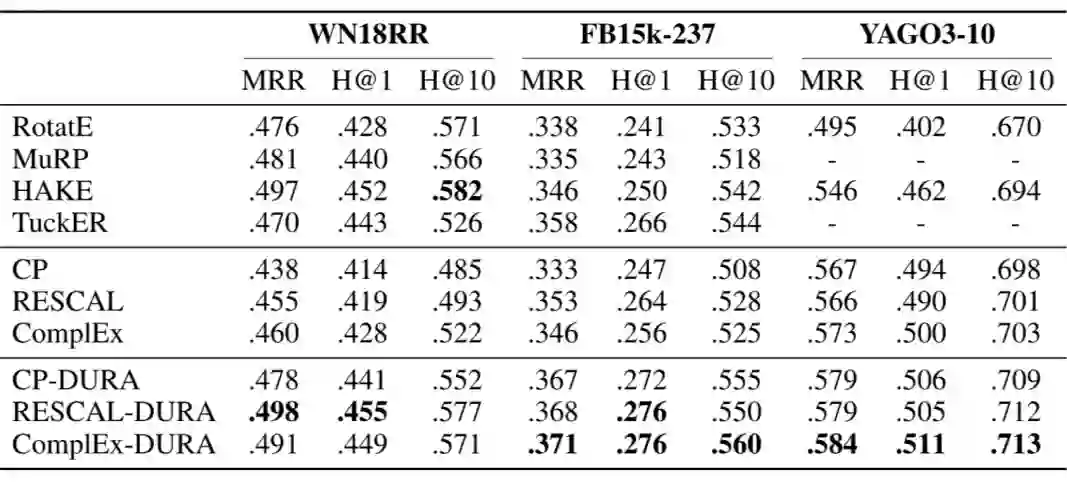
实验结果

6.1 知识图谱补全任务

我们在三个常用知识图谱补全数据集 WN18RR、FB15k-237、YAGO3-10 上验证了 DURA 的有效性。所考虑的基于张量分解的知识图谱补全模型包括目前流行的 CP、ComplEx [4] 和 RESCAL [5]。所采用的评价指标包括 MRR（Mean Recipocal Rank），H@N（Hits at N, N=1,10），越高的 MRR 和 H@N 代表越好的性能。实验结果如下表所示。

可以看出，DURA 为三个模型带来了稳定的性能提升。尤其值得一提的是，RESCAL 作为最早被提出的知识图谱补全模型之一（2011年），因其参数量较大而较易过拟合，在过去的几年中表现一直较差。但在加入 DURA 后，RESCAL 在 WN18RR 上取得了 MRR 为 0.498 的好成绩，超越了之前的所有模型。

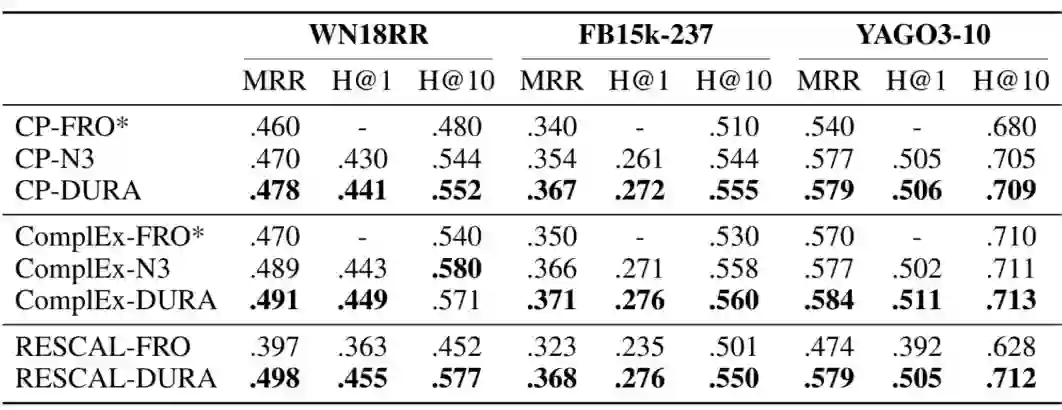
6.2 与其他正则的对比

我们在 CP、ComplEx 和 RESCAL 三个模型上对比了 DURA、（即 FRO)、三种正则的性能，结果如下表所示。注意无法应用于 RESCAL 模型。

从上表中可以看出，相比和正则，DURA 在适用范围和有效性上都具有明显优势。

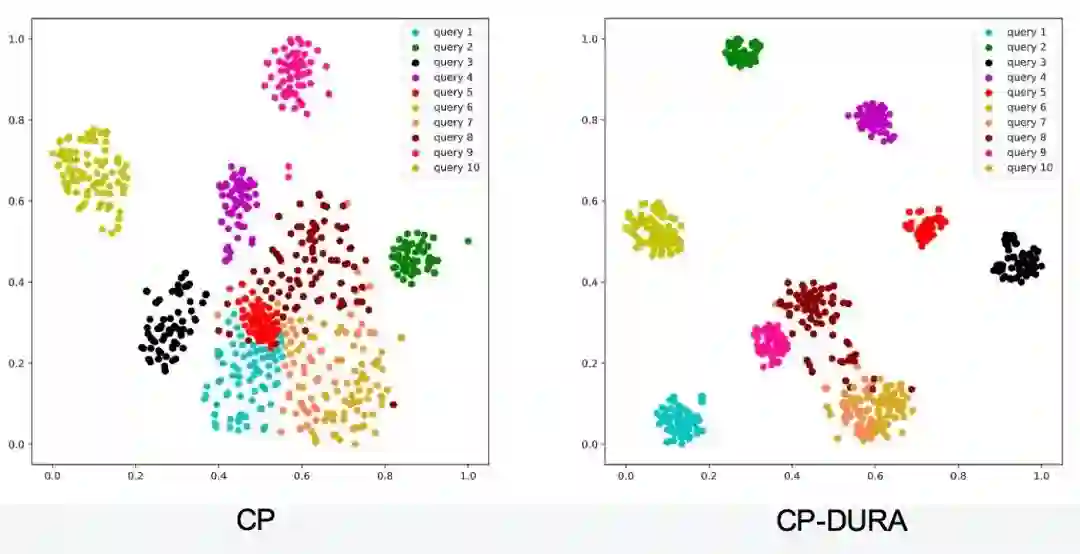
6.3 可视化

为验证”如果多个尾实体能够使得三元组成立，那么 DURA 将促使它们具有相似的嵌入（embeddings）”这一描述，我们利用 T-SNE 对加入 DURA 前后的实体嵌入进行了可视化。结果如下图所示，其中每一个数据点代表一个尾实体，而相同颜色的数据点代表这些尾实体能够使得同一成立。

从上图可以看出，在加入 DURA 后，能够使得同一成立的尾实体将倾向于拥有更为相似的嵌入。

总结

在知识图谱补全任务上，基于张量分解模型和基于距离的模型之间具有对偶性质，利用该对偶性，我们提出了一种面向张量分解模型的对偶诱导正则 DURA。DURA 能够广泛应用于多种不同的张量分解模型，且能够带来稳定而又显著的性能提升。

关于作者

张占秋，2018 年毕业于中国科学技术大学数学科学学院，获得理学学士学位。现于中国科学技术大学电子工程与信息科学系的 MIRA Lab 实验室攻读博士生，师从王杰教授。研究兴趣包括知识图谱与自然语言处理。

参考文献

[1] Lacroix, T., Usunier, N. & Obozinski, G.. (2018). Canonical Tensor Decomposition for Knowledge Base Completion. Proceedings of the 35th International Conference on Machine Learning, in PMLR 80:2863-2872

[2] Ruffinelli, D., Broscheit, S., & Gemulla, R. (2019). You CAN teach an old dog new tricks! on training knowledge graph embeddings. In International Conference on Learning Representations.

[3] Friedland, S., & Lim, L. H. (2018). Nuclear norm of higher-order tensors. Mathematics of Computation, 87 (311), 1255-1281.

[4] Trouillon, T., Welbl, J., Riedel, S., Gaussier, E. & Bouchard, G.. (2016). Complex Embeddings for Simple Link Prediction. Proceedings of The 33rd International Conference on Machine Learning, in PMLR 48:2071-2080.

[5] Nickel, M., Tresp, V., & Kriegel, H. P. (2011). A three-way model for collective learning on multi-relational data. Proceedings of the 28th International Conference on Machine Learning, in PMLR 11:809-816

更多阅读