AI学高数达到MIT本科水平，学了微积分线性代数概率论等6门课，不光能做题还能出题

梦晨 发自 凹非寺
量子位 报道 | 公众号 QbitAI

让语言模型做数学题，有多难？

强如GPT-3，在9-12岁的小学数学上，第一次才考20多分。

去年底GPT-3用上新方法努力了很久终于拿到55分，可惜还是没及格。

万万想不到啊，2022年才刚开始，突然有人宣布他们的模型掌握了高数，达到MIT本科水平。

AI学了6门MIT本科基础数学课里随机抽取的例题，都是网上就有的公开课，包括：

单变量微积分(课程编号18.01)
多变量微积分(18.02)
微分方程(18.03)
概率与统计入门(18.05)
线性代数(18.06)
计算机科学中的数学(6.042)

那么AI最后学到什么水平呢？

6门课程每门随机出25道题，再加上一个ACT水平（美国高考）的数据集里的60道题。

总计210道题，AI全部答对。

题目包括需要求出具体数值的，比如菌落繁殖的经典问题。

也有要求给出方程式的。

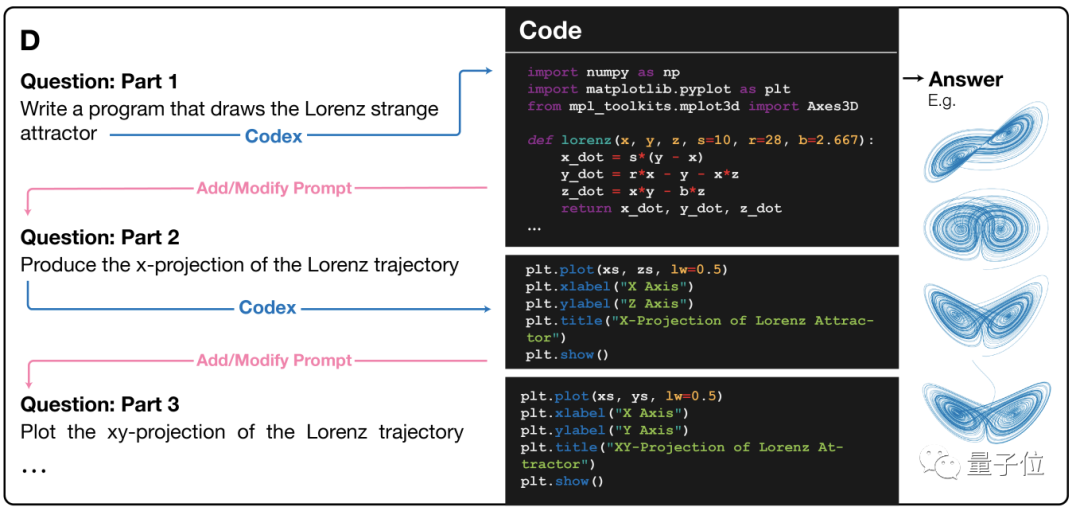
要求画出函数图像的也没问题。

最后为了证明训练出来的AI没有过拟合，还额外加试了一场应用线性代数(COMS3251)。

这门课不是公开课，网络上根本没有，也就是说AI在预训练阶段不可能接触到，结果AI也掌握了。

要知道在短短几个月前，AI还在挣扎于“小明种了5颗柠檬树，每年从每棵树上得到6个柠檬，10年间他总共得到多少柠檬”这样的问题。

短短几个月，从小学数学跨越到了高等数学。

这项来自MIT+哈佛+哥伦比亚大学+滑铁卢大学的联合研究开了什么挂？

对于AI也是审题最重要

研究团队发现以前用AI做数学题的尝试有一个共同点：训练数据里只有文本。

这简直是AI中的文科生，学不好数学也算正常。

那么AI中的理科生要怎么培养？

研究团队的解决思路是先在文本上做预训练，再用代码进行微调。

核心思想是把数学问题转换成等价的编程问题。

他们找来的这位AI理科生与GPT-3师出同门——

OpenAI的Codex，也是GitHub代码生成工具Copilot背后的技术基础。

Codex解题的过程分两步：先审题，再作答。

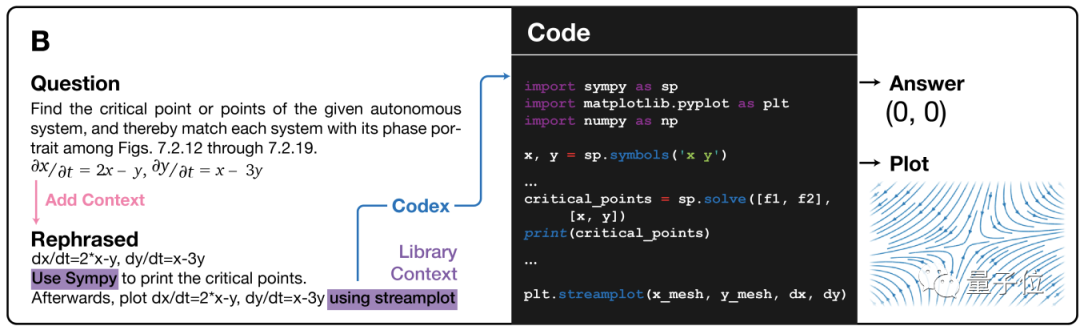
第一步，自动生成需要的上下文，把题干扩充、缩减或改写成适合编程解决的样子。

第二步，生成对应的代码，运行后给出答案。

比如补充自然语言题干中隐藏着的问题语境“在微分方程中”。

列好解题需要用到的Python库。

把问题扩充成更精确的数学语言。

原问题：

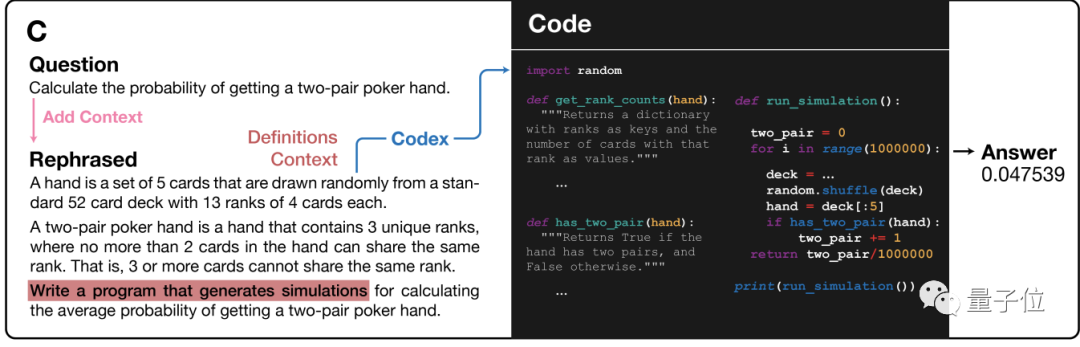
计算扑克牌中一副手牌中有两对的概率。

改写问题：

一副手牌有5张牌，从13组每组4张一共52张牌中随机抽取。
“两对牌型”要求手牌中共有3种牌，每种数量不能多于两张，也就是说相同的牌不能超过三张。
请编写一个模拟程序求出抽到“两对牌型”的概率。

（这也太严谨了）

对于一个复杂问题，先自动生成中间步骤的提示，再写代码。

如果题目中有与数学无关的多余信息，也需要去掉。

就这样，AI靠先审题再写代码的方式做出全部正确答案。

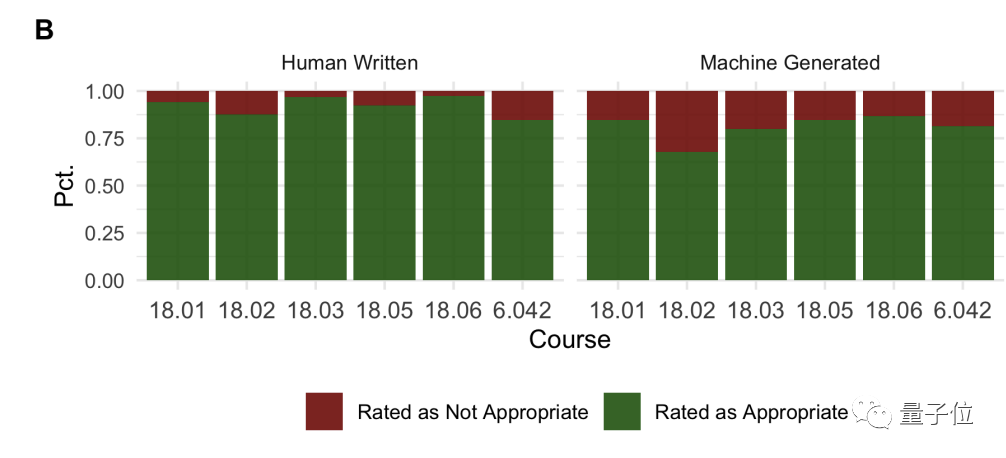
除了做题，学会高数的AI还能反过来给人类出题。

不到一秒钟就能出一道题，试验中总共出了120道题。

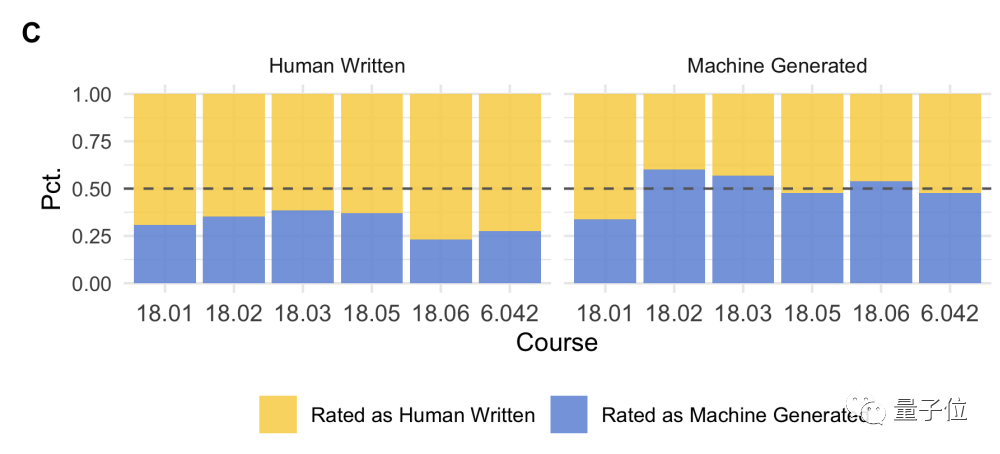
把人类出的题和AI出的题混在一起，找学生来做问卷调查，学生也很难分清一道题是不是AI出的。

他们觉得AI出的题要稍微难一些，但大多数题目放在课程里也算合适。

AI出的题你会做吗？

论文中列出了这项研究还存在几个局限性。

首先是做不了题干带配图的题，这次试验中也没有需要大量证明的题。

另外最终答案是实际运行代码得出的，但最近有研究表明神经网络也可以直接预测出部分代码的执行结果。

以及还是有一些开放性高的题目AI做不出来。

比如“一个向量v能否表示为一个集合S中的向量之和？”或者“以下方程的整数值解是什么？”

最后还有一个彩蛋，论文作者中出现了Gilbert Strang。

他编写的《线性代数导论》被誉为最好的线性代数教科书之一。

他在这篇论文中的贡献是提供了研究思路。

研究团队下一步打算把这项技术扩展到更多课程，并考虑实际应用到教学中。

也许以后MIT的同学期末考试里会有AI出的题了。

要不先来试一试，AI出的题你能做出来吗？

论文地址：
https://arxiv.org/abs/2112.15594

参考链接：
[1]https://www.reddit.com/r/MachineLearning/comments/rutbpv/r_a_neural_network_solves_and_generates/

— 完 —

本文系网易新闻•网易号特色内容激励计划签约账号【量子位】原创内容，未经账号授权，禁止随意转载。

「智能汽车」交流群招募中！

欢迎关注智能汽车、自动驾驶的小伙伴们加入社群，与行业大咖交流、切磋，不错过智能汽车行业发展&技术进展。

ps.加好友请务必备注您的姓名-公司-职位哦~

点这里👇关注我，记得标星哦～

一键三连「分享」、「点赞」和「在看」

科技前沿进展日日相见~