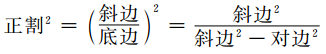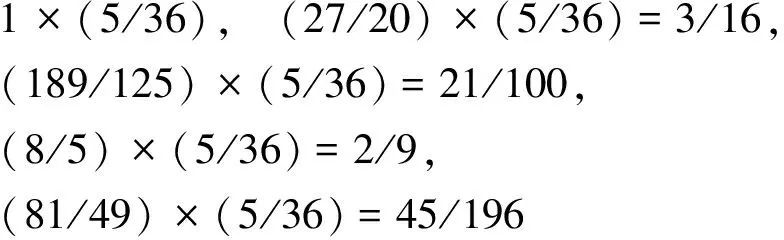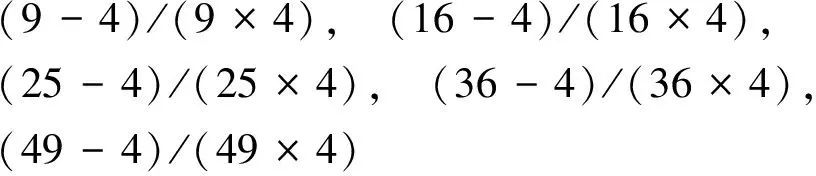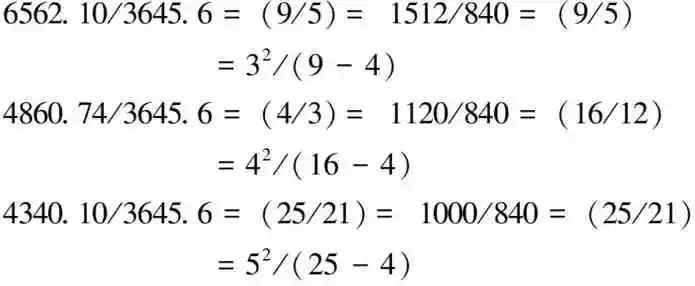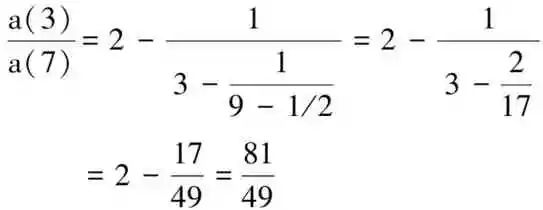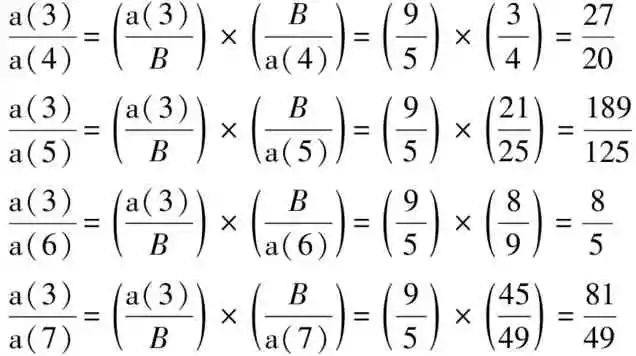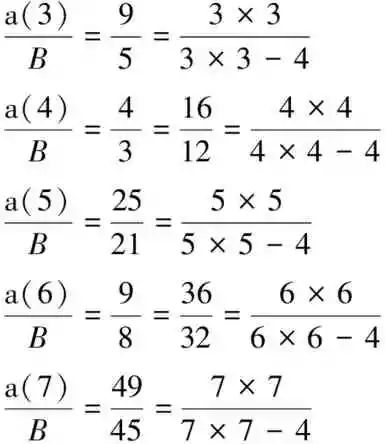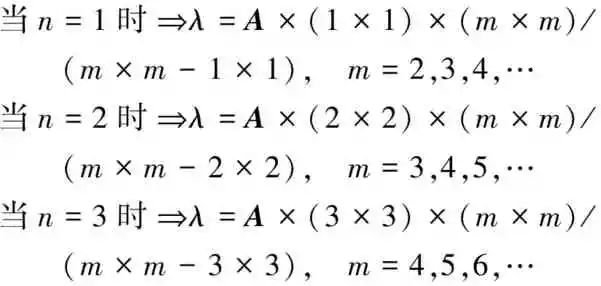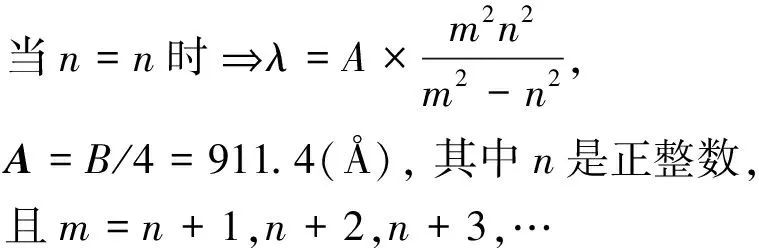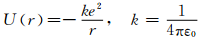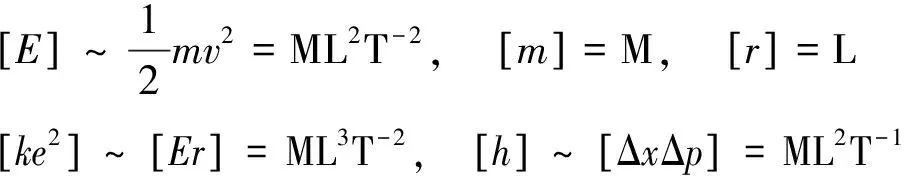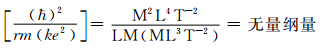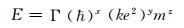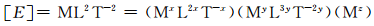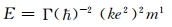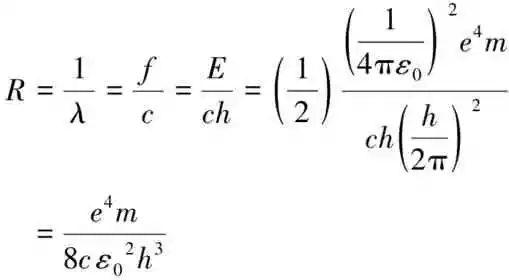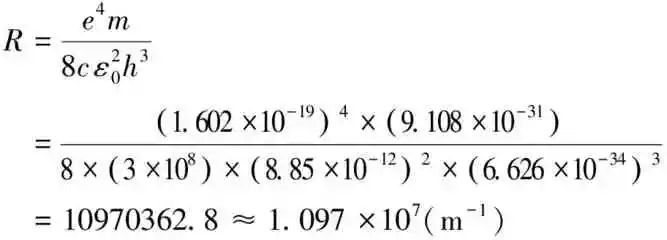以简明物理法重新发现巴耳末公式

回顾近代物理学史，氢原子不连续光谱之巴耳末公式的发现，为原子物理中玻尔理论的创立提供了直接依据，在量子物理发展进程中起了重要作用。当玻尔一看到巴耳末公式，突然间“我都明白这一切了”，这是当时玻尔在与 Léon Rosenfeld会面时所透露的心灵激动[1]。然而，在物理学上从巴耳末的古典时代，过渡到玻尔的量子时代的这一段传奇，其过程疑云重重，始终都无法清晰明白，那巴耳末基数是怎么得来的，这里假设是在巴耳末那个时代节点，不能依靠玻尔理论来推导该公式。

为什么巴耳末基数刚好就是那个数目？由于有关巴耳末基数，这个至关重要的推理线索，至今仍然披着神奇色彩，无法看透又无从捉摸，因当初巴耳末公布经验公式论文[2]中敘述着“从埃格斯特朗的测定，推出这个公式的共同因子是3645.6×10-7mm”，唯独没有阐明巴耳末基数的由来，就这样辗转变成了历史悬案，造成现行基础物理学介绍这一段深具时代开创性的传奇过程时，总是像在梦里求答案就得到了这组数字，然后直接就用这个答案再行推导公式，这在逻辑上有倒果为因推论疑虑，实有碍于物理概念的建立。为了破除这个迷团，消弥学习障碍，有不少人士因此试着提出各种见解，甚至还搬出另一种神奇数字来推导经验公式，但推导手法都不够简明，也欠缺物理图像，这就是为何需要以物理直观进一步探讨的缘由。

本研究方法乃以未知数并运用物理基本概念，于计算不同波长比例时，保留物质元素内稟表征，只要不被约分消掉，其本性自然显露出来，就能推导出经验公式以及推导巴耳末基数，手法一切简明，因果相扣逻辑合理。此外，除了找出巴耳末基数的物理意涵，还要推广巴耳末经验公式，并提出与里德伯公式的等价证明，最后，以量纲分析手法揭露此一内蕴物理量的真正本质。

2 寻找巴耳末基数文献回顾

巴耳末在其论文[2]中没有具体介绍是怎样找到这个共同因子的过程，也就是巴耳末基数。巴耳末经验公式的推导过程不失简单，但不简明，虽然找出了氢原子可见光区光谱线的规律，却失去了找寻巴耳末基数源头的真相。巴耳末本人始终都没有交代是如何精准取得巴耳末基数的推演过程，在当时，此一公式仅止于现象的描述，并未提出此一光谱线背后的成因，氢原子不连续光谱仍然是自然科学界的未解之谜，而巴耳末基数竟成为谜中谜，因此变得富有想像空间。巴耳末基数之谜并非没人打理，也有人试着寻找为什么可以精准取得巴耳末基数。从事科学研究，理应格物致知，本研究乃秉持此一精神。此处先回顾现有寻找巴耳末基数的记载，概分为下列5种：

(1) 沿用巴耳末神奇基数法

这是一般教科书的标准做法，借用巴耳末本人所敘述，直接拿现成的巴耳末基数来用，推导出这些光谱波长的经验公式。至于巴耳末基数的来龙去脉，就把它当历史事件，这留给研究物理学史的学者去琢磨吧。这是目前便宜的行事手法，未来或许因本文而改变。

(2) 以形求数概念式几何法

从几何图形上看到各个谱线就像透视图那样，由近而远，逐渐缩小，就能领悟到谱线波长有迫近某一极值的趋势。以形求数，便成了分析对策，如再细心观察巴耳末公式的数学形式，是不是很像下列式子：

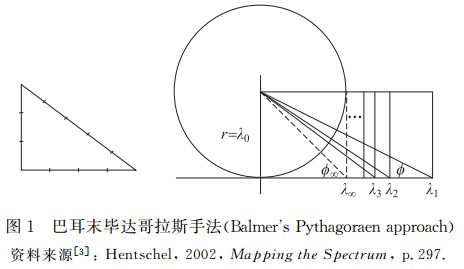
仔细观察上式等号右边的平方比例项形式，与巴耳末公式右边整数平方比例项形式是一模一样，上述公式就是毕达哥拉斯定理的应用，也就是我们较熟悉的勾股定理。由于巴耳末公式当n→∞ 时，λ→B，为这个线系的极限﹐这时邻近二谱线的波长差就趋于零，因而在归纳光谱数据分析手法时，应可将一维问题二维化，于是化学光谱分析专书[3]中采用几何方式，介绍巴耳末光谱分析手法，从几何关系找到谱线波长之间遵循毕达哥拉斯定理(即勾股定理)，经过反复试算，可概念性地找到一个共同因子，就是巴耳末基数，这种以形求数概念就如同下列图1所示。

(3) 以码解数用5/36比例密码法

德国数学家撰写一本《数字巨大的阴影》畅销书[4]，该书内容有一部分是讲玻尔，提到其石破天惊开创原子理论新天地的机遇，就是看了一眼巴耳末公式。在介绍如何推导氢原子光谱公式时，并没沿用迷一样的巴耳末基数，而是运用简单算术，另辟一条路子，尤其要仔细观察各光谱波数比中，若要让分母变化呈现规律，就需在一个5/36比例密码，便可破解氢原子光谱线找出其中规律。其运用简单算术推导过程，也可以当作很好的数据分析入门教材，以下将简约介绍这本书[4]的推演过程，其重点陈述如下：

先取氢原子光谱之波数1523310, 2056410, 2303240, 2437290, 2518130，接着将每一项波数皆除以第一项红光波数，取得各波数比为1, 27/20, 189/125, 8/5, 81/49，注意前述各项分母变化可转为1, 4×5, 25×5, 1×[5], 7×7然后再想办法变成如1, 4, 25, [36], 49这种有规律的数列，重点观察前面两组数列中第四项分母中括号数字，该项分母要同时消掉5又要变成36的话，就得将波数比数列通通都要乘上这个比例密码：5/36，其中，只需用第一项红光波数就能直接算得里德伯常数为：R=1,523,310/(5/36)=10,967,832，然后将红光波数转成里德伯常数与比例密码的乘积再带回到波数比，若将原波数比的分母换成只有里德伯常数的话，则比例密码要挪到等号另一边，也就是将各波数比乘上此密码得到下列数列：

上式中第二项分子分母同乘以4，以及第四项分子分母同乘以16，之后再整理得出下列数列：

仔细整理上式并进一步观察，会发现呈有规律变化的数列如下：

现在重新将上式归纳一下，会得出形如

的规律，再变成倒过来的因子

然后这项是要放到波数等号的右边，于是得到里德伯公式为：

该书中推导氢原子光谱经验公式的关键之处，从观察各波数比中分母变化里看出规律而得到解题灵感，虽说解谜需要奇巧密码之助，却也交代清楚，这个思路虽有一点曲折，推演过程明朗，没有神奇之处，却也未能解开巴耳末基数身分之谜，而其来龙去脉需要数字演练才得以一窥究竟，过程却缺少物理概念。

(4) 以质取数质因数法

若假定巴耳末基数是个公共因子，那么应该能找出氢原子光谱中的公共质数因子，有个网页[5]就是采质因数的因子分析法找出巴耳末基数，其推演过程重点陈述是从红光开始取4个波数1523310, 2056410, 2303240, 2437290，除第一项外，将每个一项波数皆除以第一项红光波数得各波数比27/20=1512/1120, 189/125=1512/1000, 8/5=1512/945，然后从中检列出重要数字1512, 1120, 1000, 945，而这些数字的质因数可表成下列内容：

为这些谱线确定了另一个公共质数因子，其值为23×3×5×7=840，再将4个波数改回4条氢谱线波长分别为：6562.1Å, 4860.74Å, 4340.1Å, 4101.2Å，于是从红光波长可求得公共因子数值为6562.1/(1512/840)=3645.6，就这样找到了巴耳末基数，至于巴耳末公式，可从4条氢谱线波长比转成质数因子比，特征是分别除以公共因子，公式就得以推导，其过程如下：

将前4个算式稍加整理就能得出巴耳末公式：

其中B=3645.6,n=2,m=3,4,5,6。

质因数因子分析法能找出神奇基数，是对数字具有洞察力，或许有一点运气，不能一般性推广，总之，这也是个没有物理概念的数字游戏，于通俗物理介绍可用，但于正式基础物理课程却不宜。

19世纪开始不断涌现出各式各样的光谱实验，吸引物理学家注意并试着解析此现象，但流于习惯用力学思维方法，始终摆脱不了旧物理框架束缚，光谱线问题难倒了众多科学家。也许正是这个因素，在光谱规律上的研究，首先打开突破口的不是物理学家，而是瑞士的一名中学数学老师巴耳末，当时年届60的他，受到对光谱很有研究的物理教授哈根拜希的鼓励，试图寻找氢光谱的规律。由于光谱线不连续的特征是隐藏在比例项形式的数，而分数形式间变化规律的掌握，恰恰是数学家的强项(前面就有两个实例)，而且巴耳末对建筑结构、图形透视、几何素描有浓厚兴趣，专长是投影几何，写过这方面的专书，他在数与几何方面的特长使他取得了物理学家没能做到的成就。巴耳末公式是由其基数乘上分数形式比例项所构成的，这看似平常，因而没引起后续物理学家的高度关切，直到玻尔看了一眼，玻尔看对眼的并不是其基数，而是比例项的分数形式与所搭配的整数递变规律，那可是玻尔建立模型所需稳定态能级跃迁假设的灵感泉源。

当回顾前述对巴耳末基“数”解谜之文献，有世说角度，以事讲数；有从数学角度，找比例因子以码解数，或寻质数因子以质取数；也有光谱分析角度，以形求数；唯独没有从物理角度，以理导数，这就是本研究的契机。

3 回顾氢原子光谱简史并提出假设及拟定研究方法

这里特别把有关氢原子光谱的个案历史拿出来谈，以便聚焦吸收知识，也方便后续的探索。1814年，夫琅禾费发明了分光仪，并在太阳光的光谱研究中发现了574条黑线，这些线被称作夫琅禾费线。1853年埃格斯特朗首先发现氢原子光谱线，但测量不易，由于不是用气体放电管，而是常压下利用电火花放电法研究，观测虽有所发现，但激发的原子生命非常短暂不易测量。1862年用早期颈部肥大圆柱管状的盖斯勒管，他在研究气体放电中，确认了氢原子的Hα线(6562.1Å)，即红线谱线，随后证明它就是夫琅禾费在太阳光谱中发现的C线。之后又发现氢原子3条在可见光区域内的光谱线，即Hβ线(4860.74Å)、Hγ线(4340.1Å)、Hδ线(4101.2Å)。现在做历史场景的模拟，假设吾人是回到19世纪的物理学家，那个年代通讯不发达，科学家大都靠私交书信流通科学新知或发现，如果吾人当时并不知道有一门光谱分析学，又前述氢原子光谱线是在地球上找到的，然后埃格斯特朗核对此前先有的太阳光谱，从中发现其C线暗条位置与氢原子光谱完全重合，这才发现，原来太阳大气中存有氢原子。单单得知这道重要巧合讯息，就当代的时空背景与科学知识条件，作为基础科学的研究精神，可以大胆地提出两点假设：第一假设：氢原子激发不连续光谱线只与原子的内蕴(intrinsic)物理量有关；第二假设：氢原子不连续光谱线波长就是此一内蕴物理量的特定表征。

虽然我们不了解原子的内蕴物理量，由第二假设可以知道，当同一原子不同光谱线波长求比值时，由于其特定表征都会同时出现在分子项与分母项中，因此，如果将氢原子发出不同光谱线波长两两相除的话，会对其内蕴物理量之外在表征做约分被消除掉，而无法察觉内蕴物理量的存在。如若想掌握其内蕴物理量之特性表征，就必须在求波长比时，不能让它被约分而不见踪迹，自然就会显露其物理量面貌，以下就是要落实这个思路的最简单做法。

首先令氢原子有一不为零之未知内蕴物理量定为参数B，然后将它同时乘上波长比的分子项与分母项，接着转换成各带一个参数B并分立成两项分数的乘积，以如下公式说明会更明白：

再来就看看有没有机会，就前后两项各拥一个B参数的分数是否有规律可循。事实上，从前面的历史回顾与探索思路，应能推断B参数与经验公式都是同时存在于波长间比例关系式中，因此可以不用先管参数B，就能从波长间比例关系式中推导出经验公式，换句话说，这里暂时不知道B参数的切确数值，试着不靠参数B值来找寻发现经验公式的途径，这个做法与所有文献做法全然不同，当然也不同于巴耳末的做法。

4 推导巴耳末经验公式

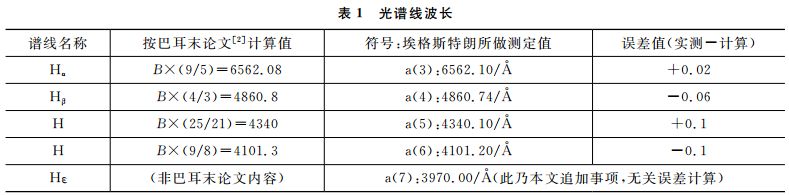
由于不知道当时巴耳末分析数据的误差是什么情况，其采用分数比例形式计算出来的波长真的可信吗？这里得先做公式计算与实际测量的误差计算，倘若误差不能接受，那么巴耳末公式就不值得深究下去了。考虑原巴耳末取材自当时氢原子光谱在可见光区波段早被埃格斯特朗测定的4条谱线波长数据，再经巴耳末公式计算并进行与实际测量的误差计算，详如表1所示，可以发现误差小于波长的

吻合得十分出色，因此有信心深入探索。又为了增加数据分析的难度，另再追加一条谱线波长数据，总共拿这红、青绿、青、蓝、紫等5色氢原子光谱谱线波长，并以符号化为各项光谱线波长命名如表1所示。

首先列出最长波长与其他波长间的比值与近似的整数比例关系计算如下：

a(3)/a(4)=1.35002078,比值取小数点后三位并经四舍五入得1.350=27/20,

a(3)/a(5)=1.51196977,比值取小数点后三位并经四舍五入得1.512=189/125,

a(3)/a(6)=1.60004389,比值取小数点后三位并经四舍五入得1.600=8/5,

a(3)/a(7)=1.65292191,比值取小数点后三位并经四舍五入得1.653=…？

最后一项比值不能很快算出其整数比例式，由于所有实数皆可将它展开成为简单连分数，我们可以借助相同概念，从这个思路出发，不需要大海捞针，但需要一些步骤，进行比数分解成形式类似简单连分数以找出近似的分数。步骤是这样的，辗转运算过程是先同时将分母与分子都经放大10倍以去除小数点，即a(3)/a(7)=1.65292191=65621/39700，计算波长比例是采长波长除以短波长的比数，结果能很快找到一个2的整数下限，使得a(3)/a(7)=2-(2×39700-65621)/39700=2-13779/39700，再将分数项倒转过来形成39700/13779=3-(3×13779-39700)/13779=3-1637/13779，再运用同样的辗转运算手法，又将分数项倒转过来形成13779/1637=9-(9×1637-13779)/1637=9-954/1637，令分数项954/1637取近似值为1/2，则13779/1637=9-1/2，因此重新整理表成減号的简单连分数形式，此一完整计算过程如下：

这个近似分数到底能不能接受呢？现在验算一下其数值结果为a(3)/a(7)=81/49=1.653061，虽然符合近似值为1.653的要求，还是再回头用原始波长比值为a(3)/a(7)=1.652922，验证发现十分逼近用原始波长计算的结果，这个近似分数是可以接受的。重新整理波长比例关系如下：

重点现在就要让内蕴物理量参数B重返公式，不要被除时而消去掉，具体做法就是将此参数分别乘上前述各式以波长代号的分母项与分子项，其整数比例关系并不会因此而改变，然后将前述各式中间等号左边之符号比例项经适度调整并分立成两项比例的乘积，同样思路也用在前述各式中间等号右边之整数比例项，经适度调整也分立成两项比例的乘积，整个推演计算过程重新整理成新的关系式如下：

综观上述4组比例式的前后关系式子，对照分立中间等号两边的两个波长代号比例乘积与两个整数比例乘积，呈现出一对对小括号比例因子的乘积，很容易发现其前项乘数共同因子都长得一模一样，也就是，中间等号左边波长代号比例共同因子是a(3)/B，而右边整数比例共同因子则是9/5，然后将中间等号两边两两相对映的其他小括号因子找出来，再经过整理符号与整数比例间之一一对映，就能得出下列5组符号整数比关系恒等式的数列：

这些公式中只有参数B是个未知参数，此外都是已知数值，而且各项公式之形式都是一个未知数一个方程式，这是最容易求解的。显而易见，因为没有约分消掉，所以本性就显露出来，这就是当初分析思路的目的，但这里先暂时不算，以便凸显接下来要进行的重点工作，要在参数B完全不知道的切确条件之下，也能推演出巴耳末经验公式。

上述恒等式中，除了头一项保持原状以外，将其他恒等式的分母与分子上下对调一番，全数恒等式变成如同头一项形式一样，皆是以参数B为分母的符号比等于整数比的数列：

初看起来，这5项整数比像似无法构成规律性的分数数列，但如果将第二项和第四项之分子与分母分别乘以4，接着进行建立平方项推演，则分子部分依序可书写成3×3，4×4，5×5，6×6，7×7，而分母部分相应书写成完全平方再減4，这样就出现了依序渐增平方的变化规律。重新整理新得到的符号整数比恒等式如下列所示：

在不知参数B 切确数值条件之下，从这些符号整数比恒等式的渐增平方规律，很容易从前5个式子归纳出巴耳末经验公式如下：

5 推算巴耳末基数

巴耳末基数皆出现在一元一次方程式的符号整数比关系恒等式中，因此采用任何一个已知波长并借由前述关系式就能很快求得巴耳末基数切确数值，但分数也是近似值，因此分别求出之后再取平均值，又为了与已知巴耳末基数做对照，这里先剔除先前额外加进来的最末项，取前四项同巴耳末所选用的波长当计算依据，计算过程如下：

由于每个分数都是近似值，取平均值得B=3645.59，如与巴耳末一样取小数后一位的话，那就得到一样的数值：3645.6，终于这般如此容易，巴耳末基数现身了。

6 推广巴耳末公式并证明与里德伯公式等价

由于巴耳末公式起初预测氢原子的其他光谱线系列波长不准，势必要修正，光谱研究方面，巴耳末脚步并未停歇，持续于1897年发表另一篇论文“光谱波长的一个新公式”[6]，巴耳末自己也在该论文中提出修正，也就是将原巴耳末基数除4得A=B/4=3645.6/4=911.4Å，这个新修正过的A值，就是我们于前述第二项假设的内蕴物理量，但为何出现4这个数字？又为何刚好是整数？有必要探讨了解。由于该值是2的平方，马上联想到与比例平方项式有关联的，重新整理后，可以发现是规律变化的一部分，现在试着计算一下不同的n值并查验一下变化规律，试算过程如下：

通过前面试算过程，可看出当n=2时就是原先的巴耳末公式，现归纳推广后的巴耳末经验通式：

此乃巴耳末经验通式，适用于所有的氢原子光谱线系，终于求得氢原子内蕴物理量A=911.4Å，这个攸关第二项假设内蕴物理量的存在性已经证明了，但为何是这个值呢？此值的成因要如何解释，至于比例关系项里头的m与n参数各有何物理意义？又为何刚好都是整数呢？要回答这个问题，光靠经验公式这种唯象理论是不行的，得深入发展理论架构才行，因此就要靠物理发展史接下来的玻尔氢原子模型理论进行探索，才能揭露前述唯象理论有关困惑，这已超出研究范围故不做探讨。

接下来就是证明这个推广后的巴耳末经验通式与里德伯公式是否等价，当然对象局限于氢原子。首先要进行波长换成波数的表示式，只要将推广后的巴耳末经验通式之分子项与分母项上下对调，就能转成里德伯公式，显然这就构成了它们之间的等价证明，这里用最后修正的巴耳末基数来计算出R=1/A=1/911.4=10972130.79m-1，这个数字接近里德伯当年所提的常数值10970000m-1[7]。推广后的巴耳末经验通式与里德伯公式的等价证明推演，十分简单，但限于氢原子所有光谱系，只要进行求波长倒数换成波数的表示式，过程详如下列形式转换：

7 以量纲分析揭露内蕴物理量的本质

虽然此前已推得里德伯常数R的真正数值，可是只能假定它是一个属于氢原子的内蕴物理量，却不清楚它是由哪些基本物理常数所构成，因此，本单元将以量纲分析手法[8]揭露此一内蕴物理量的真正本质。此处选取质量(M)、长度(L)、时间(T)3个基本量纲，就氢原子中一个电子受库仑力吸引绕着以原子核为中心在半经r处做圆周运动来进行量纲分析。首先考量此一由库仑力产生的势能：

现就上述位能公式中找出一些有兴趣的物理量，以及考量海森伯不确定度关系，并按照它们与基本量之间的关系式道出下列分析所需的各种量纲式：

仔细研究上述各种量纲式，可得到一个无量纲量(学巴耳末没做交代，欲知过程详见文献[9])如下：

由于我们是在探讨此一系统的内蕴物理量，而上述无量纲量中的r是个变量而不是常数，因此把它剔除，这样就符合本研究的第一项假设，此时，由于式(1)少了半径，这相当于是把式(1)的无量纲量乘上一个长度基本量纲，就会变成一个具长度纲量的内蕴物理量，其量纲又等同于巴耳末基数，于是也会有着巴耳末基数的内蕴作用，也就是会按本研究的第二项假设来运作，因此这个式(1)少了半径的物理量会隐藏在氢原子所发射的光波之中，所以，该光波所具有的能量E会是由上述式(1)无量纲量中除开半径以外的其他3种不同道出量所组成，接着针对这些道出量分别设置相对应的量纲指数x,y,z，并存在一个未知比例系数Γ，使得能量E与这些道出量的函数关系式如下：

那么可以从上述式(2)可得到能量的量纲式为

就量纲的一致性对照上式不同基本量纲其已知与未知之间的量纲关系，可分别找出下列联立方程组：

对上述代数方程组求解，可得3个量纲指数分别为x=-2,y=2,z=1，再把它们代回到式(2)，使得能量E与这些道出量的函数关系式如下：

又里德伯常数的量纲是波长λ的倒数，此光量子能量为E=h f，其中f为其频率，并令式(3)函数关系中的系数Γ=1/2，再把这些与式(3)关联起来，于是能道出由基本物理常数实际构成的里德伯常数：

今分别引用物理基本常数：电子的荷电量(e)=1.602×10-19C，电子质量(m)=9.108×10-31kg，光速(c)=3×108m·s-1，真空介电常数(ε0)=8.85×10-12C2·N-1·m-2，普朗克常数(h)=6.626×10-34J·s，将这些物理常数代入到式(4)中，可算得其数值如下：

上述经相关物理常数计算值，以及前一单元自创新法里对实验波长数据所做的里德伯常数R推算值，都和当年能被大家接受的四位有效数字的值[7]完全一致，因此，本研究要找的内蕴物理量，其本质内涵就是经量纲分析所得里德伯常数的式(4)里所用基本物理常数关系式，这也与玻尔理论所推得的形式及内涵完全一致，至此，也验证了本文于进行研究前所做的两项假设事项。

8 结论

课堂上没讲清楚的巴耳末公式，除了数学家还有一些余热之外，就只剩记忆里的历史片段了，何曾想到，深入研究发现，竟能用如此简明的物理推导手法，就能重新发现巴耳末公式，并以量纲分析及沿用本研究的两个假设，就能揭露光谱线中内蕴物理量的真正本质！现总结一下研究心得：

(1) 用多元角度数据分析刺激建模灵感。本文保留了各路对解決巴耳末公式的不同推演手法，用意是提供课堂上数据分析的多元角度练习，借由不同手法推论特征，从而体认到数学家与物理学家在解決问题层面会有本质上的不同，希望能从这些素材刺激一些灵感泉源。本质上，物理理论都是简化复杂面貌后的浓缩资讯，单从理论学不到全貌，其根本原因是，建模者原来综观问题核心的思量，原创者建模的拿捏过程，这些林林总总如何促成建立模型的重要养份没有教，也是无从教起的，至今没人完全知道哥白尼、开普勒、牛顿、玻尔、爱因斯坦等人怎么能够觉察问题，找出问题的关键所在，进而发明自己的创见。这些无价之宝，乃是研究层面的真学问，只能当它是灵感吧！

(2) 创造力=创造另一种可能。本文所用资料背景和巴耳末所处年代完全一样，就是为了在教学过程中，除了能以历史轨迹讲授当代科学发展史与巴耳末公式的特殊贡献之外，还能以不一样的逻辑轨迹用随堂方式演练历史的偶然，因为学习物理也需学习创造力，而创造力就是创造另一种可能，理应研习在一些偶然情况下做出不一样的假设条件，从而进行创造性思考与推理，如此场景在外、思路在内相互呼应，以内外兼有的物理图像，期建立学子清晰的物理概念。

(3) 铺垫物理发展三部曲。杨振宁[10]针对物理界研究定性地概分为实验物理、唯象理论和理论架构三部分。先从哥白尼日心说讲起，经过开普勒创建三大定律，然后这些成果奠定了牛顿的万有引力定律。以上体现古典物理的实验物理、唯象理论和理论构架三部曲，这一路发展充满了物理图像。反观近代物理史发展，从氢原子光谱的实验物理，过渡到巴耳末公式的唯象理论，再到玻尔氢原子模型理论，这是课堂必上教材，然而在教授巴耳末公式时，往往采讲故事的方式带过，问题是，没有了物理量方面实际操练，就易失去对物理性质的感受，这一避重就轻的弯道超车，会让认知披上一层神秘面纱，造成学习上的一个断层现象。本研究找到了巴耳末公式所欠缺的最后一块物理拼图，从而清楚认识其来龙去脉，再佐以量纲分析，能顺势与玻尔模型接轨，过程思路就清晰了，这一路发展才又充满了物理图像，进而完备了近代物理史发展的实验物理、唯象理论和理论架构三部曲。

(4) 逆向思考切入问题的隐因还原比例法。固有成见常会潜意识地自我设限，框住了自己创建发现的开拓潜力，要如何摆脱，将成为科学家的重要养成教育。其中有个办法就是逆向思考，在物理史中有个典型的例子，就是费米灵机一动拿石蜡做实验意外发现了慢中子效应。一般人在进行比例计算，当分子分母有相同乘积项时，都会进行两两消除。本研究所探明的一种简易且具物理直观方法，也是采用逆向思考，将一般计算比例思路反过来，把被隐藏具物理意义的重要因子，当作共同乘积项，借由比例计算将其还原到分子分母里，因此，特将此研究方法称之为隐因还原比例法。至于本方法相关的理论介绍，与量纲分析又有何关联，可参考接续本研究发展的下篇文献[9]。

[1] HEILBRON J L. Historical studies in the theory of atomic structure[M]. New York: Arno Press Inc. 1981: 265.

[2] BALMER J J. Notiz über die Spectrallinien des Wasserstoffs[J]. Annalen der Physik, 1885, 25: 80-87.

[3] HENTSCHEL K. Mapping the spectrum[M]. Oxford: Oxford University Press, 2002.

[4] TASCHNER R. Der Zahlen gigantische Schatten (3. Auflage)[M]. Wiesbaden: Vieweg Verlag, 2005: 137-143.

[5] BROWN K. (2007). The hydrogen atom. MathPages. Retrieved Oct. 7, 2012, from http://www.mathpages.com/home/kmath538/kmath538.htm.

[6] BALMER J J. Eine neue Formal für Spectralwellen[J]. Annalen der Physik, 1887, 60: 380-391.

[7] FRENCH A P, TAYLOR E F. An Introduction to quantum physics[M]. New York: W. W. Norton and Company, Inc. 1978: 16.

[8] 赵凯华.定性与半定量物理学[M].北京:高等教育出版社，1991.

[9] 邓崇林.创新量纲分析重道玻尔模型能级公式[J].物理与工程，2019，优先出版.

TENG C L. Using New approach in dimensional analysis to reform the formula for the Bohr model’s energy levels[J]. Physics and Engineering, 2019, online first.

YANG C N. Beauty and physics[J]. Twenty-First Century, 1997, 40(4): 71-79. (in Chinese)