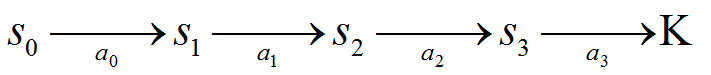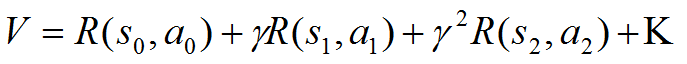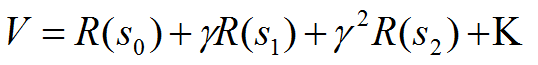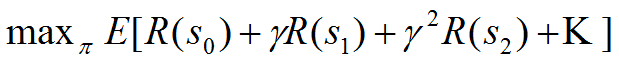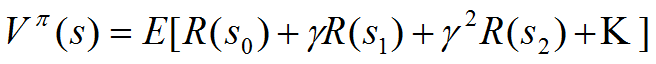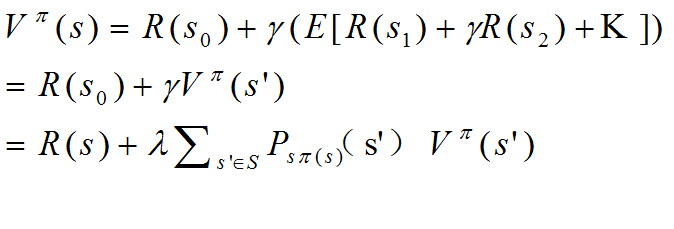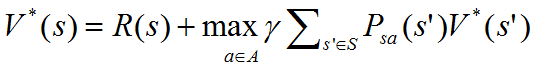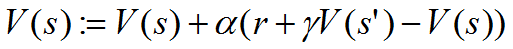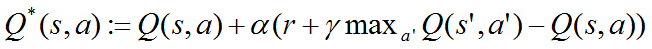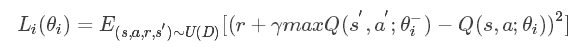论文笔记:利用深度加强学习达到人类的控制水平
原文题目:Human-levelcontrol through deep reinforcement learning
原文链接:https://www.nature.com/articles/nature14236
源码地址:https://sites.google.com/a/deepmind.com/dqn
实验视频:http://v.youku.com/v_show/id_XODk5OTQxMDk2.html
这是一篇2015年的nature,需要对深度学习与强化学习有一定的认识基础再来读这篇paper。DeepMind的AI的设计核心是如何让计算机自行发现数据中存在的模式。其解决方案是深度神经网络与强化学习等方法的的结合。AI并并不知道游戏规则,而是用深度神经网络来了解游戏的状态,找出哪一种行为能导致得分最高。尽管利用模拟神经网络来教电脑玩游戏(如军棋游戏)的方法已经使用了几十年,但是从未有人能像DeepMind团队那样以如此有用的方式结合到一起,其方案展现出了令人印象深刻的可适应性。但我还是觉得这篇文章太难了,所以准备了一些相关基础知识。
强化学习:
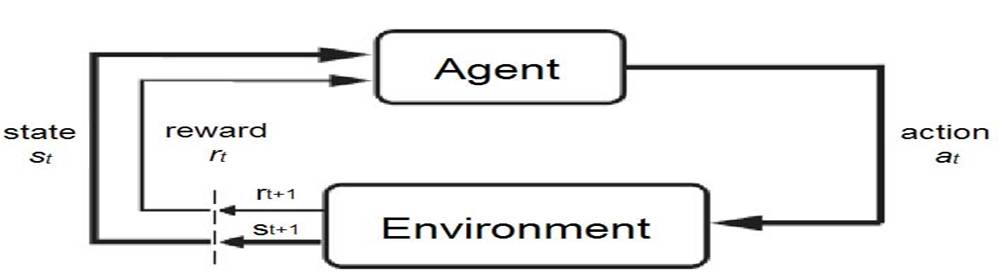
强化学习就是agent(又称智能系统或智能体)通过与环境的交互学习一个从环境状态到行为映射,学习的目标是使其累积折扣回报值最大。传统的强化学习依赖于组合人工特征和线性价值函数(value function)或策略表达来实现。
马尔科夫决策链:
马尔科夫决策过程一般包含如下五个元素:
1. 状态集s。比如,在物体位置坐标。
2. 动作集A。比如,执行上下左右等一系列可行的动作集。
3. 状态转移概率Psa。 Psa表示在状态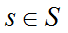
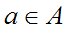
4. 阻尼系数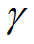
5. 回报函数R, R:SxA→R,表示当前状态下执行某个动作能得到的回报值。
马尔可夫决策过程:
agent的决策过程如下:
2. 计算总的回报值V:
3. 如果回报函数R只和状态S有关而与动作无关:
4.我们选择一个最佳的策略使得回报最大:
5. 定义值函数V为在当前状态s下执行策略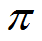
6. 我们将上式表示为当前回报和后续回报的形式:
7.假设有一个最优策略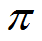
•这就是一个Bellman等式的形式
Q-learing算法:
1、Sutton's TD(0)算法:这个算法一样会考虑当前回报和下一状态的估计值,它的更新公式如下:
其中公式右侧的V(s)是V(s)的旧值(值迭代的过程), 是学习效率。
2、Q-learing算法:它和Sutton's TD(0)算法类似,只是将动作集A也考虑进来。定义动作价值函数Q(s,a),Q-learning的更新规则:
深度强化学习(DRL)
将深度学习和强化学习结合在一起,直接从高维原始数据学习控制策略。具体是将卷积神经网络和Q Learning结合在一起。卷积神经网络的输入是原始图像数据(作为状态)输出则为每个动作对应的价值Value Function来估计未来的反馈Reward。
但是结合二者是有困难的,具体表现在:
(1)深度学习的成功依赖于大量的有标签的样本,从而进行有监督学习。而增强学习只有一个reward返回值,并且这个值还常常带有噪声,延迟,并且是稀少的(sparse),理解是不可能每个state给个reward。特别是延迟Delay,常常是几千毫秒之后再返回。
(2)深度学习的样本都是独立的,而RL中的state状态却是相关的,前后的状态是有影响的,这显而易见。
(3)深度学习的目标分布是固定的。一个图片是车就是车,不会变。但增强学习,分布却是一直变化的,比如超级玛丽,前面的场景和后面的场景不一样,可能前面的训练好了,后面又不行了,或者后面的训练好了前面又用不了了。
DQN算法:
DQN=CNN +Q-learning
(1)通过Q-Learning使用reward来构造标签
(2)通过experience replay的方法来解决相关性及非静态分布问题
因为输入是RGB,像素也高,因此,对图像进行初步的图像处理,变成灰度矩形84*84的图像作为输入,有利于卷积。 接下来就是模型的构建问题,毕竟Q(s,a)包含s和a。一种方法就是输入s和a,输出q值,这样并不方便,每个a都需要forward一遍网络。
Deepmind的做法是神经网络只输入s,输出则是每个a对应的q。这种做法的优点就是只要输入s,forward前向传播一遍就可以获取所有a的q值,毕竟a的数量有限。
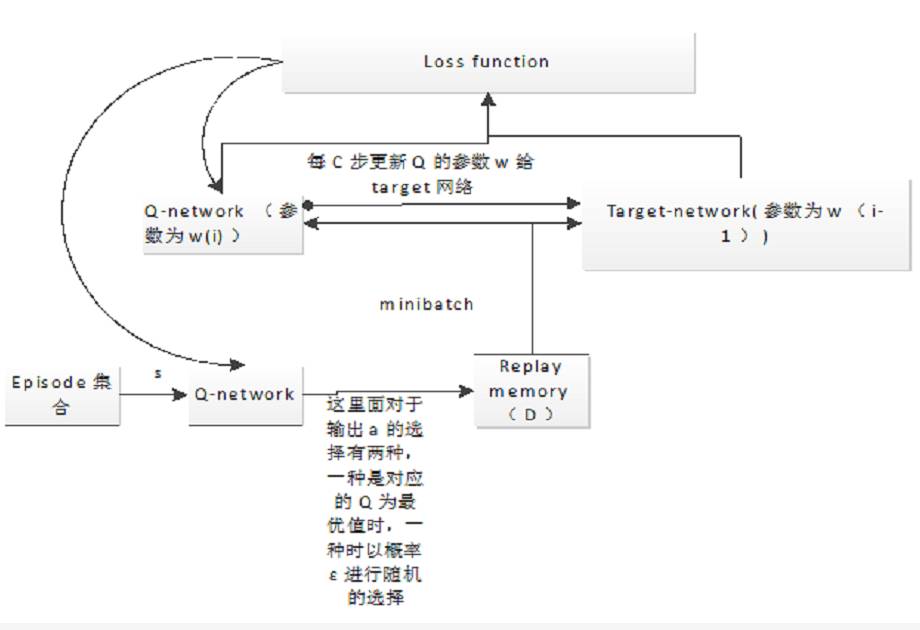
算法框架:
摘要:
强化学习理论来源于于心理学和神经科学,它可以规范性解释一个Agent如何在一个环境中优化自己的控制。为了在真实复杂的物理世界中成功的使用强化学习算法,一个Agent必须面对困难的任务:利用高维的传感器输入数据,达到很好的表达,并且泛化之前的经验到新的未见环境中。显然的,人类和其他动物通过协调的组合强化学习以及层次化的感知处理系统来很好的处理这个问题。前者已经被大量的神经数据证明了,揭示了在多巴胺能的神经元激发的相位信号和短时差分强化学习算法。现在强化学习算法已经在一些领域取得了成功,然而它之前在那些手动提取有用特征的领域、或者一些低维可以直接观察到的领域受到了应用限制。这里我们使用最近先进的手段训练深度神经网络类得到一个,名字叫Deep Q-network的算法,它可以使用end-to-end强化学习算法从高维的传感器输入中成功的直接学习到成功的策略。我们在具有挑战性的游戏Atari2600中测试了这个Agent。我们证明了,使用同一种算法和网络,同一种超参数,在49种游戏集合中,仅仅使用像素点和游戏分数作为输入,超过以往的任何一种算法达到和以及实现了专业游戏玩家的水平。这个工作在高维数据输入和动作输出之间建立了桥梁,使得人工智能Agent可以达到擅长一系列的挑战性的工作。
贡献及结果:
构建一个全新的Agent,基于Deep Q-network,可以直接从高维的原始输入数据中通过end-to-end的增强学习训练来学习策略。将算法应用到Atari 2600 游戏中,其中49个游戏水平超过人类。第一个连接了高维的感知输入到动作,能够通用地学习多种不同的task。
困难:
使用深度卷积神经网络来近似最优动作-状态函数。但是,使用非线性函数近似器比如神经网络来近似动作-值函数时,强化学习会不稳定甚至出现偏差甚至发散。很大的原因在于数据之间的相关性太强,Q值的微小变动会很大地改变策略,从而改变数据分布,改变动作值(Q)与目标值r+γmaxa′Q(s′,a′)之间的关联性。
解决方案:
1.使用experience replay来打乱观测值之间的相关性,平滑数据分布的变化。
2.将目标Q值的参数周期性更新,目的为减小Q值与目标值之间的相关性。
我们使用深度卷积神经网络来近似值函数Q(s,a;θi),其中θi是迭代第i步的神经网络参数。对于experience replay,我们在每一个时间步t存储经验et=(st,at,rt,st+1)到一个数据集Dt=e1,⋯,et中。进行学习的时候,我们从经验中随机抽取样本(s,a,r,s′)∼U(D)进行Q-learning更新。在第i次迭代中,Q-learning更新使用如下的损失函数:
其中,γ是折扣因素,决定智能体的视野,θi是第i次迭代时Q-网络的参数,θ−i是第i次迭代时用于计算目标值得网络参数。目标网络参数θ−i每隔C步用Q-网络的参数θi来更新,期间保持不变。
借用Atari游戏平台(49种游戏)来验证算法。使用相同的网络结构,相同的超参数值,和相同的学习程序,(输入高维数据210×160的彩色录像,60hz),来证明我们的方法在不同的平台下都鲁棒地学习到了成功的策略。
处理方法:
算法流程:
1)初始化replay memory D,容量是N用于存储 训练的样本
2)初始化action-value function 的Q 卷积神经网络 ,初始的参数θ随机
3)初始化 target action-value function的卷积神经网络,结构和Q的一样,参数θ∗−初始等于Q的参数
Preprocessing:
算法直接处理Atari游戏的裸数据,一帧是210×160个像素点,128色,数据量非常大,对计算能力和记忆存储量提出了很高的要求。我们提前进行预处理是为了减低输入量的维度和对Atari仿真器进行一些处理。
1.对单帧进行编码,对每个像素的颜色值取最大值(在已编码的帧和之前的帧中,比如m帧,m=4,3,5都可以),这样可以消除由于闪烁造成的部分图像的缺失。
2.从RGB帧中提取Y通道的数据(即亮度数据)并重新调整为84×84的数据。
Model architecture
我们使用的结构是,输入状态,输出该状态下每个动作的Q值。
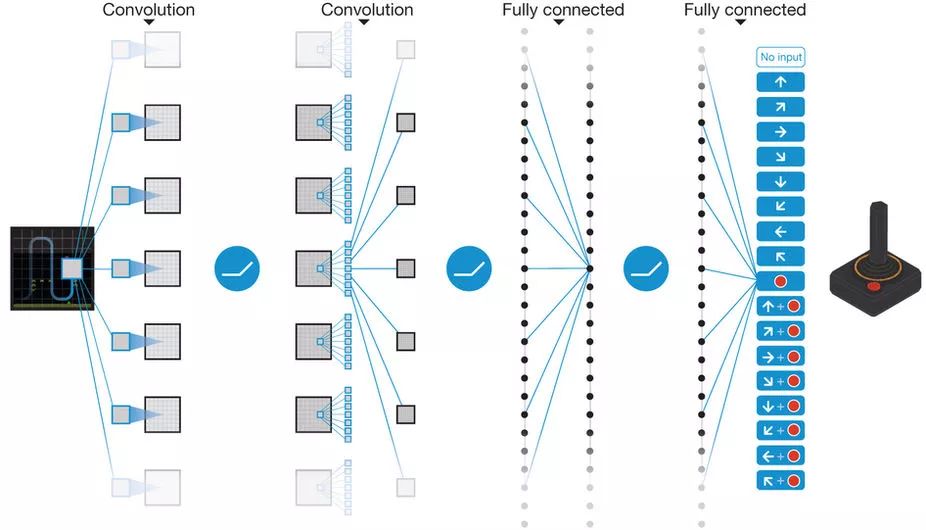
结构图如图1所示。其中神经网络的输入是由预处理之后的结果—84×84×4的图像;第一层隐含层包括32个8×8的滤波器,步幅是4,后面跟一个非线性整流器(a rectifier nonlinearity);第二层隐含层包括64个4×4的滤波器,步幅是2,后面加一个非线性整流器;第三层隐含层包括64个3×3的滤波器,步幅是1,后面跟一个整流器;最后一个隐含层是全连接,包含512个整流单元;输出层是线性全连接层,输出的个数是action的个数。
Figure 1: Schematic illustration of the convolutional neural network
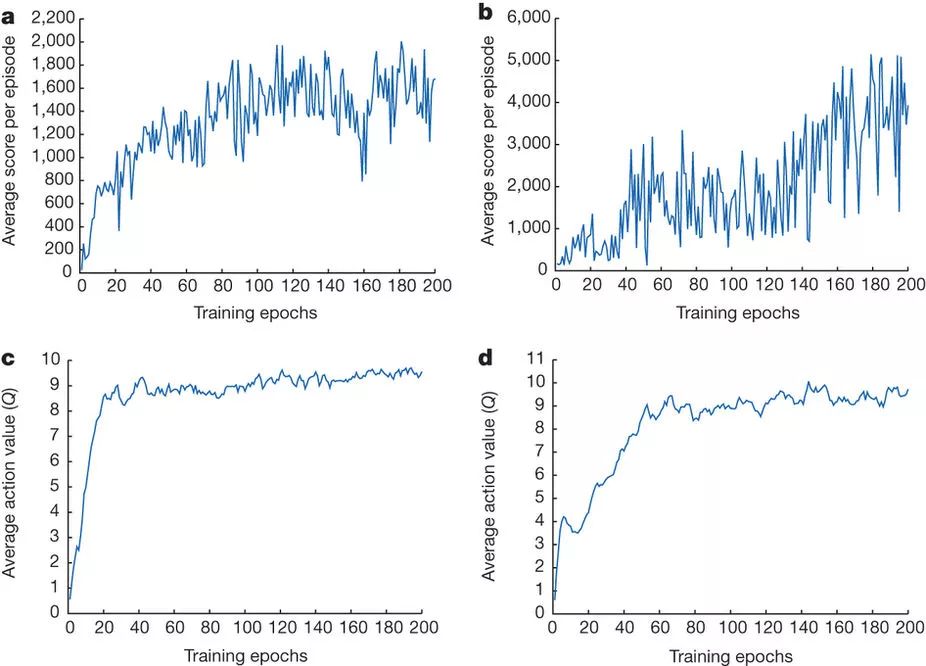
Figure 2: Training curves tracking the agent’s average score and average predicted action-value.
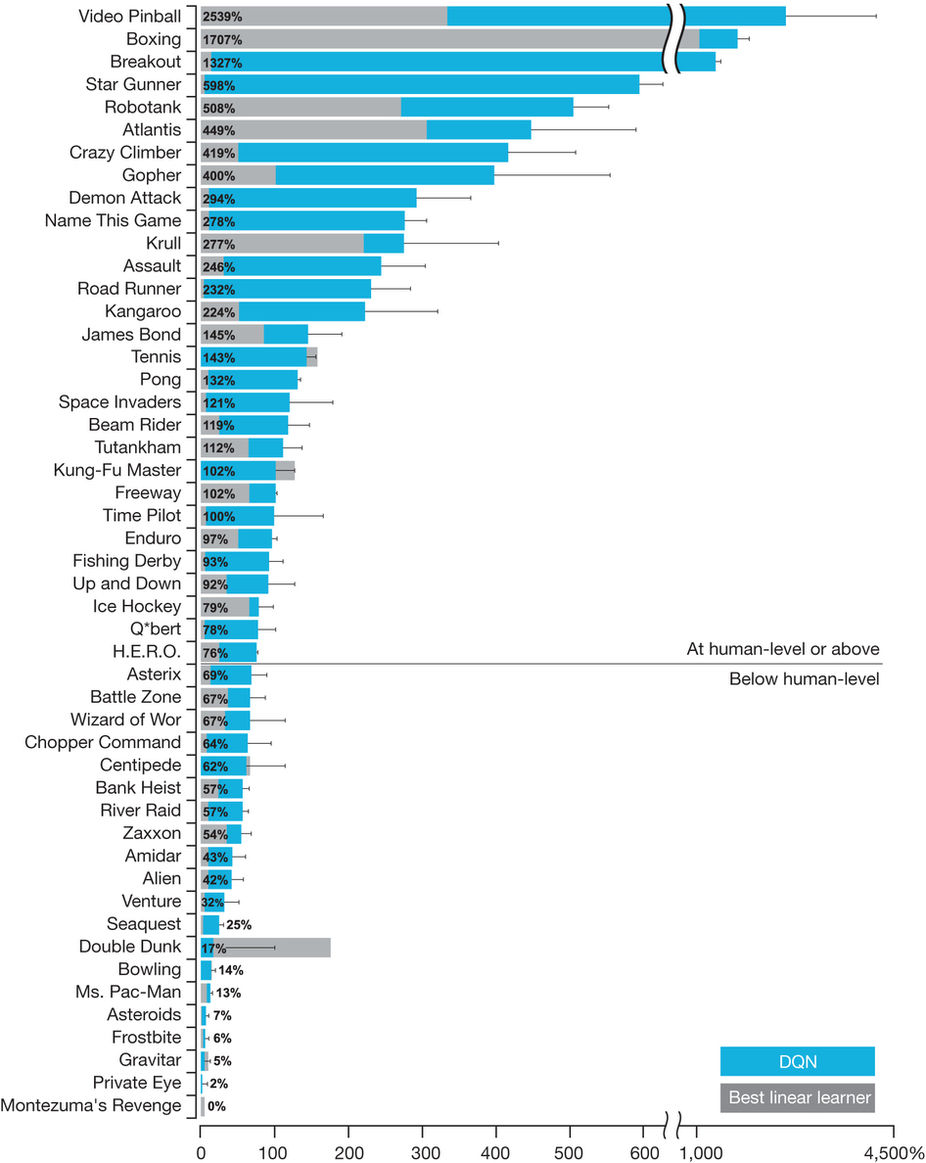
Figure 3: Comparison of the DQN agent with the best reinforcement learning methods15 in the literature.
Training details
在Atari游戏中检验DQN算法时,网络结构、学习算法和超参数的设定都没有变,唯一变得是reward,并且将reward值修剪在-1——1之间。
在这个实验中,我们使用了RMSProp算法,最小的学习步数是32,策略是ε-greedy算法,在前一百万帧数据中,ε从1线性下降到0.1,之后保持固定不变。我们一共训练了大约5千万帧数据,记忆库的容量是一百万帧。 本实验借用了之前训练Atari算法时的技巧,使用了跳帧技巧,即不是每一帧都看、选择动作、学习,而是跳过几帧,在这跳过的几帧中选取的动作跟这几帧之前的动作相同。
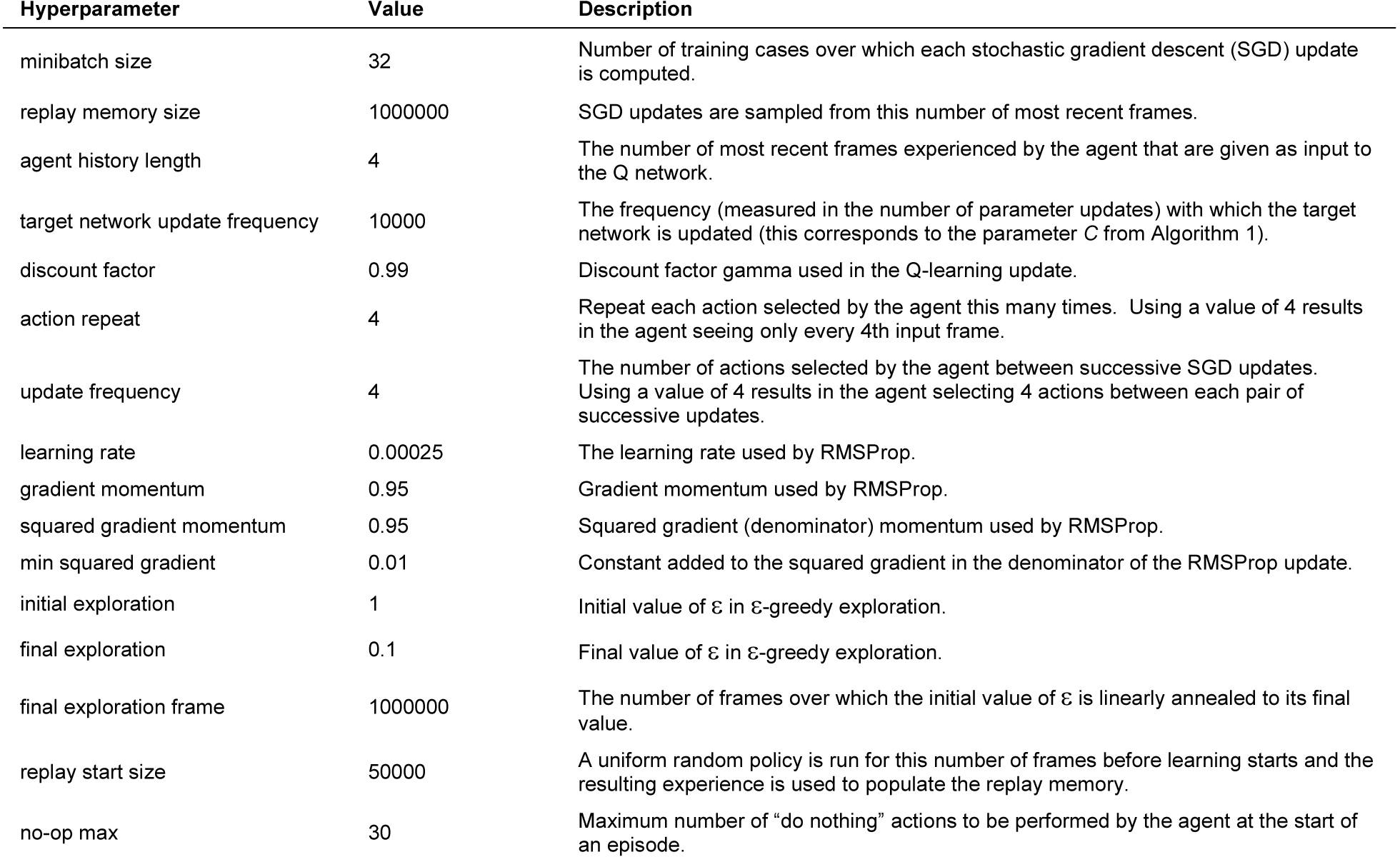
DQN算法中所采用的超参数的数值见extended data table1。
TensorFlow练完后:
Result of training for 24 hours using GTX 980 ti:
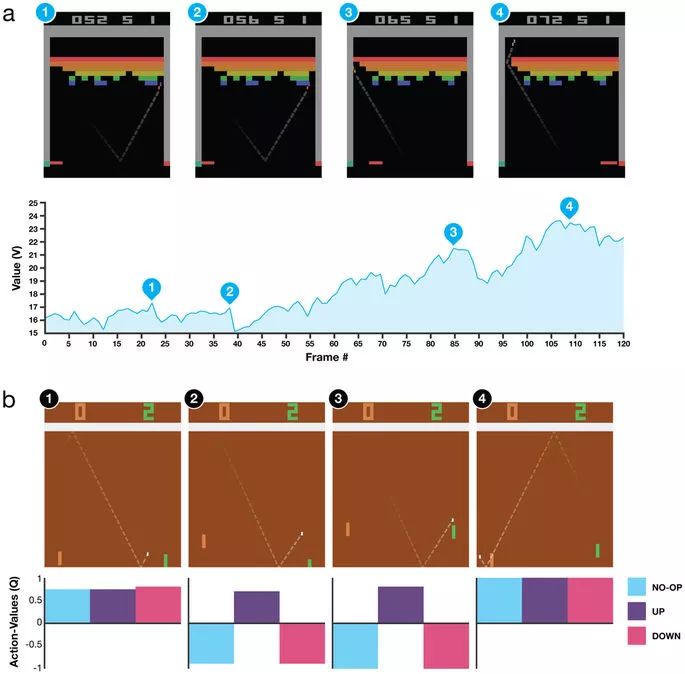
Extended Data Figure 2: Visualization of learned value functions on two games, Breakout and Pong.