【文章荐读】《星际穿越》之实值多变量维数约简

2018 年 3 月 5 日 中国自动化学会

想必看过《星际穿越》的小伙伴还对最后的五维空间记忆犹新。Cooper在飞船被黑洞吸力摧毁之前，弹出了飞船仓，自己在浩瀚的星际中掉进了黑洞。这时，他发现自己掉进了一个不存在时间概念的静止多维空间，在这个空间里，时间不再是线性的存在。Cooper在没有时间概念空间的状态中，连接到了自己家里书房，也就是女儿Murph小时候认为有鬼魂出现的地方。Cooper在那个神奇的时空里，看到Murph连接到所有的时间点。他通过推书架上的书，伸手，给Murph留下了信息。也就是说，Cooper自己告诉小Murph和他自己说不要走，要STAY。他给自己留了信息引导自己去找到了NASA接受任务。Cooper通过留给Murph的手表传递了信息给Murph，Murph此时也意识到这一切，其实父亲就是“鬼魂”，这实际是父亲留给自己的讯息，她破译了手表中暗含的摩斯码，成功的解决的重力方程问题。这样地球上的人类就有救了，Cooper此时意识到这一切都是自己使命，然后晕到在神奇的高维世界里。

电影中，Cooper从高维空间只能通过摩斯码来和另一个空间的Murph取得联系，而且Murph还大废周折，险些错过了Cooper的信息，可见高维空间沟通极其低效（如果真的错过了，那将是地球的灾难，所以高维空间会有“维数灾难”的问题）。如果能有一个方法可以帮助Cooper进入到一个低维空间，那么找到Murph岂不是会变得更容易，也无需在浩瀚的高维空间去寻找特有的时间点。那么这就是本文将要探讨的实值多变量维数约简。

实值多变量维数约简的定义如下：给定投影矩阵B的前提下，使得响应变量(集)Y与自变量X条件独立，表述如下式：Y⊥X|B^T X

这里符号“⊥”表示Y 独立于X. 其中X 和 Y均为多元的随机变量。投影矩阵B可以保证X投影后的子空间B^T X，获得的信息与原空间X相同，不会丢失任何信息。此时即使没有X，B^T X也可以完全用于对Y的预测，即条件独立性。

以《星际穿越》为例，这里的X就是Cooper所在的高维空间，Y为女儿Murph所在的低维空间（地球）。电影里面Cooper从高维空间给Murph发送摩斯码可以描述为：X→Y。电影里由于其传输的低效性，险些错过而导致地球灾难。

因为如果能通过找到一个合适的投影矩阵B，让Cooper沿着投影矩阵进入一个低维的空间，B^T X，（中心子空间），那么这个中心子空间或许就是Murph家的书房，亦或者是相交的某个空间，此时的Cooper只需要打个电话or打个飞的，就可以让Murph知道一切。这样问题也就变得简单多了。

作为机器学习的经典问题之一，维数约简主要用于处理维数灾难问题(指随着维度的增加，样本的数量需要指数级的增加)、帮助加速算法的计算效率和提高可解释性以及数据可视化. 传统的维数约简算法如主成分分析和线性判别分析等只能处理无标签数据或者分类数据. 然而，当预测变量为一元或多元连续型实值变量时，这些处理无标签数据或分类数据的维数约简方法则不能形成有效的预测性能. 近二十年来，有一系列工作从多个角度对这一问题展开了研究，并取得了系统性的研究成果. 在此背景下，本文将综述这些面向回归问题的降维算法，即实值多变量维数约简. 本文将介绍与实值多变量维数约简密切相关的基本概念、算法、理论，并探讨一些潜在的研究方向.

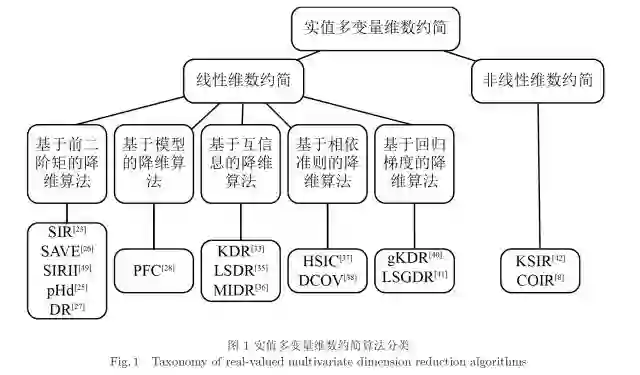
下图归纳了通过不同的技术手段实现实值多变量维数约简的大部分主流算法。