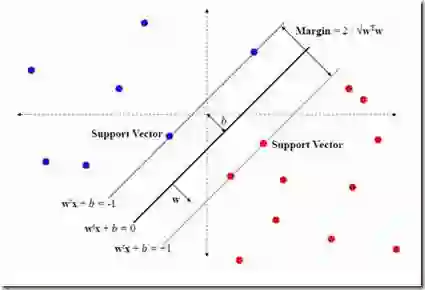
机器学习(18)之支持向量机原理(三)线性不可分支持向量机与核函数
微信公众号
关键字全网搜索最新排名
【机器学习算法】:排名第一
【机器学习】:排名第二
【Python】:排名第三
【算法】:排名第四
前言
在(机器学习(15)之支持向量机原理(一)线性支持向量机)和(机器学习(16)之支持向量机原理(二)软间隔最大化)中我们讲到了线性可分SVM的硬间隔最大化和软间隔最大化的算法,它们对线性可分的数据有很好的处理,但是对完全线性不可分的数据没有办法。本文我们就来探讨SVM如何处理线性不可分的数据,重点讲述核函数在SVM中处理线性不可分数据的作用。
多项式回归
在线性回归原理中,我们讲到了如何将多项式回归转化为线性回归。比如一个只有两个特征的p次方多项式回归的模型:
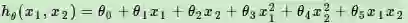
令
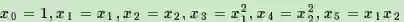
得到了下式:

可以发现,又重新回到了线性回归,这是一个五元线性回归,可以用线性回归的方法来完成算法。也就是说,对于二维的不是线性的数据,我们将其映射到了五维以后,就变成了线性的数据。这给了我们启发,也就是说对于在低维线性不可分的数据,在映射到了高维以后,就变成线性可分的了。这个思想我们同样可以运用到SVM的线性不可分数据上。也就是说,对于SVM线性不可分的低维特征数据,我们可以将其映射到高维,就能线性可分,此时就可以运用前两篇的线性可分SVM的算法思想了。
引入核函数
线性不可分的低维特征数据,可以将其映射到高维,就能线性可分。现在我们将它运用到我们的SVM的算法上。线性可分SVM的优化目标函数:
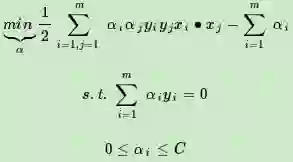
上式低维特征仅仅以内积xi∙xj的形式出现,如果我们定义一个低维特征空间到高维特征空间的映射ϕ(比如上一节2维到5维的映射),将所有特征映射到一个更高的维度,让数据线性可分,我们就可以继续按前两篇的方法来优化目标函数,求出分离超平面和分类决策函数了。也就是说现在的SVM的优化目标函数变成:
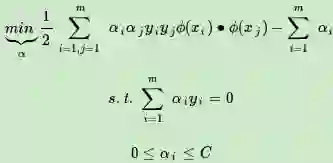
看起来似乎这样就已经完美解决了线性不可分SVM的问题了,但是事实是不是这样呢?我们看看,假如是一个2维特征的数据,我们可以将其映射到5维来做特征的内积,如果原始空间是三维,可以映射到到19维空间,似乎还可以处理。但是如果我们的低维特征是100个维度,1000个维度呢?那么我们要将其映射到超级高的维度来计算特征的内积。这时候映射成的高维维度是爆炸性增长的,这个计算量实在是太大了,而且如果遇到无穷维的情况,就根本无从计算了。
核函数的隆重出场
假设ϕ是一个从低维的输入空间χ(欧式空间的子集或者离散集合)到高维的希尔伯特空间的H映射。那么如果存在函数K(x,z),对于任意x,z∈χ,都有:

那么就称K(x,z)为核函数。
仔细观察上式可以发现,K(x,z)的计算是在低维特征空间来计算的,它避免了在刚才我们提到了在高维维度空间计算内积的恐怖计算量。也就是说,核函数的价值在于它虽然也是将特征进行从低维到高维的转换,但核函数好在它在低维上进行计算,而将实质上的分类效果(利用了内积)表现在了高维上,这样避免了直接在高维空间中的复杂计算,真正解决了SVM线性不可分的问题。
核函数详解
对于从低维到高维的映射,核函数不止一个。那么什么样的函数才可以当做核函数呢?由于一般我们说的核函数都是正定核函数,这里我们直说明正定核函数的充分必要条件。一个函数要想成为正定核函数,必须满足他里面任何点的集合形成的Gram矩阵是半正定的。也就是说,对于任意的,xi∈χ,i=1,2,3...m, K(xi,xj)对应的Gram矩阵K=[K(xi,xj)] 是半正定矩阵,则K(x,z)是正定核函数。从上面的定理看,它要求任意的集合都满足Gram矩阵半正定,所以自己去找一个核函数还是很难的,怎么办呢?下面我们来看看常见的核函数, 选择这几个核函数介绍是因为scikit-learn中默认可选的就是下面几个核函数。
线性核函数
线性核函数(Linear Kernel)其实就是我们前两篇的线性可分SVM,表达式为:
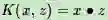
也就是说,线性可分SVM我们可以和线性不可分SVM归为一类,区别仅仅在于线性可分SVM用的是线性核函数。
多项式核函数
多项式核函数(Polynomial Kernel)是线性不可分SVM常用的核函数之一,表达式为:
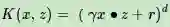
其中,γ,r,d都需要自己调参定义。
高斯核函数
高斯核函数(Gaussian Kernel),在SVM中也称为径向基核函数(Radial Basis Function,RBF),它是非线性分类SVM最主流的核函数。libsvm默认的核函数就是它。表达式为:
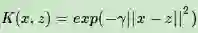
其中,γ大于0,需要自己调参定义。
Sigmoid核函数
Sigmoid核函数(Sigmoid Kernel)也是线性不可分SVM常用的核函数之一,表达式为:

其中,γ,r都需要自己调参定义。
SVM小结
引入了核函数后,我们的SVM算法才算是比较完整了。现在我们对分类SVM的算法过程做一个总结。不再区别是否线性可分。
输入是m个样本(x1,y1),(x2,y2),...,(xm,ym),,其中x为n维特征向量。y为二元输出,值为1,或者-1.
输出是分离超平面的参数和w∗和b∗和分类决策函数。
算法过程
1)选择适当的核函数K(x,z)和一个惩罚系数C>0, 构造约束优化问题
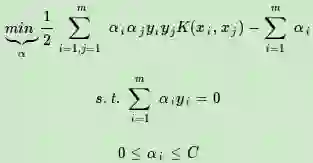
2)用SMO算法求出上式最小时对应的α向量的值α∗向量.
3) 得到
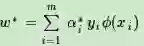
4) 找出所有的S个支持向量,即满足0<αs<C对应的样本(xs,ys),计算出每个支持向量(xs,ys)对应的偏置b,最终的偏置项为所有值的平均

最终的分类超平面为

最终的分类决策函数为
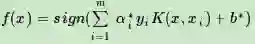
至此,我们的分类SVM算是总结完毕。
欢迎分享给他人让更多的人受益
参考:
博客园(作者:刘建平)
http://www.cnblogs.com/pinard/p/6103615.html
周志华《机器学习》
李航《统计学习方法》

加我微信:guodongwe1991,备注姓名-单位-研究方向(加入微信机器学习交流1群)
招募 志愿者
广告、商业合作
请加QQ:357062955@qq.com

喜欢,别忘关注~
帮助你在AI领域更好的发展,期待与你相遇!