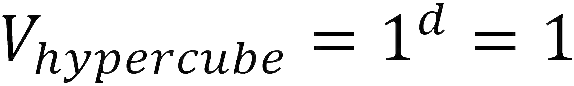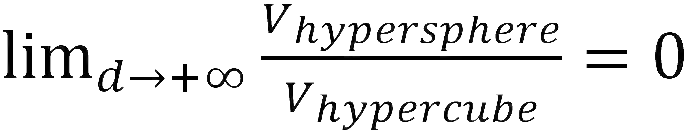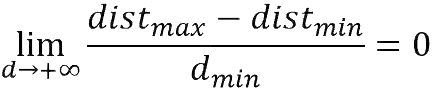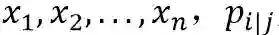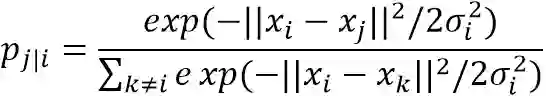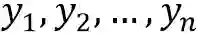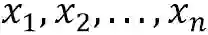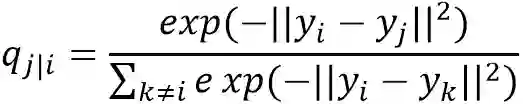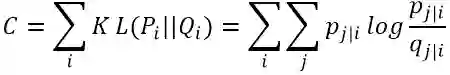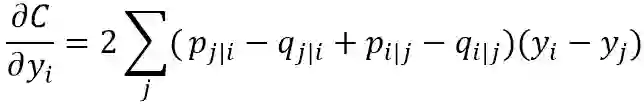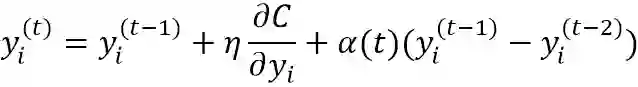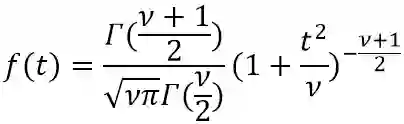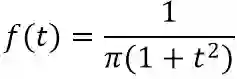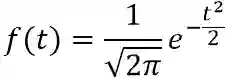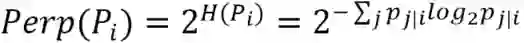t-SNE：最好的降维方法之一

引言

---

本期由来自哈工大的同样热爱科普的潮汐之子为我们带来t-SNE的全方位普及，作者的研究方向为自然语言处理。

说明

---

本文目的是做成一个60分钟t-SNE闪电入门简介，可能无法详细讲解原理，学术帝还请阅读原论文，或请移步我的另一篇博文，里面多了一些论文笔记，相关链接：

https://psubnwell.github.io/2017/12/01/paper-note-t-sne/

基础篇

认识高维空间：维数灾难

---

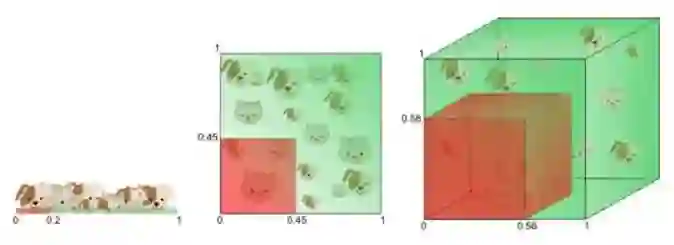
维数灾难（curse of dimensionality）：描述的是高维空间中若干迥异于低维空间、甚至反直觉的现象。该现象的详细论述可以阅读参考文献[1] ，其中通过超立方体和其内切球的推导十分精彩，这里不再赘述。

★高维空间中数据样本极其稀疏。需要维度几何级数的数据才能满足在高维空间密采样（dense sample）。反过来，高维数据降维到低维空间也将发生“拥挤问题（Crowding Problem）[2]”

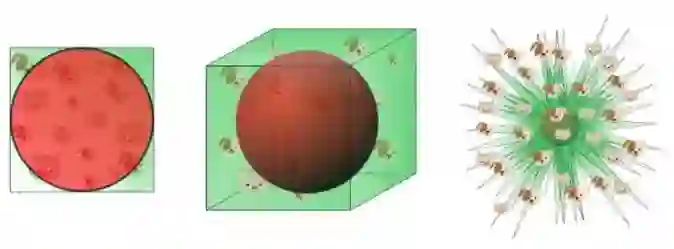
★高维单位空间中数据几乎全部位于超立方体的边缘。

几何学能给出高维空间中超几何体的体积，单位超立方体的体积为：

而其内切超球体的体积公式如下：

 对两者商做极限可得：

因此可以说一个高维单元空间只有边角，而没有中心。数据也只能处于边缘上，而远离中心。这样就直接导致了下一个性质：

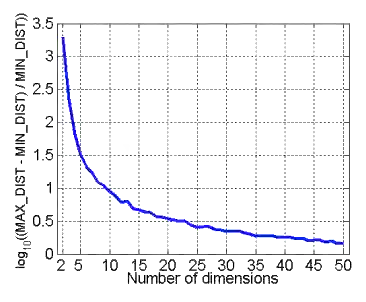
★欧氏距离失效（因此任何基于欧氏距离的算法也失效）。

上图描述的是高维空间中大距离和小距离的差异越来越不明显：

这是由上一性质自然推导出的结论。

降维

---

降维（dimension reduction）的基本作用：

★缓解维数灾难。即提高样本密度，以及使基于欧氏距离的算法重新生效。

★数据预处理。对数据去冗余、降低信噪比。

★方便可视化。

降维的概念中有两对直觉性的概念会反复出现：高维/低维空间、高维/低维数据。在文献中他们有若干别称[3]：

★高维空间（high-dimensional space），又叫原空间（original space）

★高维数据（low-dimensional data），也直接叫数据点（data points），用于和下述的映射点对应。

★低维空间（low-dimensional space），又叫嵌入空间（embedded space）、低维映射（low-dimensional map，map在此做名词用）等。

★低维数据（low-dimensional data），又叫低维嵌入（low-dimensional embeddings）、低维表示（low-dimensional representations）、映射点（map points）等。

嵌入（embedding）：数学上，嵌入是指一个数学结构经映射包含在另一个结构中。

★NLP目前所使用的词嵌入（word embedding）一词的本意可能就是这个意思。最初所使用的词向量是one-hot向量，维度等于词表大小（约几十万）。后来采用分布式表示的词向量，维度一般取几百维。因此我们认为分布式表示的词向量是更高维度语义空间的低维嵌入（embedding）。

★"Embed Everything！" 嵌入的思想不仅可以用在词（word）上，还能用于许多其他技术上。如知识图谱中可以把原先的网络结构也做嵌入，有实体嵌入、关系嵌入等。

降维技术可以分为线性和非线性两大类：

★线性降维技术。侧重让不相似的点在低维表示中分开。

①PCA（Principle Components Analysis，主成分分析）

②MDS（Multiple Dimensional Scaling，多维缩放）等

★非线性降维技术（广义上“非线性降维技术”≈“流形学习”，狭义上后者是前者子集）。这类技术假设高维数据实际上处于一个比所处空间维度低的非线性流形上，因此侧重让相似的近邻点在低维表示中靠近。

①Sammon mapping

②SNE（Stochastic Neighbor Embedding，随机近邻嵌入），t-SNE是基于SNE的。

③Isomap（Isometric Mapping，等度量映射）

④MVU（Maximum Variance Unfolding）

⑤LLE（Locally Linear Embedding，局部线性嵌入）等

流形学习

---

流形（manifold）：

★机器学习中指的流形指本征维度较低但嵌入在高维空间中的空间（a manifold haslow intrinsic dimensions, and is embedded within a space of much higher dimensionality[4] ）。比如上图中的S-curve数据集，本征维度=2（摊开来是一个二维空间），但被嵌在三维空间中。

★数学中提到流形，强调其具有局部欧式空间的性质，可以在局部应用欧几里得距离。但是在机器学习（流形学习）中，这个假设基本不成立。原因是高维空间由于维数灾难的存在，没有足够稠密的数据能在足够小的局部去近似该流形[5] 。

★但是流形概念中局部的思想仍可以借鉴。它为降维提供了另一个视角：从微观角度去探索高维数据结构。

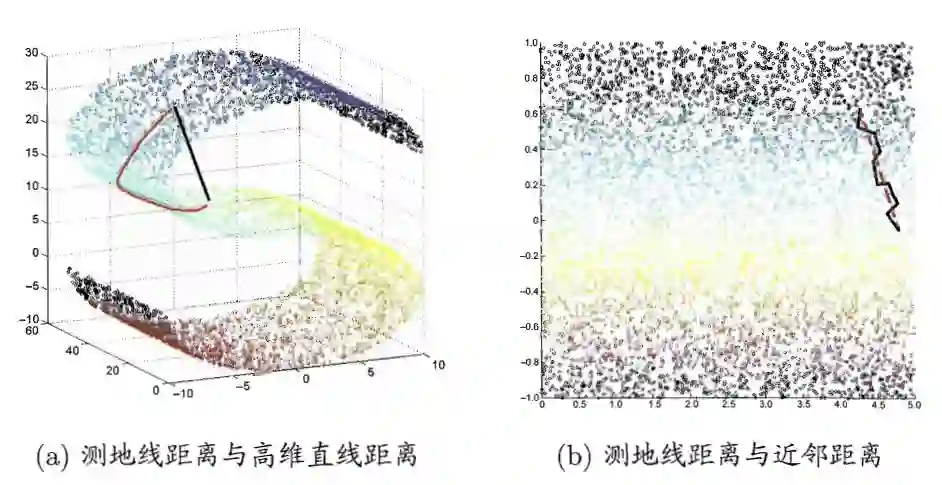
距离[6] ：想象你是一只蚂蚁，在图中的二维曲面流形上行走。

★高维直线距离：左图黑线。这个距离没有意义！

★测地线距离：左图红线，右图红虚线。这个距离才有意义！

★近邻距离：右图黑折线。用近邻距离可以拟合测地线距离。

学习：流形学习之所以叫学习，因为它不像PCA一类的纯线性代数降维方法，而是更像一个类似神经网络的学习算法。

★神经网络大部分是有监督学习；流形学习大部分是无监督学习。

★神经网络拟合一个分类函数；流形学习（以t-SNE为例）拟合高维数据的分布。

★神经网络学习参数；流形学习（以t-SNE为例）直接学习低维数据的表达。

★两者均有损失函数、梯度下降、迭代轮数等学习算法的特点。

学术篇

SNE

---

SNE（Stochastic Neighbor Embedding，随机近邻嵌入）[7] 

SNE两个主要思路/步骤：

★将欧氏距离转化为条件概率来表征点间相似度（pairwise similarity）。

★使用梯度下降算法来使低维分布学习/拟合高维分布。

给定高维空间的数据点：

是以x_i自己为中心，以高斯分布选择x_j作为近邻点的条件概率：

注意：

1）对除i外其他所有j都计算一个条件概率后，形成一个概率分布列，所以分母需要归一化；

2）默认p_(i|i)=0；

3）每不同数据点x_i有不同的σ_i，在此不展开。

同理，有低维空间的映射点：

分别对应：

q_(j|i)是y_i以自己为中心，以高斯分布选择y_j作为近邻点的条件概率：

注意：这里方差统一取σ_i=1/√2，若方差取其他值，对结果影响仅仅是缩放而已。

SNE的目标是让低维分布去拟合高维分布，则目标是令两个分布一致。两个分布的一致程度可以使用相对熵（Mutual entropy，也叫做KL散度，Kullback-Leibler divergences，KLD）来衡量，可以以此定义代价函数（cost function）：

其中P_i (k=j)=p_(j|i) 和Q_i (k=j)=q_(j|i)是两个分布列。

注意：KLD是不对称的！因为 KLD=plog(p/q)，p>q时为正，p<q时为负。则如果高维数据相邻而低维数据分开（即p大q小），则cost很大；相反，如果高维数据分开而低维数据相邻（即p小q大），则cost很小。所以SNE倾向于保留高维数据的局部结构。

对C进行梯度下降即可以学习到合适的y_i。

梯度公式：

带动量的梯度更新公式：（这里给出单个y_i点的梯度下降公式，显然需要对所有：Y^(T)={y_1,y_2,...,y_n}进行统一迭代。）

t-SNE

---

t-Distributed Stochastic Neighbor Embedding[8] 

事实上SNE并没有解决维度灾难带来的若干问题：

★拥挤问题（Crowding Problem）：在二维映射空间中，能容纳（高维空间中的）中等距离间隔点的空间，不会比能容纳（高维空间中的）相近点的空间大太多[9]。 

★换言之，哪怕高维空间中离得较远的点，在低维空间中留不出这么多空间来映射。于是到最后高维空间中的点，尤其是远距离和中等距离的点，在低维空间中统统被塞在了一起，这就叫做“拥挤问题（Crowding Problem）”。

★拥挤问题带来的一个直接后果，就是高维空间中分离的簇，在低维中被分的不明显（但是可以分成一个个区块）。比如用SNE去可视化MNIST数据集的结果如下：

如何解决？高维空间保持高斯分布不变，将低维空间的分布做调整，使得两边尾巴比高维空间的高斯分布更高，即可缓解拥挤问题。想一想为什么？（在下面t-分布中解释）

★UNI-SNE[10]：给低维空间的点给予一个均匀分布（uniform dist），使得对于高维空间中距离较远的点（p_ij较小），强制保证在低维空间中q_ij>p_ij （因为均匀分布的两边比高斯分布的两边高出太多了）。

t-分布（Student's t-distribution）

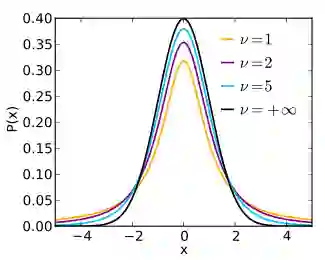
★t-分布的概率密度函数（probability density function，PDF）形式为：

其中 ν 是自由度。

figure of probability density function

★当 ν=1:

叫做柯西分布（Cauchy distribution），我们用到是这个简单形式。

★当 ν=∞:

叫做高斯/正态分布（Guassian/Normal distribution）。

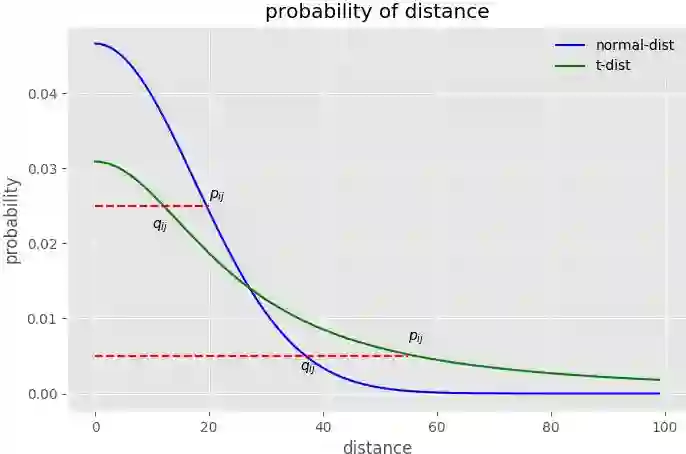
我们在低维空间的分布中，把原先用的高斯分布改成自由度为1的分布（把尾巴抬高）。下图可以很好地说明为什么“把尾巴抬高”可以很好地缓解拥挤问题。绘图代码参考 [11]

假设我们的低维数据分布对高维数据分布已经拟合完毕，则可以认为对于高维数据点x_i、x_j和低维映射点y_i、y_j，有p_ij=q_ij。我们用图中两条红线表示两种情况：

①上面的红线表示：当两个点相距相对近的时候，低维空间中比高维空间中相对更近。

②下面的红线表示：当两个点相距相对远的时候，低维空间中比高维空间中相对更远。

可以对比一下采用t-SNE对MNIST数据集的降维可视化效果:

以上是t-SNE的主要思想，其余还有若干知识点（如对称SNE、优化的技巧等），请参考论文[12]或者我的另一篇博文：论文笔记：Visualizing data using t-SNE，相关链接：

https://psubnwell.github.io/2017/12/01/paper-note-t-sne/

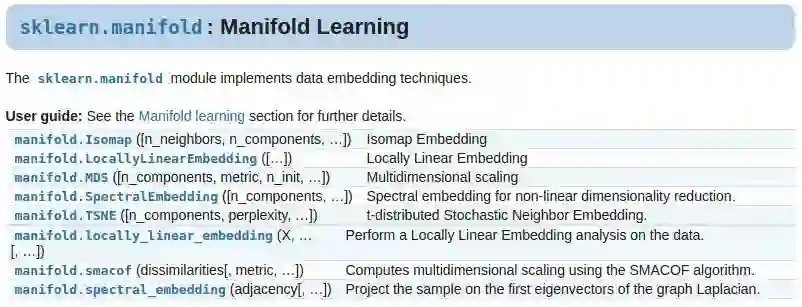
工程篇

Python库：sklearn.manifold

---

推荐阅读Python下著名的机器学习库scikit-learn的相应文档：sklearn.manifold.TSNE - scikit-learn，相关链接：

https://scikit-learn.org/stable/modules/manifold.html#t-distributed-stochastic-neighbor-embedding-t-sne

困惑度

---

使用t-SNE时，除了指定你想要降维的维度（参数n_components），另一个重要的参数是困惑度（Perplexity，参数perplexity）。

困惑度大致表示如何在局部或者全局位面上平衡关注点，再说的具体一点就是关于对每个点周围邻居数量猜测。困惑度对最终成图有着复杂的影响。

前面提到高维空间中每一个数据点x_i的高斯分布中的方差σ_i都必须设为不同。该方差σ_i须具有如下性质：在数据密集的地方要小，数据稀疏的地方要大。显然σ_i和困惑度有着相关关系。

如何给每个x_i分配σ_i值呢？

★可以手动分配[13] 

★使用算法分配：Binary search[14]或者 Root-finding method[15]

使用算法来确定σ_i则要求用户预设困惑度。然后算法找到合适的σ_i值让条件分布P_i的困惑度等于用户预定义的困惑度即可。

注意：困惑度设的大，则显然σ_i也大。两者是单调关系，因此可以使用二分查找。

论文[16]建议困惑度设为5-50比较好。这还是一个很大的范围，事实上在这个范围内，调节困惑度可以展示从微观到宏观的一系列视角，见下一节。

可视化

---

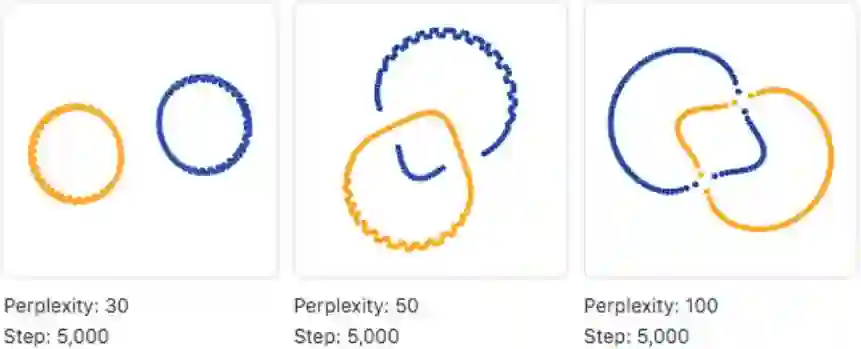
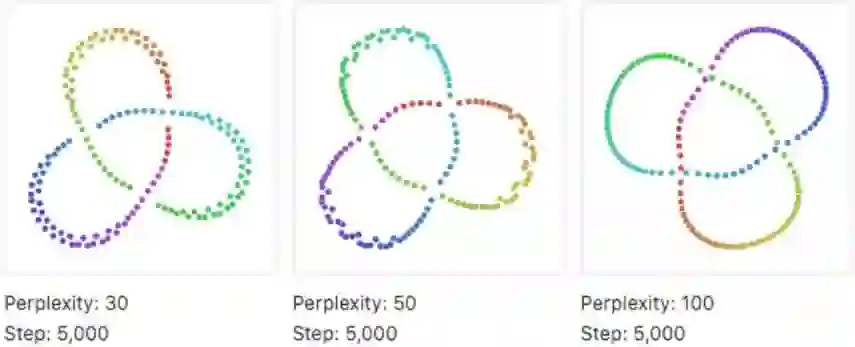
日常使用t-SNE可调的参数基本只有困惑度，非常简单。针对困惑度如何影响可视化结果，文献[17]做了非常详细的展示，还包含一个在线程序可以辅助认识。

文献[18]给出的基本结论如下：

★簇（cluster）的大小无关紧要。

★簇之间的距离无关紧要。

★密集的区域会被扩大，稀疏的区域会被缩小等。

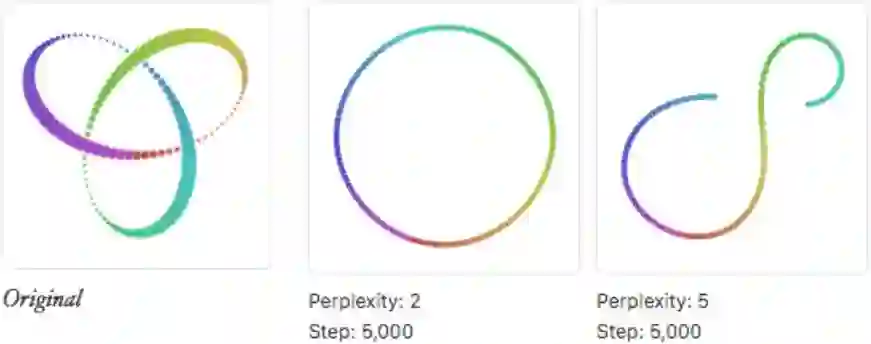
根据文献[19]给的图，说一点自己的理解：

★低困惑度对应的是局部视角，要把自己想象成一只蚂蚁，在数据所在的流形上一个点一个点地探索。

★高困惑度对应的是全局视角，要把自己想象成上帝。

t-SNE优点

---

流形学习中其他方法如Isomap、LLE等，主要用于展开单个连续的低维流形（比如“瑞士卷”数据集），而t-SNE主要用于数据的局部结构，并且会倾向于提取出局部的簇，这种能力对于可视化同时包含多个流形的高维数据（比如MNIST数据集）很有效。

t-SNE缺点

---

➊时间、空间复杂度为O(n^2)，计算代价昂贵。百万量级的数据需要几小时，对于PCA可能只需要几分钟。

➋升级版Barnes-Hut t-SNE可以让复杂度降为O(nlogn)，但只限于获得二维和三维的嵌入。（sklearn中可以直接使用参数method='barnes_hut'）

➌由于代价函数非凸，多次执行算法的结果是随机的（名字中“Stochatsic”的由来？），需要多次运行选取最好的结果。

➍全局结构不能很清楚的保留。这个问题可以通过先用PCA降维到一个合理的维度（如50）后再用t-SNE来缓解，前置的PCA步骤也可以起到去除噪声等功能。（sklearn中可以直接使用参数init='pca'）

尾声

---

作为一个三维生物，如何感知高维空间的形状，这个是历史难题。在读《三体》的时候，褐蚁的故事曾经让我若有所思，我将其摘录于此。它的方案和t-SNE是否有某种神似呢？

这次褐蚁来到故地，只是觅食途中偶然路过而已。它来到孤峰脚下，用触须摸了摸这顶天立地的存在，发现孤峰的表面坚硬光滑，但能爬上去，于是它向上爬去。没有什么且的，只是那小小的简陋神经网络中的一次随机扰动所致。这扰动随处可见，在地面的每一株小草和草叶上的每一粒露珠中，在天空中的每一片云和云后的每一颗星辰上……扰动都是无目的的，但巨量的无目的扰动汇集在一起，目的就出现了。...

与此同时，在前方的峭壁上，它遇到了一道长长的沟槽，与峭壁表面相比，沟槽的凹面粗糙一些，颜色也不同，呈灰白色，它沿着沟槽爬，粗糙的表面使攀登容易了许多。沟槽的两端都有短小的细槽。下端的细槽与主槽垂直，上端的细槽则与主槽成一个角度相交。当褐蚁重新踏上峭壁光滑的黑色表面后，它对槽的整体形状有了一个印象：“1”。...

很快，它遇到了另一道沟槽，它很留恋沟槽那粗糙的凹面，在上面爬行感觉很好，同时槽面的颜色也让它想起了蚁后周围的蚁卵。它不惜向下走回头路，沿着槽爬了一趟。这道槽的形状要复杂些，很弯曲，转了一个完整的圈后再向下延伸一段，让它想起在对气味信息的搜寻后终于找到了回家的路的过程，它在自己的神经网络中建立起了它的形状：“9”。...

褐蚁继续沿着与地面平行的方向爬，进入了第三道沟槽，它是一个近似于直角的转弯，是这样的：“7”。它不喜欢这形状，平时，这种不平滑的、突然的转向，往往意味着危险和战斗。...

孤峰上的褐蚁本来想转向向上攀登，但发现前面还有一道凹槽，同在“7”之前爬过的那个它喜欢的形状“9”一模一样，它就再横行过去，爬了一遍这个“9”。它觉得这个形状比“7”和“1”好，好在哪里当然说不清，这是美感的原始单细胞态；刚才爬过“9”时的那种模糊的愉悦感再次加强了，这是幸福的原始单细胞态。但这两种精神的单细胞没有进化的机会，现在同一亿年前一样，同一亿年后也一样。

参考文献

---

[1] The Curse of Dimensionality in classification（链接：http://www.visiondummy.com/2014/04/curse-dimensionality-affect-classification/）, 中文翻译：维度灾难（链接：https://zhuanlan.zhihu.com/p/27488363）

[2] Maaten, L. V. D., & Hinton, G. (2008). Visualizing data using t-SNE. Journal of Machine Learning Research, 9(Nov), 2579-2605.

[3] Maaten, L. V. D., & Hinton, G. (2008). Visualizing data using t-SNE. Journal of Machine Learning Research, 9(Nov), 2579-2605.

[4] Maaten, L. V. D., & Hinton, G. (2008). Visualizing data using t-SNE. Journal of Machine Learning Research, 9(Nov), 2579-2605.

[5] 有哪些关于流形学习（manifold learning）的好的资料或者课程？ - 知乎（链接：https://www.zhihu.com/question/41106133/answer/154709827）

[6] 周志华. 机器学习第十章[M]. Qing hua da xue chu ban she, 2016.

[7] Hinton, G. E., & Roweis, S. T. (2003). Stochastic neighbor embedding. In Advances in neural information processing systems (pp. 857-864).

[8] Maaten, L. V. D., & Hinton, G. (2008). Visualizing data using t-SNE. Journal of Machine Learning Research, 9(Nov), 2579-2605.

[9] Maaten, L. V. D., & Hinton, G. (2008). Visualizing data using t-SNE. Journal of Machine Learning Research, 9(Nov), 2579-2605.

[10] Cook, J., Sutskever, I., Mnih, A., & Hinton, G. (2007, March). Visualizing similarity data with a mixture of maps. In Artificial Intelligence and Statistics (pp. 67-74).

[11] t-SNE完整笔记。（链接：http://www.datakit.cn/blog/2017/02/05/t_sne_full.html）

[12] Maaten, L. V. D., & Hinton, G. (2008). Visualizing data using t-SNE. Journal of Machine Learning Research, 9(Nov), 2579-2605.

[13] Hinton, G. E., & Roweis, S. T. (2003). Stochastic neighbor embedding. In Advances in neural information processing systems (pp. 857-864).

[14] Hinton, G. E., & Roweis, S. T. (2003). Stochastic neighbor embedding. In Advances in neural information processing systems (pp. 857-864).

[15] Van Der Maaten, L. (2014). Accelerating t-SNE using tree-based algorithms. Journal of machine learning research, 15(1), 3221-3245.

[16] Maaten, L. V. D., & Hinton, G. (2008). Visualizing data using t-SNE. Journal of Machine Learning Research, 9(Nov), 2579-2605.

[17] Wattenberg, M., Viégas, F., & Johnson, I. (2016). How to Use t-SNE Effectively. Distill, 1(10), e2.（链接：https://distill.pub/2016/misread-tsne/）

[18] Wattenberg, M., Viégas, F., & Johnson, I. (2016). How to Use t-SNE Effectively. Distill, 1(10), e2.（链接：https://distill.pub/2016/misread-tsne/）

[19] Wattenberg, M., Viégas, F., & Johnson, I. (2016). How to Use t-SNE Effectively. Distill, 1(10), e2.（链接：https://distill.pub/2016/misread-tsne/）

@纯真学者出神入化

版权声明

本文版权归《纯真学者出神入化》，转载请自行联系。

点击下方阅读原文了解课程详情

历史文章推荐：

重磅 |《模式识别与机器学习》资源大礼包

从Word Embedding到Bert模型—自然语言处理中的预训练技术发展史

SFFAI分享 | 曹杰：Rotating is Believing

SFFAI分享 | 黄怀波 ：自省变分自编码器理论及其在图像生成上的应用

AI综述专栏 | 深度神经网络加速与压缩

SFFAI分享 | 田正坤 ：Seq2Seq模型在语音识别中的应用

SFFAI 分享 | 王克欣 : 详解记忆增强神经网络

SFFAI报告 | 常建龙 ：深度卷积网络中的卷积算子研究进展

SFFAI 分享 | 李宏扬 ：二阶信息在图像分类中的应用

点击下方阅读原文了解课程详情↓↓

---

若您觉得此篇推文不错，麻烦点点好看↓↓