【初学者系列】Factorization Machines 因子分解机详解

导读

Factorization Machines （FM）因子分解机是Steffen Rendle等人于2010年提出基于矩阵分解的机器学习算法，该模型结合了支持向量机（SVM）和因子分解模型的优点。本文详细介绍了FM的模型表示、推到过程以及使用FM实现一个简单的二分类任务。

FM为什么可以工作  

01

Factorization Machines （FM）是一种通用的预测器，可用于任何实值特征向量。与支持向量机一样，FM使用分解参数对变量之间的所有交互进行建模。因此，即使在支持向量机失效的推荐系统中，FM也能够估计出交互性。并且对于稀疏数据，FM可以很好地估计变量间的相互作用。

下面我们以论文中给的电影评分数据，通过实际的例子来解释为什么FM对于稀疏数据有很好的表现。数据集中每一条记录都包含了哪个用户u在什么时间t对哪部电影i打了多少分r。假定用户集U和电影集I分别为：

则数据集S为：

利用观测数据集S构造的特征向量与标签如下图所示：

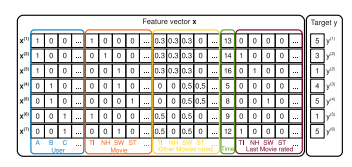
假设我们要估计爱丽丝（A）和《星际迷航》（ST）之间的相互作用，以预测A对ST的评级。显然，在训练数据中不存在变量x_A和x_ST都是非零的，因此直接估计将不会导致相互作用（w_{A，ST}=0）。但是，在这种情况下,FM可以通过因子化的相互作用参数<v_A,v_ST>，估计出A与ST之间的相互作用。

• 由于鲍勃对《星际迷航记》与《星球大战》两部电影都有相似的评分。故《星际迷航记》（ST）的因子向量很可能与《星球大战》(SW)中的因子向量相似。

• 这意味着爱丽丝（A）与《星际迷航》中的因子向量的点积（即相互作用）将与爱丽丝（A）与《星球大战》中的一个因子向量相似。

  
  

原理

02

与传统线性模型不用的是因子分解机（FM）考虑了两个互异的特征向量之间的相互关系，在传统线性模型的基础上加入了交叉项。度为2的模型方程定义为：

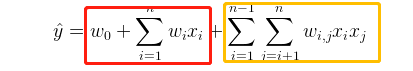
上图中，红色框部分就是传统的线性模型，黄色框部分为交叉项。

• w_0是全局偏置

• w_i为第i个变量的权重

• w_{i,j}是第i个和第j个变量之间的权重，模拟第i个变量与第j个变量间的相互关系

  
  

由于直接在交叉项 x_i,x_j 的前面加上交叉系数 w_{ij }的方式，在观察样本中未出现交互的特征分量时，不能对相应的参数进行估计，故文章作者引入了辅助向量V_i=（v_{i1},v_{i2}, ..., v_{ik}）利用<V_i,V_j>来对w{i,j}进行估计：

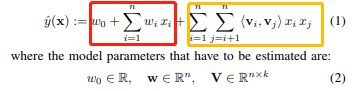
其中：

• <.,.>为两个大小为K的向量的点积：

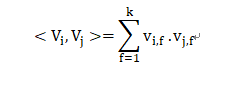
V中的行vi描述了具有k个因子的第i个变量。K是定义分解的维度的超参数，k 的大小称为 FM 算法模型的度。

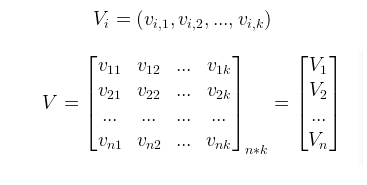
tips:k值的选取：若数据为稀疏的矩阵，k取较小值。

计算

03

接下来，将展示如何从计算的角度来应用FM。

在FM模型方程中，交叉项是最难计算的部分，对于交叉项的推倒，我们可以从矩阵的角度来理解。

1）首先根据[<V_1,V_1>x_ix_j,]定义一个n*n的矩阵

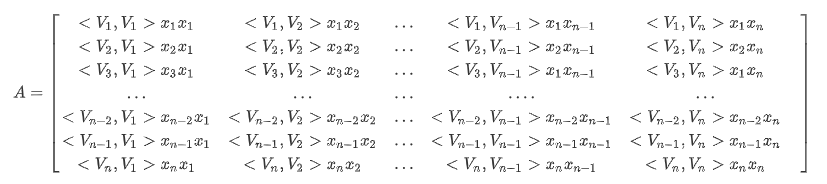
可以由矩阵A中观察到交叉项为矩阵A中除去对角线之后上三角元素的和：

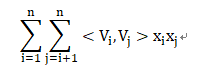
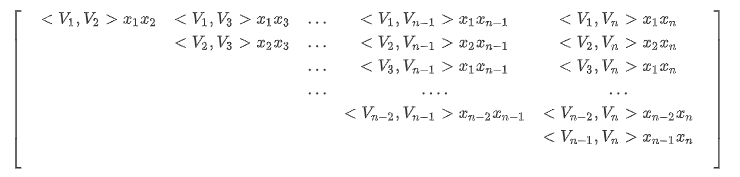
• 此矩阵中所有元素的和为：

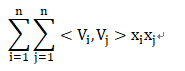
• 对角线元素之和为：

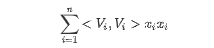
且矩阵中上、下三角元素之和相等，故：

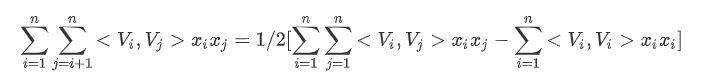
2）由于

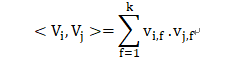
 故

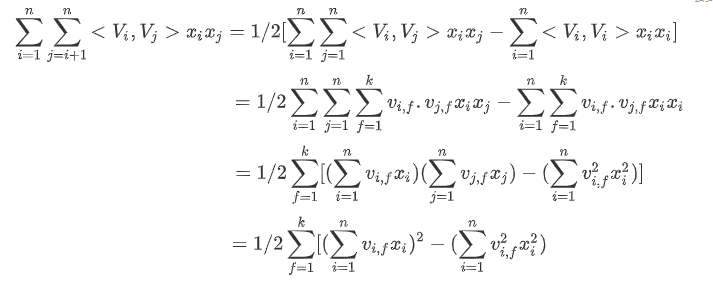
至此FM模型的目标函数可以表示为：

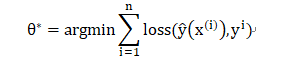
tips:通常添加L2正则项到优化目标中以防止过度拟合。

可以通过梯度下降方法（SGD）有效地学习FM的模型参数（w_0，w_i和V）

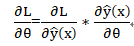
1）无论选择什么形式的损失函数，都可以先计算预测输出y的偏导：

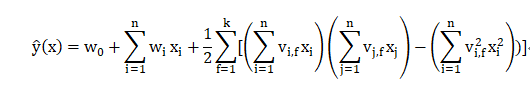
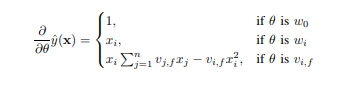
2）损失函数的选取：

• 回归问题：选择最小均方误差作为损失函数，即： 

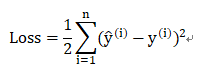
       求偏导得：

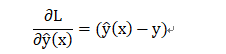
       即此损失函数下的梯度为：

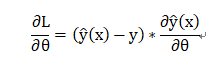
• 分类问题：选择对数损失函数，即：

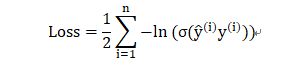
       其中：

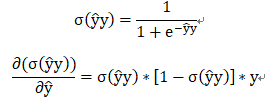
       即此损失函数下的梯度为：

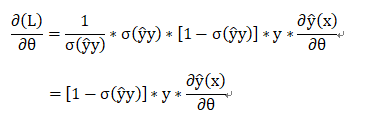
 实践

04

在了解了原理之后，让我们动手实践一下，利用FM实现一个简单的二分类！

• 加载数据

  训练数据与测试数据各两百个。

• 初始化参数

  将v按照正态分布进行随机初始化，w与w_0初始化为0。

• 计算

  在该部分主要计算损失函数以及准确率。

•  保存模型 

• 梯度下降法进行训练    
  

  开始训练，并将训练得到的w_0,w,v保存在weight_FM中。

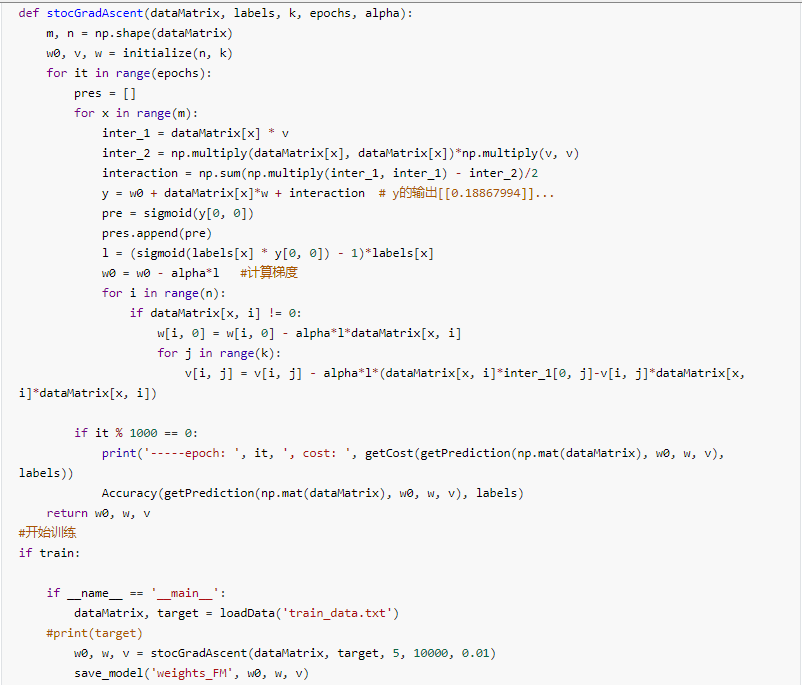
      训练结果如下：

      训练得到的权重

• 加载模型并保存预测结果    

• 测试

      部分测试结果如下：

至此，我们完成了用FM算法实现简单二分类的实践。

论文链接：https://www.csie.ntu.edu.tw/~b97053/paper/Rendle2010FM.pdf

参考链接：

https://github.com/GreenArrow2017/MachineLearning/tree/master/MachineLearning

https://github.com/Chaucergit/Code-and-Algorithm/tree/master/ML/3.Factorization%20Machine

获取代码

请关注专知公众号（点击上方蓝色专知关注）

后台回复“初学者系列FM”即可获取数据集以及全部代码。

-END-

专 · 知

专知，专业可信的人工智能知识分发，让认知协作更快更好！欢迎登录www.zhuanzhi.ai，注册登录专知，获取更多AI知识资料！

欢迎微信扫一扫加入专知人工智能知识星球群，获取最新AI专业干货知识教程视频资料和与专家交流咨询！

请加专知小助手微信（扫一扫如下二维码添加），加入专知人工智能主题群，咨询技术商务合作~

专知《深度学习:算法到实战》课程全部完成！560+位同学在学习，现在报名，限时优惠！网易云课堂人工智能畅销榜首位！

点击“阅读原文”，了解报名专知《深度学习:算法到实战》课程