古老的起源|计算进化史：改变数学的命运

会员服务 ·

古老的起源|计算进化史：改变数学的命运

2017 年 11 月 14 日 遇见数学 图灵新知

本文节选自《计算进化史》, 已获图灵许可. [遇见数学]特此感谢!

“

这部精巧之作展现了计算在数学中愈发重要的地位，宣告了算法数学时代的来临。这是一段关于“计算”与“数学”故事，散文般生动的文字让读者在阅读中领略数学思想的精粹。

- Bernard Chazell，普林斯顿大学

计算进化史：改变数学的命运

第 1 章从史前数学到希腊数学

数学史往往是从公元前 5 世纪的希腊开始讲起的。毕达哥拉斯创立了算术，泰勒斯和阿那克西曼德创立了几何，奠定了古代数学的两大分支。算术和几何的创立，无疑是数学史上的重大突破。然而，这样的讲法却忽略了一个重要的时代，也就是所谓的“史前”数学。人们并没有等到公元前5世纪才开始解决数学问题，特别是那些日常面临的具体数学问题。

会计师和土地测量师

“数学”活动最古老的痕迹之一是在美索不达米亚发现的一块泥板，它可以追溯到公元前 2500 年。这块泥板记录了这样一个计算：如果一个谷仓里有 1 152 000 份粮食，每个人分得7份，一共可以分给多少人呢？不出所料，结果是 164 571 人，即用 1 152 000 除以 7 得到的结果。看来，美索不达米亚的会计师在算术“诞生”之前很久就知道怎么做除法了。甚至，书写完全有可能就是为了记账才发明的——虽然这些事情很难说得准，但若真是如此，数字就比字母发明得还要早了。有些人也许不愿意接受这种推测，但我们所有的书写文化，很可能都要归功于不怎么浪漫的会计行当呢！

美索不达米亚和埃及的会计师不仅会做乘除法，而且掌握了许多其他的运算，比如解二次方程等。土地测量师则会计算矩形、三角形、圆形的面积。

“无穷”的闯入

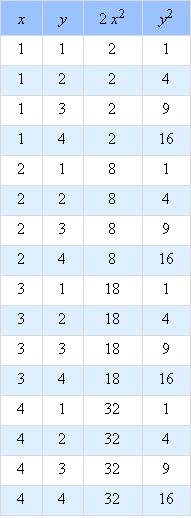
计师和土地测量师创造的技法构成了史前的算术和几何。那么，公元前5世纪的希腊到底发生了什么特别的事情，独独让这个时刻成为了数学史的开端呢？想要搞清楚这一点，让我先举个例子吧。毕达哥拉斯有个学生，姓名已然不可考了，但他解决了这样一个问题：比如以米为单位，要找出一个等腰直角三角形，让三条边的长度都是自然数。因为三角形是等腰的，两条短边的长度一样，我们就设这个长度为 x，然后设长边，也就是斜边的长度为 y。因为这又是一个直角三角形，根据毕达哥拉斯定理(勾股定理)， $y^{2}$ 就等于 $x^{2} + x^{2}$ 。这个问题最终归结为：找出两个自然数 x 和 y，使得 $2 \times x^{2} = y^{2}$ 。让我们来试试 4 以内所有 x 和 y 的可能性吧（见表 1.1）。

向上滑动阅览表 1.1:

4 以内 x 与 y 的所有可能性

在所有这些情况里， $2 \times x^{2} \neq y^{2}$ 。我们还可以在更大的数字范围里继续寻找，事实上，毕达哥拉斯学派很可能寻找了很久，却没能找到解。后来，他们终于相信这个解不存在。他们是怎么说服自己这个解不存在的呢？显然不是试遍了所有的数对，因为这样的数对有无穷多个。你就算试到 1000 甚至 100 万，证实没有数对能满足条件，可你还是没法保证在更大的数字里面不可能有解……

让我们来重新构建一个思路吧，也许毕达哥拉斯学派就是由此得出这个结论的。

首先，在找解的时候，我们只要在 x 和 y 至少有一个是奇数的情况里找就行了。因为比方说 x=202，y=214 是一组解，那么把两个数都除以 2 就可以得到另一组解 x=101，y=107。所以，至少要有一个数是奇数。再推广一点，我们任取一组解，把两个数反复除以 2，总归会得到一组至少有一个数是奇数的解。如果这个问题有解，就必然存在 x 和 y 中至少有一个是奇数的解。

第二个想法是把数对分成 4 类：

两个数都是奇数；
第一个数是偶数，第二个数是奇数；
第一个数是奇数，第二个数是偶数；
两个数都是偶数。

有了这两个想法，我们就可以分 4 种情况证明，但这 4 种情况中没有一个能够构成 x 和 y 至少有一个是奇数的解，所以这个问题就没有至少有一个数是奇数的解，也就是说，这个问题根本没有解。

我们先从第一类开始：x 和 y 至少有一个是奇数的解不存在。因为如果 y 是奇数，则 $y^{2}$ 也是奇数。它不可能等于 $2 \times x^{2} = y^{2}$ ，因为后者必然是偶数。这一论证也同样适用于第二类，即 x 是偶数而 y 是奇数。第四类本身就不成立，因为根据定义，数对中的两个数不可能都是偶数。现在只剩下第三类，即 x 是奇数而 y 是偶数。但在这种情况下， $2 \times x^{2} = y^{2}$ 的一半是奇数，而 $y^{2}$ 的一半却是偶数 -- 这两个数不可能相等。

一个平方数不可能是另外一个平方数的两倍 -- 这个由毕达哥拉斯学派在 2500 多年前得到的结果，迄今在数学上仍占有重要地位。它证明了，如果你画一个短边长度为 1 米的等腰直角三角形，那么以米为单位的话，斜边的长度是 $\sqrt{2}$ 。这个数稍大于 1.414，却无法通过两个自然数 y 和 x 相除得到。由此，几何揭示了一些不能通过自然数的四则运算，即加、减、乘、除得到的数。

几个世纪之后，这个发现启发数学家们构造出了新的数——实数。但毕达哥拉斯学派没有走到这一步，他们还没有准备好放弃自然数这个基本观念。对他们而言，这个发现更像一场灾难，而不是前进的动力。

这个问题的革命性不仅仅在于它对未来数学的巨大影响，还在于它本身的性质及其解决的方法。首先，与美索不达米亚泥板上铭刻的把 1 152 000 份粮食除以 7 份的问题相比，毕达哥拉斯学派的问题更为抽象：美索不达米亚的会计师关注的是粮食的份数，而毕达哥拉斯学派的问题仅涉及数字本身。同样，这个问题的几何形式并没有谈到三角形的田地，而就是三角形这个形状。从三角形的田地到三角形，从粮食的份数到数字，迈向抽象这一步的意义不可小觑。田地的面积无非有几平方千米。如果这个问题说的是三角形的田地而不是抽象的三角形，我们挨个尝试 x 和 y 小于 10 000 的所有数字，或许就能解决问题了。然而，抽象的三角形和田地不同，它的面积可以轻易大到上百万甚至上亿平方千米。

公元前5世纪的重大革命，就是抽象的数学对象与自然中的实际物体之间的分离，即使数学对象本身就是从实际物体中抽象出来的也不例外。

数学对象与自然物体之间的分离，让一些人认为数学不适合描述自然物体。这种看法一直活跃到伽利略的时代（公元 17 世纪），直至数学物理的成就将其打消。然而直到今天，一些人的脑海里还残留着数学与人文科学毫无关系的观点。用玛丽娜·雅盖洛的话来说，数学在语言学中的作用就是“将语言学作为‘人文科学’故而本质上就不精确的那一面掩藏在数学公式里”。

自这场革命之后，数学研究的对象不再是必须与实际物体相关的几何图形和数字。研究对象性质的变化，最终引发了解决数学问题的方法的革命。让我们再来比较一下美索不达米亚泥板上的问题和毕达哥拉斯学派的问题各自的解决方法吧：第一个问题是通过计算解决的——做一个简单的除法就行了，而要解决第二个问题，就需要进行推理了。

要做除法，我们在小学里学过的算法就够用了，美索不达米亚人也会做类似的计算。然而，要进行毕达哥拉斯学派的推理，没有任何算法会教你把数对分成四组。毕达哥拉斯学派应该是发挥了想象力才得到了这个思路。也许有一个门徒明白了数字 y 不能是奇数；过了几个星期或者几个月，另一个门徒又取得了一些进展，发现 x 也不能是奇数；然后，几个月甚至几年都卡在这里，直到又有一个门徒有了新想法。美索不达米亚人在做除法时，他知道自己会得到什么样的结果，甚至事先预知这个除法要算多久。反过来，当毕达哥拉斯学派的门徒面对算术问题时，他不可能知道要花多少时间才能找到一种能够解决问题的推理，甚至不确信是不是有找到答案的那一天。

学生们有时会抱怨数学太难学——数学需要想象力，而且没有系统化的方法来解决所有问题。这种说法确有其道理。数学对于专业数学家来说就更难，有些问题要花几十年甚至几百年才能解决。面对数学问题束手无策并不稀奇，数学家们也会在难题面前“卡壳”，有时甚至要到很久之后才能找到答案。但是，如果做个除法也要“卡壳”好几个钟头，这就说不过去了——因为只要应用一个人所共知的算法就行了。

研究对象性质的变化是如何引发解决问题的方法发生变化的呢？换句话说，古希腊数学是如何完成从计算到推理的标志性转变的呢？毕达哥拉斯学派的问题为什么就不能用计算解决呢？我们再来和美索不达米亚泥板上的问题比较一次吧。泥板上的问题针对的是一个特定的物品，即装满了粮食的谷仓，谷仓的体积是已知的。而在毕达哥拉斯学派的问题中，三角形是未知的——这正是我们需要去求解的对象。这个问题说的不是某个特定的三角形，而是会涉及所有可能的三角形。而且，由于三角形的尺寸没有限制，问题会同时涉及无穷多个三角形。因此，在数学对象的性质发生变化的同时，“无穷”闯入了数学——方法的改变势在必行，要用推理来代替计算。我们在前面已经提到，如果这个问题仅涉及有限个三角形，比如所有边长小于 10 000 米的三角形，那还是可以依靠计算来尝试所有不超过 10 000 的数对。当然，手动计算起来无疑十分麻烦，但问题还是可以有条不紊地得到解决。

在公元前5世纪的希腊发生的这场从计算到推理的转变，被视为数学的诞生。

最初的推理规则：哲学家与数学家

那么，到底什么是推理呢？如果我们知道所有的松鼠都属于啮齿目，所有的啮齿目动物都是哺乳动物，所有的哺乳动物都是脊椎动物，所有的脊椎动物都是动物，我们就可以推导出一个结论：所有的松鼠都是动物。推理让我们得到了这个结论，这背后是一套连续的推导：所有的松鼠都是哺乳动物，因此所有松鼠都是脊椎动物，因此所有的松鼠都是动物。

这个推理简单得不能再简单了，但它的结构和数学推理在本质上并无二致。无论哪种推理，都是由一系列命题构成的，每个命题都是用先前的命题通过逻辑得出的，也就是按照“演绎推理规则”构造的。在此情况下，我们把同一个规则连用了三次：如果我们已经知道所有的 Y 都是 X，所有的 Z 都是 Y，就可以推导出所有的 Z 都是 X 。

古希腊的哲学家为我们总结了最初的演绎规则，它可以让推理进行下去，也就是从已证的命题演绎出新的命题。例如，上述这条规则要归功于亚里士多德，他提出了一套叫作“三段论”的规则。三段论的另一种形式是“有些……是……”：如果知道所有的 Y都是X，有些 Z 是 Y，我们就可以演绎出有些 Z 是 X 。

亚里士多德并不是唯一一位对演绎规则感兴趣的古代哲学家。公元前 3 世纪的斯多葛学派提出了另一套规则。例如，如果有命题“如果 A，那么 B ”和命题 A，则有一条规则可以演绎出命题 B。

这两派总结演绎规则的尝试，正值从计算转向推理的方法论革命之后，古希腊算术和几何的蓬勃发展时期。因此我们可以想见，古希腊的数学家会使用亚里士多德或者斯多葛的逻辑来进行推理。比如，在证明一个平方数不可能是另一个平方数的两倍时，就可以用到三段论。奇怪的是，事实并非如此，尽管古希腊哲学家和数学家很显然是志同道合的。比如，在公元前 3 世纪，欧几里得写了一篇专著，综合了他那个时代的几何知识。他的专著结构完全是演绎式的，其中提到的每一件事都给出了推理证明，但欧几里得却从来没有用到过亚里士多德或斯多葛的逻辑。

有几种假设可以来解释这件事。最可能的一种假设是说，数学家没有使用亚里士多德或斯多葛的逻辑，是因为它们太粗糙了。在斯多葛的逻辑中，可以用来推理的是“如果 A，那么 B”形式的命题，其中 A 和 B 是所谓的“原子命题”，表述了一个简单事实，比如“苏格拉底必死”或者“天亮了”。于是，斯多葛逻辑的命题就是用“如果……那么……”“和”“或”等连词联系起来的一些原子命题。这是一种非常贫乏的语言设计，里面只有两种语法类别——原子命题和连词。它并没有考虑到原子命题，比如“苏格拉底必死”可以拆分成主词“苏格拉底”和谓词（或属性）“必死”。

亚里士多德的逻辑和斯多葛不同，它承认了“谓词”的概念。推理中出现的 X、Y、Z 表达就恰恰是谓词——松鼠、啮齿目、哺乳动物……然而，亚里士多德的逻辑中并没有“专有名词”，即指代个人或物体的名词，比如“苏格拉底”。这是因为，对于亚里士多德来说，科学并不关心苏格拉底这样的特定个人，而是仅仅关心广义的概念，比如“人”“必死”……所以，人们常常用来举例的三段论——“所有人都是必死的，苏格拉底是人，所以苏格拉底是必死的”——并不会出现在亚里士多德的逻辑中。对他来说，三段论应该是：“所有人都是必死的，所有哲学家都是人，所以所有哲学家都是必死的。”所以说，在亚里士多德的逻辑中，命题并不是由主词和谓词构成的，而是由两个谓词和一个泛指代词“所有”或“某些”构成的。直到中世纪末，亚里士多德的逻辑才得到拓展，加入了专有名词“苏格拉底”等单称项。然而，即使有了这样的拓展，亚里士多德的逻辑对于表达某些数学表述来说还是太粗糙了。有了单称项“4”和谓词“偶数”，我们当然可以构造命题“4 是偶数”，但它却没有办法构造命题“4 比 5 小”，因为“偶数”只作用于单个对象，而谓词“比……小”与之不同，它要作用于两个对象，即“4”和“5”，并让两者形成一个关系。同理，它也没有办法构造命题“直线 l 穿过了点 A”。

我们现在明白了，为什么古希腊的数学家没有使用同时代哲学家提出的逻辑来进行新生的算术和几何推理——因为这些逻辑不够丰富，做不到。在非常长一段时期内，如何构造一套丰富的、足以支撑数学推理的逻辑这一问题似乎并没有引起多少人的兴趣。除了个别人的几次尝试之外，比如 17 世纪莱布尼茨所做的研究，直到 19 世纪末的 1879 年，戈特洛布·弗雷格才重新拾起了这个问题，并提出了一套逻辑。但是，一直等到阿尔弗雷德·诺思·怀特海与伯特兰·罗素在 20 世纪初提出类型论，并且大卫·希尔伯特在 20 世纪 20 年代提出了谓词逻辑之后，这些工作才取得了具体的成果。

不过，我们还是先继续看看古希腊的数学吧。虽然没有显式的演绎规则来构造数学推理，但这并没有让数学止步不前。直到 19 世纪，数学命题的语法和演绎规则只不过不那么明确而已。这种情况在科学史上屡见不鲜——在缺乏工具的时候，人们就会想方设法对付一下，而这些变通又常常为工具的出现奠定了基础。

不过对于几何而言，欧几里得明确提出了“公理”的概念：这是无需证明的事实，也是构造证明的基础。特别是著名的平行公理，用现代的形式表述是这样的：过给定直线外一点，有且仅有一条直线与之平行。

长期以来，欧几里得的专著《几何原本》一直都被视为数学方法的原型：先提出公理，然后利用显式或隐式的演绎规则，由公理证明定理。从这个角度来看，推理才是解决数学问题的唯一途径，这也反映出古希腊数学家和哲学家对于推理的重视。

古希腊数学家利用公理化方法发现了一种新的数学。也许，他们还曾试图理解这种新的数学是如何从美索不达米亚人和古埃及人更古老数学的发展而来的。如果古希腊人真的这样做了，他们就应该会去思考如何将计算和推理融合起来。然而这并不是他们的目的——相反，他们将过去一抹而净，完全抛弃了计算，而代之以推理。

正因如此，在古希腊之后，计算在数学大厦之中就难有立锥之地了。

第 2 章　计算两千年

公理化方法确立之后，人们常常把推理视为解决数学问题的唯一工具。数学家们在自己学科的论述中，几乎不给计算留什么空间。然而，计算却并没有从数学工作中消失——无论在哪个时代，数学家都提出了一些新算法来系统地解决某些类型的问题。数学史有它光彩照人的一面——猜想、定理和证明，也有躲在幕后的一面——计算。

在这一章里，我们将看到数学史中三个重要的时刻。这三个重要时刻分属于不同的时代，启发我们讨论不同的问题。

首先，我们将反思如何解决数学论证与数学实践的明显矛盾——前者几乎没有给计算立足之地，而后者却非常依赖计算。这一矛盾还让我们思考从史前数学到希腊数学的转变是如何发生的。接下来，我们会讨论中世纪数学如何传承了美索不达米亚和古希腊的数学遗产。最后，我们要想一想，为什么古代的几何都是围绕着少数几种几何形状，如三角形、圆、抛物线……而大量的新几何形状——悬链线、旋轮线等都是直到 17 世纪才出现。

欧几里得算法：基于推理的计算

虽然欧几里得的名字与几何和公理化方法紧紧地联系在了一起，但颇为讽刺的是，他的名字也出现在一个用于计算两个自然数的最大公约数的算法——欧几里得算法(辗转相除法)中。

最初的一种计算两个数的最大公约数的方法，就是挨个用比它们小的数来试除，然后找到那些“正好除尽”的数字，从而确定每个数的约数。比如，要计算 90 和 21 的最大公约数，我们可以先求出 90 的约数（1、2、3、5、6、9、10、15、18、30、45 和 90）和 21 的约数（1、3、7和21），然后只要找到两个列表中同时出现的最大数字，即 3。想要回答诸如“90 和 21 的最大公约数是不是等于 3？”或者“90 和 21 的最大公约数是多少？”的问题，我们根本用不着推理，只需应用上述这个虽然烦琐却条理清晰的算法就行了，它基本上就是把最大公约数的定义简单阐释了一遍。

欧几里得算法可以让我们用不那么烦琐的方式计算两个数的公约数。它的思路是这样的：要计算两个数 a 和 b（比如 90 和 21）的最大公约数，我们可以用较小的数 b 去除较大的数 a。如果“正好除尽”，得到的商是 q，那么 a = b x q。这时，b 就是 a 的约数，也是 a 和 b 公约数，并且它是最大的，因为对 b 来说，没有比 b 本身更大的约数了。所以 b 就是 a 和 b 的最大公约数。反过来，如果除法“没有除尽”，留下了余数 r，那么 a = b x q + r。在这种情况下，a 和 b 的公约数也是 b 和 r的公约数。所以，我们可以用 b 和 r 来代替 a 和 b，它们的最大公约数是一样的。欧几里得算法会反复进行这个计算，直到得到两个做除法时能够“正好除尽”的数，而我们要找的最大公约数就是这两个数中比较小的那一个。如果用欧几里得算法计算 90 和 21 的最大公约数的话，我们会把数对 (90, 21) 换成 (21, 6)，再换成 (6, 3)。由于 6 是 3 的倍数，3 就是我们要的结果。

对于 90 和 21 这两个数来说，欧几里得算法会在进行 3 次除法之后得到结果。更一般来说，无论开始的数字是什么，都可以在有限次计算后得到结果。事实上，在把 a 换成 r 的时候，计算最大公约数的数对越来越小，而递减的自然数数列必然是有限的。

这个例子说明，欧几里得等古希腊人并没有把计算弃置一旁，反而创造出了新的算法。这也展示了推理和计算如何在数学实践中融合起来。和第一个计算最大公约数的算法不同，欧几里得算法的构造要求我们证明几个定理：首先，如果 a 能被 b 除尽，那么 a 和 b 的最大公约数就是 b；其次，如果 r 是 a 除以 b 的余数，那么 a 和 b 的公约数也是 b 和 r 的公约数；再次，除法的余数总是比除数小；最后，递减的自然数数列是有限的。这些结果都建立在推理之上，就像毕达哥拉斯学派证明一个平方数不可能是另一个平方数的两倍一样。

第一个算法的设计不需要推理，但这是个特殊情况。一般来说，仅仅把定义解释一遍是不够的，想要设计出欧几里得算法这样的计算方法需要推理才能完成。

泰勒斯的定理：数学的发明

算法的设计可能需要推理。回过头来看，这个事实就给美索不达米亚和古埃及的数学带来一个问题：就拿美索不达米亚人来说吧，他们是怎么不靠推理就琢磨出了除法的算法的呢？或许，美索不达米亚人和古埃及人可能有某种暗含的推理方式。和希腊人不同，他们并没有明确地采取推理活动，比方说把推理过程写在泥板上。他们多半并没有意识到推理对于解决抽象数学问题的重要性，但这却并没有影响他们进行推理，就像莫里哀笔下的茹尔丹先生一样，说话如同散文一般却不自知[2]。

[2] 茹尔丹先生是莫里哀剧作《贵人迷》的主人公，他努力想提高修养，跻身贵族，却闹出许多笑话。——译者注

人们常常强调在设计算法时进行推理的必要性。正因如此，美索不达米亚人和古埃及人虽然没有明确的推理记载，人们却仍然猜测他们进行了推理。然而很少有人指出，正是在这种必要性的启发下，古希腊数学产生了奇迹——从计算到推理的转变。确实，我们可以假设，正是在为设计新算法而进行推理时，古希腊人认识到了推理的重要性。

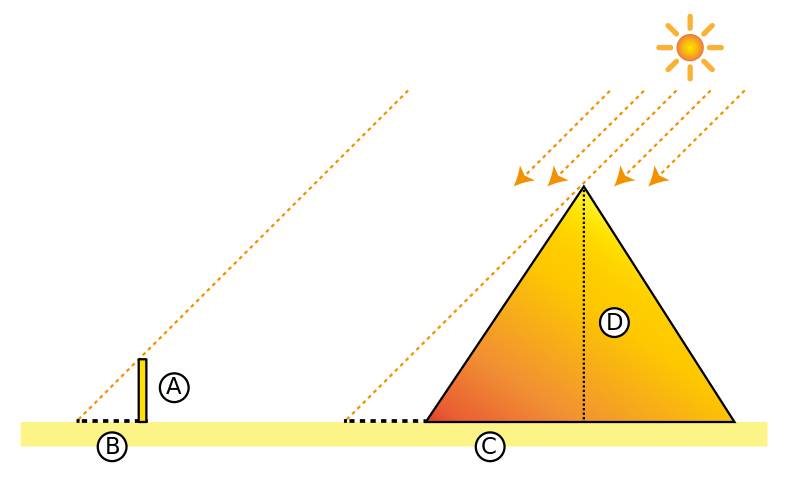
例如，我们常把“第一个”几何推理归功于泰勒斯。金字塔太高，高度无法直接测量。为了测量它的高度，泰勒斯想到了一个办法：他测量了金字塔在地上的投影长度，再单独测量了一根小木棒的高度和影长，然后应用比例法则。

Thales Theorem 演示, 图自网络

看起来，泰勒斯的目标是设计一个新算法来计算线段的长度。在构造算法时，他需要证明金字塔和它的投影的比例与木棒及其投影的比例相同。这个定理由此拥有了它内在的价值，也就是我们今天所说的“平行线分线段成比例定理”[3]。

[3]本定理亦称“截线定理”。在法语中称为“泰勒斯定理”(Théorème de Thalès)，但汉语和英语中的“泰勒斯定理”常指另一条定理，即直径所对圆周角为直角。——译者注

论证与实践

欧几里得算法的存在还提出了另一个问题，就是数学论证与数学实践的明显矛盾——前者几乎没有给计算立足之地，而后者则非常依赖计算。古希腊人和后来者是怎么一边声称只有推理重要，一边又构造了这些算法的呢？

我们再来看看这个算法是怎么计算 90 和 21 的最大公约数的。一种说法是，我们就是按照算法的说明，“盲目地”把数对 (90,21) 换成了 (21,6)，又换成了 (6,3)，最后得到了 3，这时发现它确实求出了这两个数的最大公约数。换一种说法，我们要说明把数对 (90,21) 换成 (21,6) 是有道理的，证明 90 和 21 的最大公约数等于 21 和 6 的最大公约数。这只需要用到前面说到的一个定理就行了：数 a 与数 b 的最大公约数和 b 与 r 的最大公约数相等，其中 r 是 a 除以 b 的余数。如果用后面这种表述方法，我们就可以完全不提欧几里得算法的事，而只是利用了前面的两个定理，就证明了 90 和 21 的最大公约数是 3。

更具体来说，除了得到结果等于 3 之外，欧几里得算法还构造了一套推理，可以证明 90 和 21 的最大公约数是 3。一旦这个推理完成之后，它是怎么来的就不重要了——只要存在就行了。假如古希腊人及后来者确实认为计算只是构造推理的工具，而且构造“工具”应该隐藏在构造“成果”的背后，那么古希腊数学的矛盾——在数学实践中使用计算，却在数学论证中几乎绝口不提计算——似乎也是情有可原的。

进位制

现在来看看数学史上的第二个时刻吧。我们平常总觉得，如何表示数学对象以及日常生活中的物体，只是个细枝末节的问题。把狮子叫作“狮子”或者把老虎叫作“老虎”并没有什么特别的道理。我们也完全可以另选两个词，只要保证使用完全相同的用法，换个名字也还是一回事。语言学家把这种现象称为符号的“任意性”。同样，我们也完全可以给数字“三”换个词，或者给“3”换个书写符号，也不会有什么大的不同。其他语言本来就用别的词表示数字，比如德语中的“drei”或英语中的“three”，德国人和英国人的数学和我们的数学仍然是一样的。

要是让符号的“任意性”更进一步，我们可能会觉得把数字三十一写成“三十一”“IIIIIIIIIIIIIIIIIIIIIIIIIIIIIII”“XXXI”“3X 1I”还是“31”都没什么区别。然而并不完全是这么回事。

首先，为什么我们觉得需要一种特殊的语言来写数字呢？在科学和其他领域，我们要给用到的对象起名字，但一般来说，这并不需要发明一种特殊的语言。比如，人们给每个化学元素都发明了一个名字：氢、氦……但这还是中文啊。然而化学元素虽多，毕竟是有限的。同样的道理，人们也给每个小的数字都起了一个特殊的名字：“一”“二”“三”……以及一个特殊的符号：“1”“2”“3”……然而数字和化学元素不同，它可是无穷无尽的：给每个数字都起个名字是不可能的，因为一门语言中的符号和单词是有限的。

由此诞生了一种思想：把有限的不同符号组合成无限个符号，用来表示数字。也就是说，不是创造一组词汇，而是发明一套语法——这就是一门语言了。虽然词汇是任意的，但语法的随意性就小得多了，而且对于推理和计算而言，数字语言的某些语法就比别的语法更为实用。在“三十一”“IIIIIIIIIIIIIIIIIIIIIIIIIIIIIII”“XXXI”“3X 1I”和“31”中间，最后一个表示法是最好的：数字“3”表示的是十的个数，而这是通过位置体现出来的。这样，如果把一个数字写在另一个数字下方，个位就对齐个位，十位对齐十位……这样做加减法就会很方便。尤其是做乘法的算法变得简单了——要把数字乘以 10，只要在后面加个 0，也就是把数字向左移一格就可以了。

这种进位制来自于美索不达米亚，其雏形在公元前 2000 年就开始使用了。不过，美索不达米亚人用的体系太复杂，后来印度数学家把它简化了。随后在 9 世纪时，印度体系通过一本叫作《代数学》的书传到了阿拉伯世界。该书的作者是阿尔–花拉子米（al-Khwārizmī），这就是“算法”（algorithm）一词的由来。中世纪的数学家花了几个世纪来完善进位制带来的算法。这套体系在12世纪传到了欧洲。

花拉子米雕像

中世纪的欧洲数学家由此继承了双重的遗产：一面是来自希腊，而另一面又通过进位制吸取了美索不达米亚的数学思想，而后者至少与前者同等重要。

公理化方法的发现并没有扼杀计算。相反，通过继承美索不达米亚的数学遗产，计算的问题一直存在，并成为了中世纪数学家眼中的重要课题。

微积分

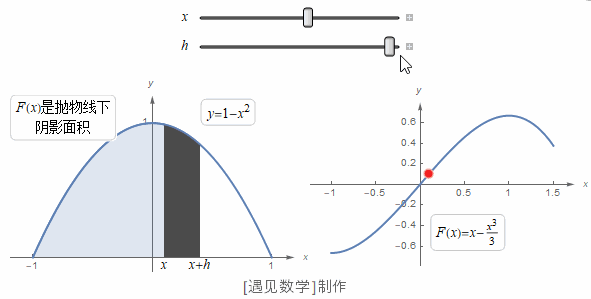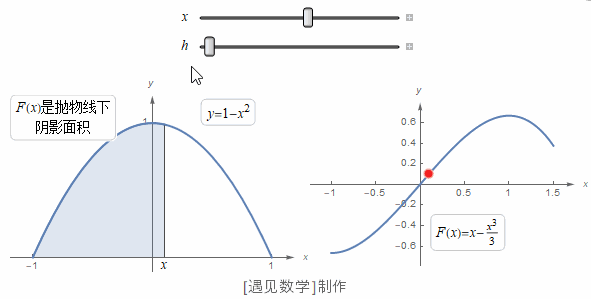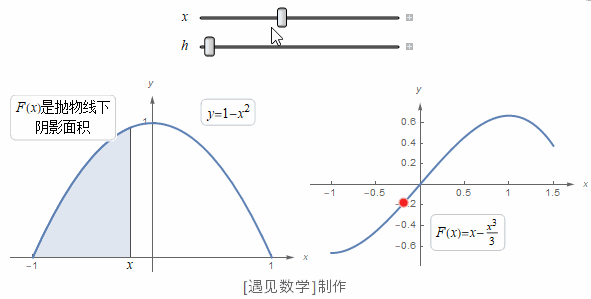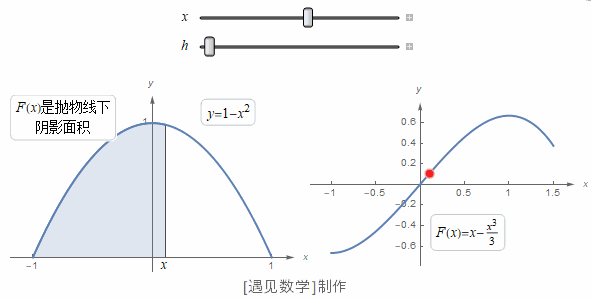
在看过了欧几里得算法和四则运算之后，我们现在来看看数学史上的第三个时刻：微积分。微积分是 17 世纪由卡瓦列里、牛顿、莱布尼茨等人共同建立起来的。然而它的根源却可以追溯到古代阿基米德的两个发现：一个是圆的面积，另一个是抛物线弓形的面积。

如今，大家都知道圆的面积等于半径的平方再乘以 3.1415926...。阿基米德还没有得出这一步，但他已经证明圆的面积落在半径的平方的 3+10/71=3.140... 倍和 3+10/70=3.142... 倍之间。换句话说，他已经得出了数字 π 的两位小数。对于抛物线弓形的面积，阿基米德则得出了一个精确解：抛物线弓形的面积等于内接三角形面积的 4/3 倍。

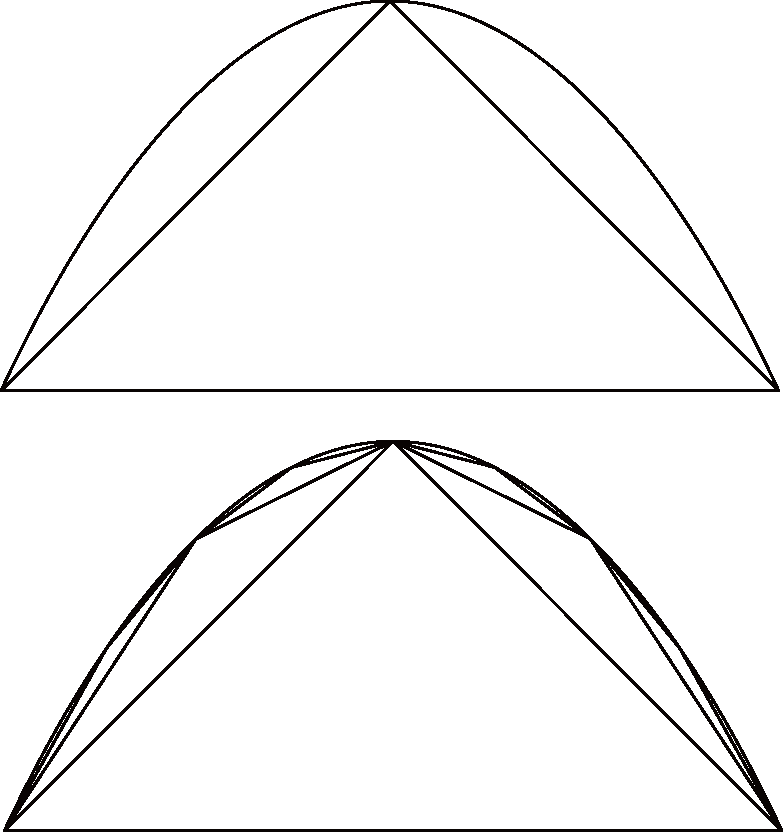
为了得到这一结果，阿基米德把抛物线弓形分成了无数个小三角形，然后把它们的面积加起来。

设抛物线内接三角形的面积为单位一，那么根据定义，第一个三角形的面积自然是1。我们可以证明它两侧的两个三角形的总面积是 $\frac{1}{4}$ ，再外侧的四个小三角形的总面积是 $\frac{1}{16}$ ⋯每组三角形的面积都是前一组三角形的 $\frac{1}{4}$ 。于是抛物线弓形的面积就是所有这些三角形的面积总和： $1+ \frac{1}{4} +(\frac{1}{4})^{2} +(\frac{1}{4})^{3} + \dots$ ，这个无穷数列的和是有限的： $\frac{4}{3}$ 。阿基米德可能对给无穷多个数求和还心存疑虑，他就考虑了有限和1、 $1+ \frac{1}{4}$ 、 $1+ \frac{1}{4} +(\frac{1}{4})^{2}$ ⋯ 也就是抛物线内接多边形的面积，它总是比抛物线弓形本身的面积小。他证明了抛物线弓形的面积不可能小于 $\frac{4}{3}$ ，否则就会小于某个内接多边形了，而这是不可能的。阿基米德还利用外接多边形进行了另一套论证，证明了抛物线弓形的面积不会超过 $\frac{4}{3}$ 。如果面积既不能大于 $\frac{4}{3}$ 也不能小于 $\frac{4}{3}$ ，那它就只能等于 $\frac{4}{3}$ 了。

到了 16 世纪，佛兰德斯数学家西蒙.斯蒂文和法国数学家弗朗索瓦.韦达等数学家开始计算无穷数列求和，那么在推理上就不用兜这么大圈子了。然而，阿基米德的推理就算简化了一点，要证明每组三角形的面积都是前一组面积的 $\frac{1}{4}$ 也是要大费周章的。所以，直到 17 世纪，计算几何图形的面积都是件让人伤脑筋的事。

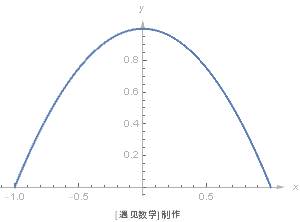
到了 17 世纪，在勒内·笛卡儿发明了坐标表示法之后，人们就顺理成章地用方程来表示曲线了。比如，前面图中的抛物线就可以用方程来表示。

有了方程，我们就可以想想如何计算抛物线弓形的面积，即曲线与横轴之间部分，而不用把它分解成一堆三角形了。17 世纪数学家们的一大发现，恰恰就是计算曲线围绕的图形面积的方法——只要曲线可以用方程来表示，并且这个方程足够简单。

第一步，找出曲线围成的面积与另一个概念——导数之间的联系。

让我们来考虑一个函数，比如说变量为 x，值为 $x- \frac{x^{3}}{3}$ 的函数。这个函数在 x+h 处的值是 $(x+h)- \frac{(x + h)^{3}}{3}$ 。简单的代数推理就可以证明，该函数在 x+h 处与在 x 处的值之差是 $h- x^{2} h-x h^{2} - \frac{h^{3}}{3}$ 。于是这个函数在 x 和 x+h 之间部分的"增长率"就是这个差值除以 h，结果是 $1- x^{2} -xh- \frac{h^{2}}{3}$ 。

这个函数在点 x 上的瞬时增长率，也就是在 x 处的"导数"，就是上面这个增长率在 h 趋于 0 时的结果：最后两项消失了，只留下了 $1- x^{2}$ 。

不过，如果只是为了求函数 $x- \frac{x^{3}}{3}$ 的导数，就用不到上面这些推理过程了。实际上，我们可以证明两个函数之和的导数就是其导数之和。我们只需要求出 x 的导数，再求出 $- \frac{x^{3}}{3}$ 的导数，然后加起来就好了。接下来，我们还可以证明函数乘上一个常数之后，其导数也要乘上这个值，所以只需要知道 $x^{3}$ 的导数再乘上 $- \frac{1}{3}$ 。最后，为了求出 x 和 $x^{3}$ 的导数，只需要知道 $x^{n}$ 的导数是 ${nx}^{n - 1}$ 。那么 $x- \frac{x^{3}}{3}$ 的导数就是 $1 - x^{2}$ 。

求 $x- \frac{x^{3}}{3}$ 的这两种方法有什么区别呢？对于第一种方法，我们需要进行一个小小的推理，虽然很简单，但也需要动动脑筋。而第二种方法只需应用规则，就可以按部就班地求出导数了：

●和的导数等于导数之和；

●常数倍的导数等于导数的常数倍；

$x^{n}$ 的导数是 $n x^{n - 1}$ 。

一旦证明了这三条规则的正确性，求函数的导数就是一个简单的计算了。这个求导数的方法不是用于数字，而是用于函数表达式。而且，并不是所有的函数表达式都适用，而只适用于能够通过 x 和常数的加法和乘法得出的函数 -- 多项式。更为普适的算法可以处理更丰富的数学语言，比如指数函数、对数函数和三角函数等，不过本质上并没有什么不同。

x 的函数 $1 - x^{2}$ 是函数 $x- \frac{x^{3}}{3}$ 的导数。反过来，我们说函数 $x- \frac{x^{3}}{3}$ 是 $1 - x^{2}$ 的一个"原函数"。我们可以证明这个函数有好多个原函数，都是在这个原函数上加一个常数得到的。

再回过头来看看求导的规则，构造出一套求原函数的规则也不难：

● 和的原函数等于原函数之和；

● 常数倍的原函数等于原函数的常数倍；

$x^{n}$ 的原函数是 $x^{n + 1} /(n+1)$ 。

一步步应用这个算法，我们就可以求出 $1 - x^{2}$ 的一个原函数： $x - \frac{x^{3}}{3}$ 。

让我们回到求面积的问题上。微积分的基本定理把面积和原函数的概念联系了起来。如果设 F(x) 是横坐标为 x 的竖线左侧的抛物线部分的面积，由于函数 $1 - x^{2}$ 是连续的，不难证明函数 F 的导数就恰好是 $1 - x^{2}$ 。

换句话说，函数 F 是 $1 - x^{2}$ 的一个原函数：它是 $x - \frac{x^{3}}{3}$ 加上一个常数。由于在 x=-1 时 F 的值是 0，这个常数值就只能是 $\frac{2}{3}$ ，那么 F 就是 $x- \frac{x^{3}}{3} + \frac{2}{3}$ 。抛物线形的面积就是这个函数在 1 处的值，即 $\frac{4}{3}$ 。我们得到了和阿基米德一样的结果，不过用的方法却不是把抛物线弓形拆成小三角。如果想求曲线 $y=1- x^{2}$ 围成的抛物线弓形的面积，就用不着构造一套复杂的推理来求拆分出来的这些小三角的面积了 -- 只要用前面说的方法求出 $1 - x^{2}$ 的原函数，然后调整常数，满足 -1 处的值是 0，再取 1 处的值就可以了。

与求导算法一样，这个算法也只能用于多项式。更普适的算法确实可以处理更复杂的数学语言，不过推广起来不像求导算法那么方便。在三个多世纪的时间里，求原函数的过程一直混杂着算法与技巧，并需要一定的熟练度，一会儿偏计算，一会儿偏推理。直到 20 世纪开发了形式计算程序，积分算法理论才形成体系。我们后面还会讲到它。

回到 17 世纪，随着导数和原函数概念的出现，以及相应算法的建立，许多求面积，甚至求体积、长度、重心...的问题都被简化为简单的计算。一类问题的解法系统化了，求解起来容易了，人们就可以探索更广阔的数学世界。古代的数学家已经求出了某些图形的面积，而 17 世纪的数学家走得要远得多。要求出某些复杂曲线，比如 $y=2- x^{2} - x^{8}$ 在 -1 和 1 之间围成的面积，古代数学家会头疼不已，然而对于 17 世纪的数学家来说就是小菜一碟：只要计算 $2- x^{2} - x^{8}$ 的一个在 -1 处等于 0 的原函数 $(2x- \frac{x^{3}}{3} - \frac{x^{9}}{9} + \frac{14}{9})$ ，再取原函数在 1 处的值，就得到了结果： $\frac{28}{9}$ 。这些算法工具让我们能够对付那些在"赤手空拳"时看似难比登天的问题。没有这些工具时无法研究的一些新几何图形也在 17 世纪出现了。