看精彩美剧学数学 - 数字追凶103：向量

我们每天都在使用数学，预报天气、查看时间，还有……数钱。数学绝不仅仅只是方程和公式，它是逻辑的，是有理的，它使人们通过思考来解决所面临的各式谜题

103 Vector

涉及数学内容：

零号病人(patient zero), 病毒载体(viral vector), 向量分析, SIR传染病模型

洛杉矶地区突然开始流行了一种怪病，很多人得病会感到恶心、发烧然，然后迅速恶化直至呼吸衰竭死去。

Don怀疑这是生化主义恐怖分子，与携手公众卫生局展开调查，邀请Charlie进行矢量分析来追踪患者之间的联系，希望可以预测疾病的传播。

追踪病毒传播过程属于统计分析与图论问题，其计算非常复杂。想象零号病人(第一个感染者)与4名健康人同处一室，然后2人被感染。之后5人又分别走入到其他的房间，这样更多的人会被感染将病毒继续扩散，到了100间房间的时候，就非常难找到最初的零号病人了。

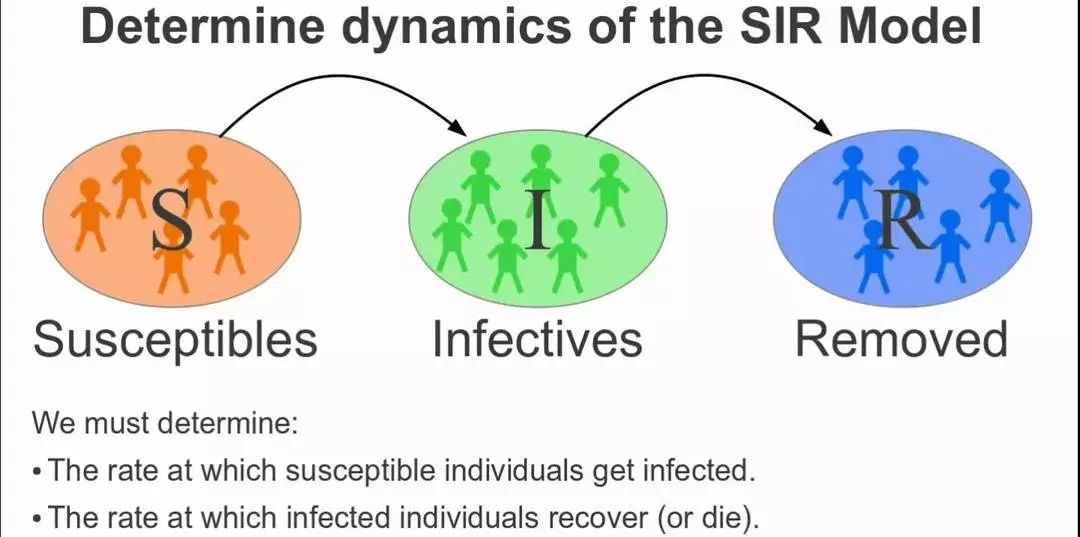
经过和患者的亲友询问，FBI们得到了一些有用的信息，Charlie从建立的SIR模型中(SIR模型是传染病模型中最经典的模型，其中S表示易感者，I表示感染者，R表示移出者)成功的发现了规律——这些病都是从联合火车站散播出去的，而整个病毒的扩散就像南北生长开来的两棵树。

在更加深入调查后，他们终于知道了疾病的种类，病原体是西班牙流感，能够导致大范围传染的流感 。这种流感曾经在1918爆发过，是全球流行病，极其恶性，死亡率甚高，且无药可治，在当年导致美国6个月内60万人染病死去。

接着，FBI查出了四个正在研究西班牙流感的生物实验室，其中有一个实验室Gen-O就在洛杉矶本地，监督研究的博士是Weaver。他介绍到在50年前科学家就从阿纳斯加的永久冻结带中一名病死的士兵肺中找到了西班牙流感病菌的完整DNA，他们实验室已经复原了这种流感病毒。

医药公司需要这些病毒以便来研发针对西班牙流感的专用疫苗，否则一旦病毒再次进入到人类社会还会导致一场全球性的流行病。

Charlie随后又和卫生局产生了分歧，因为卫生局认为联合火车站就是散播点，在这里释放病毒符合逻辑，但经过检查在那里并没有发现病毒的踪迹。大学同事Lorry提醒他，想要得到答案还必须回到数据本身。

经过思考Charlie认为真正的散播点是商业区主要公共汽车总站，开往南北两个方向的两辆公交车上是最初病毒散播地方，并且调整过的模型更符合实际情况，准确度提高了36%。

而数据表明，北边的死亡率远远高于南边，受感染死去的人有80%来自北方，令Don不解，为什么同样的病毒在两边会有不同的效果呢？Charlie提出来可能不是相同的病毒。

卫生局经过对比后确认了Charlie的推论，原来南北方向是同宗病毒两个不同的变种，尽管结构存在细微差异，但作用到人身上致死率却大相径庭。Charlie经过对两种病毒的量化差异分析，帮助卫生局找到一种治疗方案，成功将一部分染病者从死亡边缘挽救回来。

经过更进一步分析往北方向扩展的就是Gen-O实验室所复原的病毒，该病毒更加恶性的，这就造成了更多人染病死去，而另一个Russell实验室所复原病毒则不显得那么“完美”。

最后，在查看了汽车总站的录像之后，散播病毒的人竟然是一直协助调查并且看起来温和的DR.Weaver...

Weaver为了证明自己实验室所复原的病毒更强大，以此来提醒CDC(美国疾病控制与预防中心)对疫苗和治疗方法不要选用来自Russell实验室错误的病原体，自己亲自散播了两种病毒，但也导致了20位无辜的人因此去世。（本集终）

最后以SIR Model结束第一季第3集吧，希望大家多多支持【遇见】！未来会有相关内容介绍此模型。