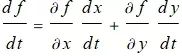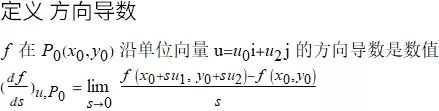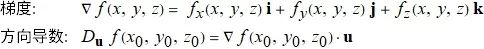11.5 方向导数, 梯度向量和切平面
根据链式求导法则可知, 如果 f(x,y) 是可微的,则 f 沿曲线 x=g(t), y=h(t) 对于 t 的变化率是下面式子:
![]()
上面式子 f 对于 t增量的变化率依赖于沿曲线运动的方向.
![]()
方向导数的解释
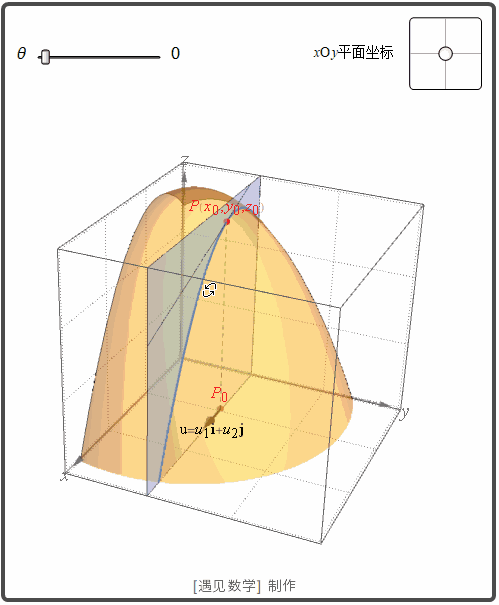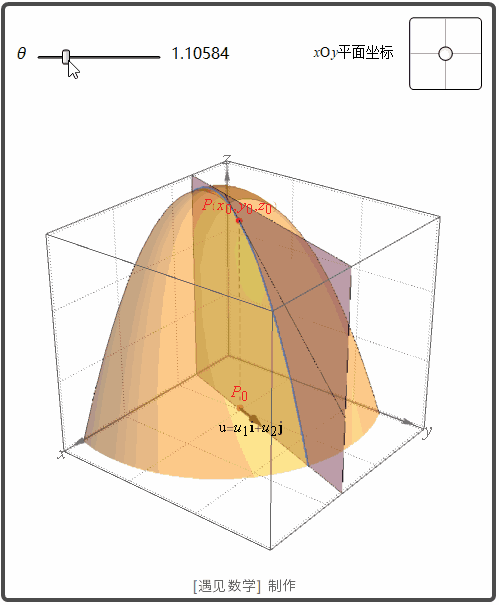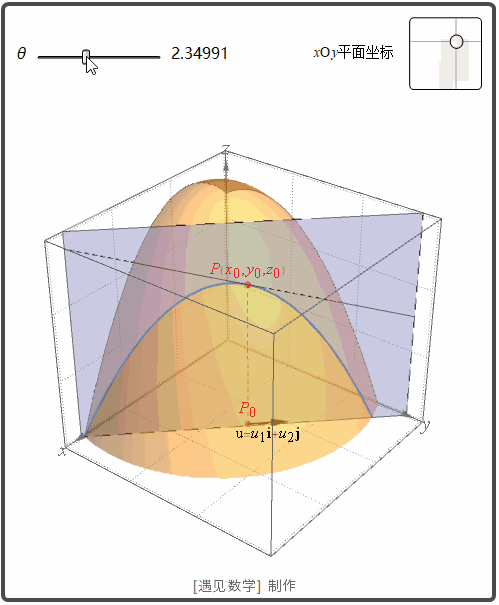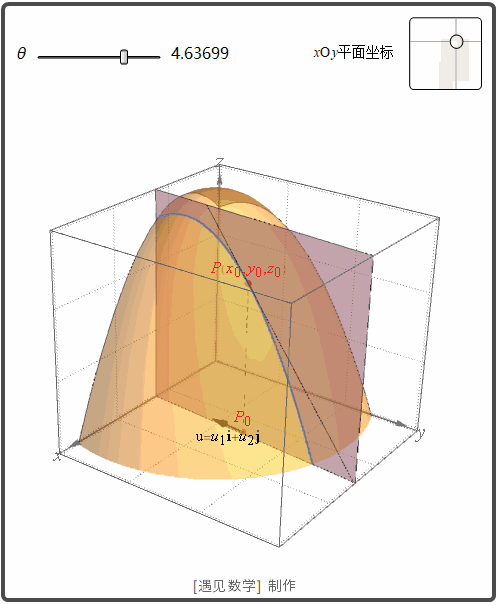
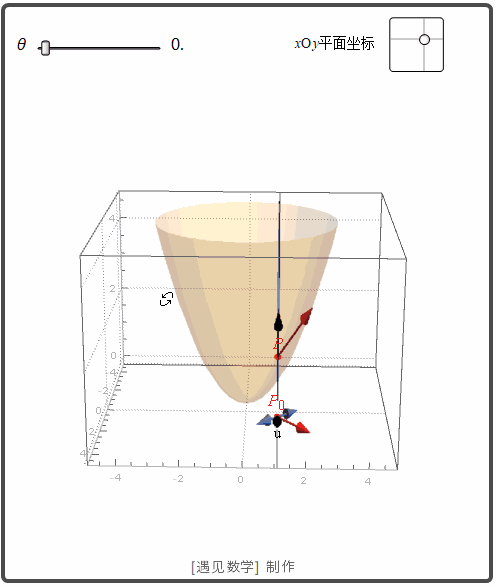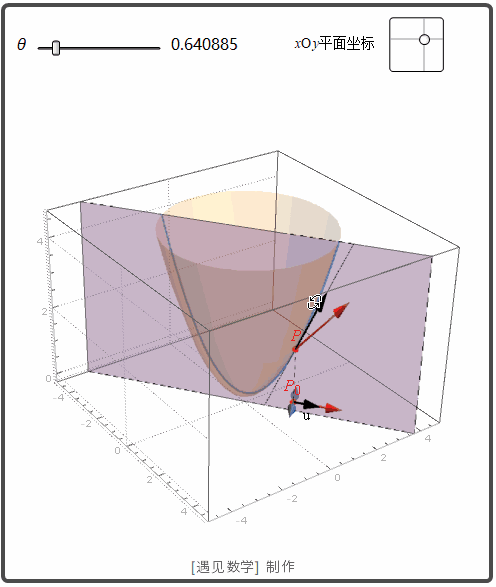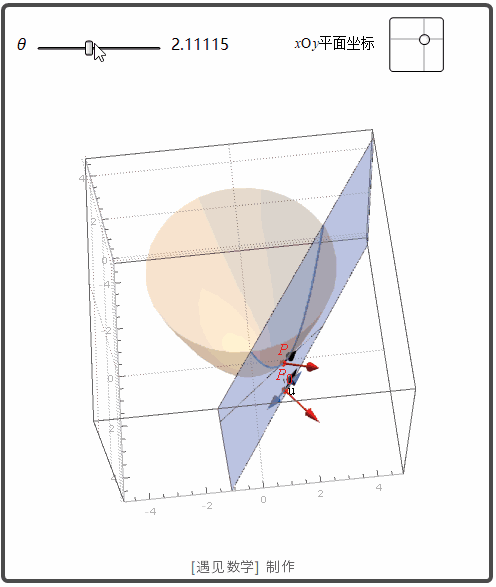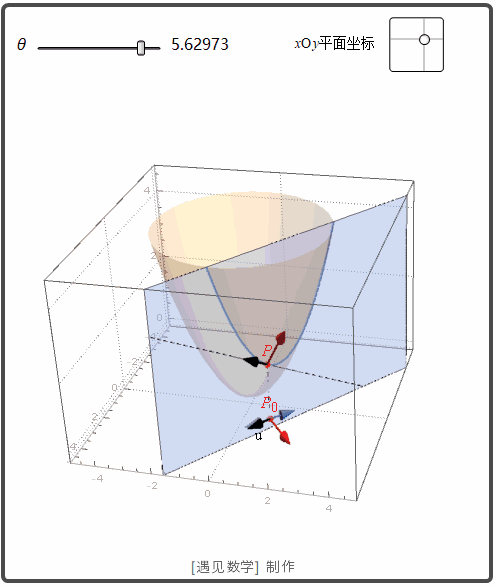
函数 z=f(x,y) 表示空间曲面 S. 则点 P(x0, y0,z0)
P(
x
0
,
y
0
,
z
0
)
在 S 上. 过点 P 和 P0
P
0
的 u 方向的垂直平面交 S 与曲线 C. f 沿方向 u 的变化率是 C 在点 P 的切线的斜率. 观察下面动画:
![]()
方向导数推广了两个偏导数, 现在可以求沿任何方向的变化率了.
计算
![]()
一个更有效的计算 f 在 P0
cbf;
P
0
方向 u 的方向导数的公式,就是 u 与 f 在 P0
P
0
梯度的点击.
![]()
方向导数的性质
根据上式, 当 cosθ=1
cos
θ
=1
时, u 与 ▽f 同方向时, 函数 f 增加最快, 类似, 反方向减少最快. 而正交于梯度的方式 u 是 f 变化率为 0 的方向, 此时 θ=π/2.
函数 f(x) = x22+y22
f(x) =
x
2
2
+
y
2
2
在 (1,1) 增加最快的方向梯度的方向, 它对应于在点 (1,1,1) 在曲面上最陡峭的方向.
![]()
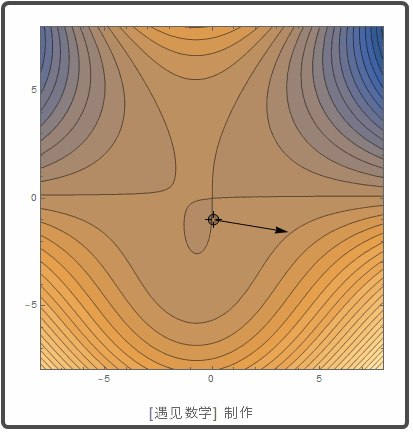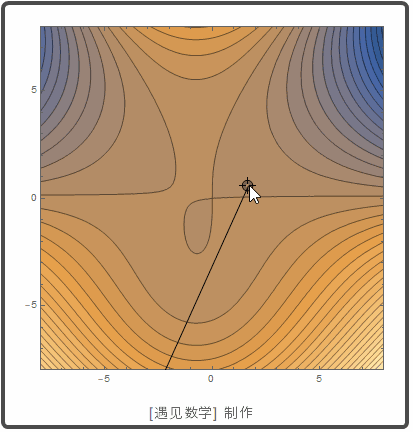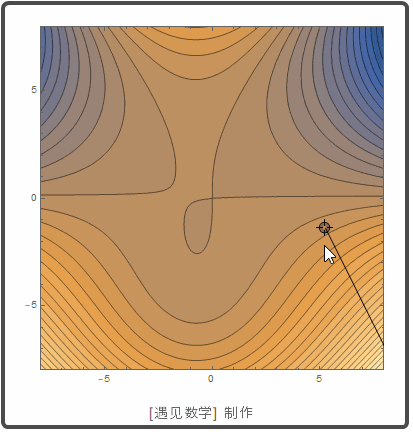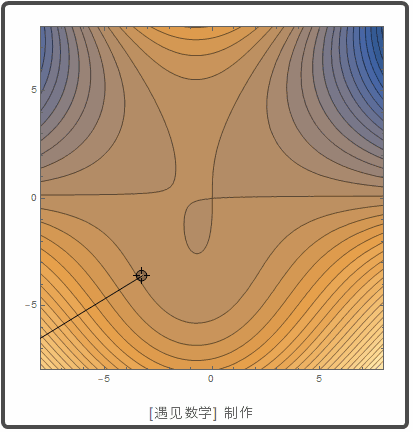
梯度和等高线的切线
函数 f(x,y) 的定义域的每个点 (x0,y0)
(
x
0
,
y
0
)
, f 的梯度正交于过 (x0,y0)
(
x
0
,
y
0
)
的等高线.
创建互动等高线,把法线显示为一个点:
![]()
增量和距离
f 沿方向 u 的变化有多少, 如从点 P0
P
0
沿 u 移动一点点距离 ds , f 的值变化多少等于方向导数乘以ds .
三元函数
现在再看三元可微函数 f(x,y,z), 与之对应的单位向量 u=⟨u1,u2,u3⟩ 则
![]()
切平面和法线
三元可微函数 f(x,y,z) 的梯度向量满足二元函数梯度的所有性质.
![]()
观察下面 "-17+x+2 y+4 z=0" 的等位面上的切平面动画:
![]()
(完)
「予人玫瑰, 手留余香」
转发既是支持, 我们会努力走得更远!