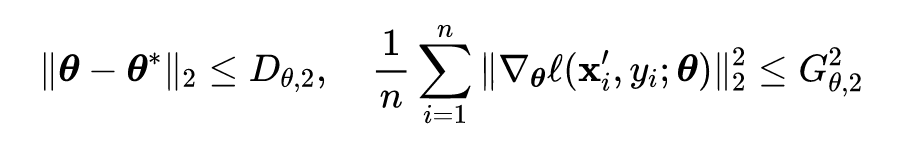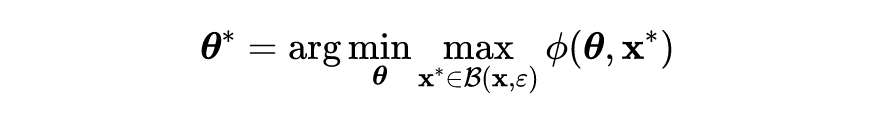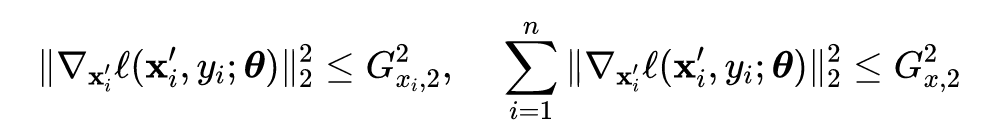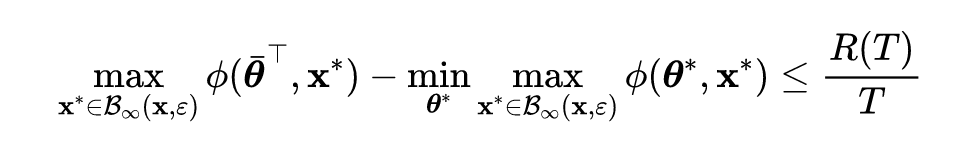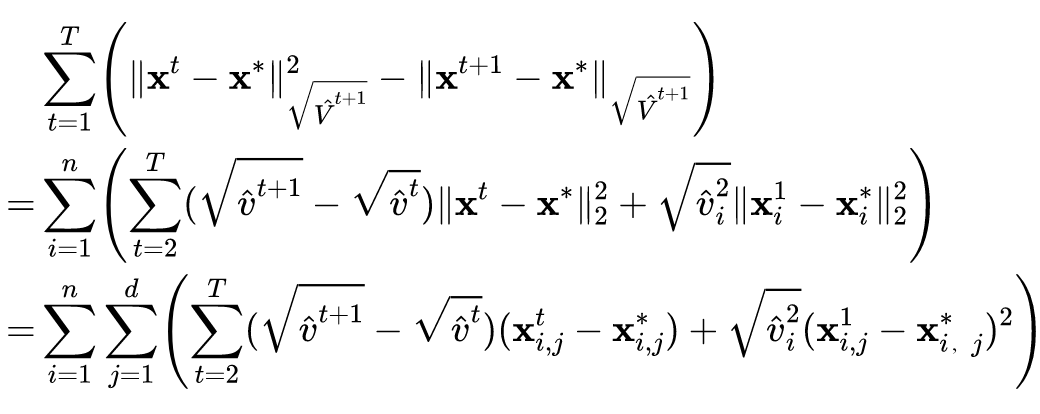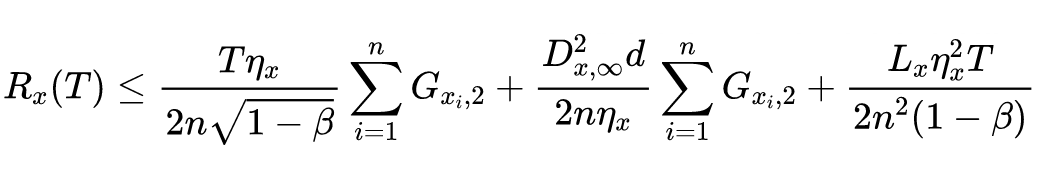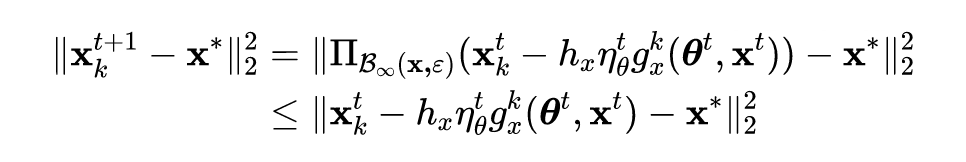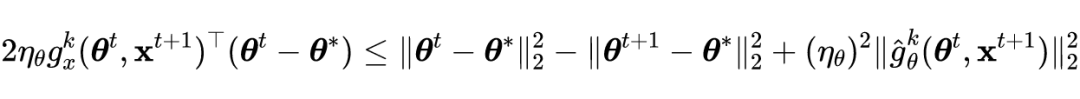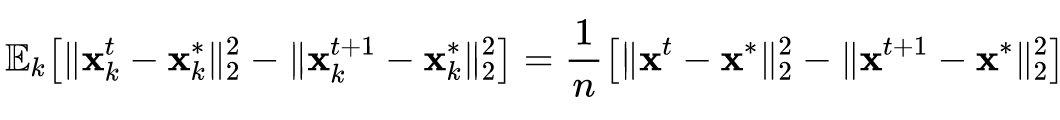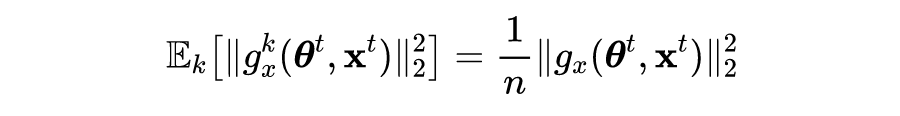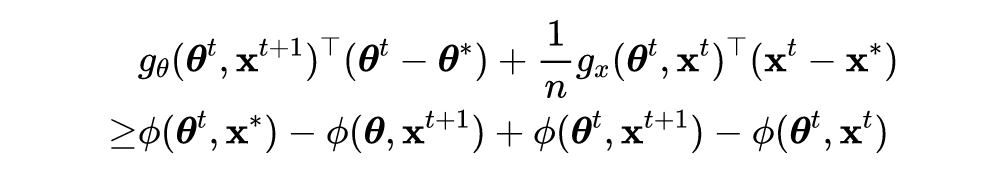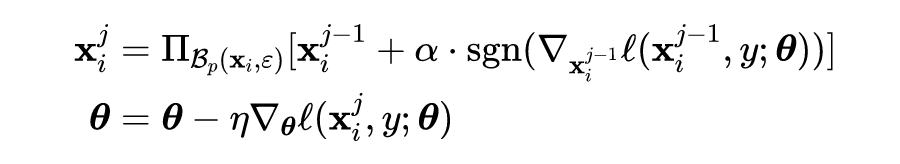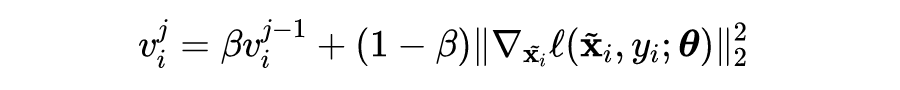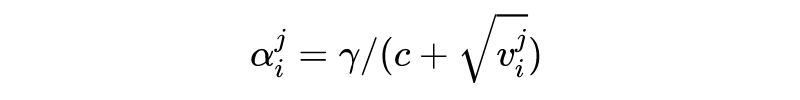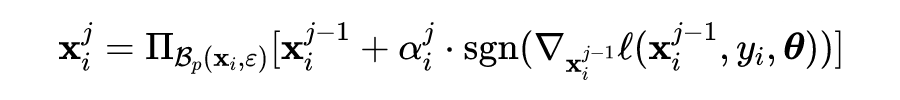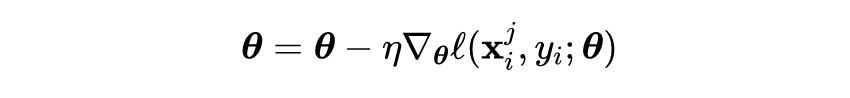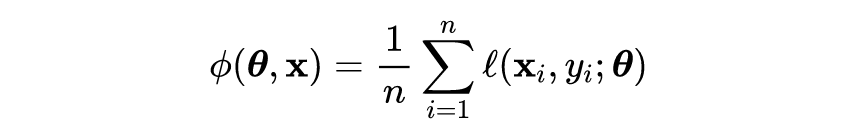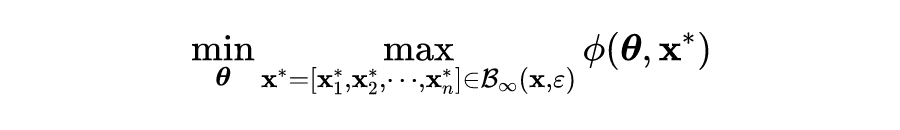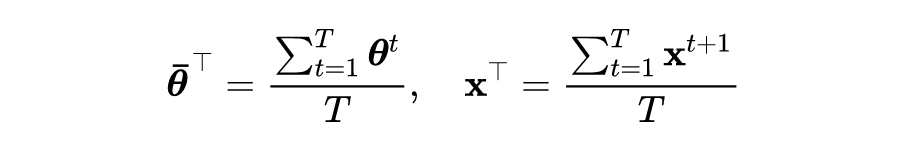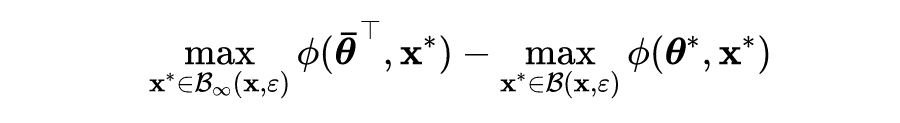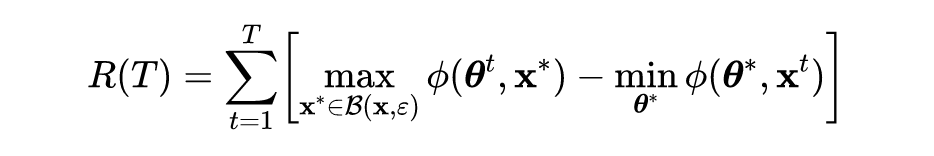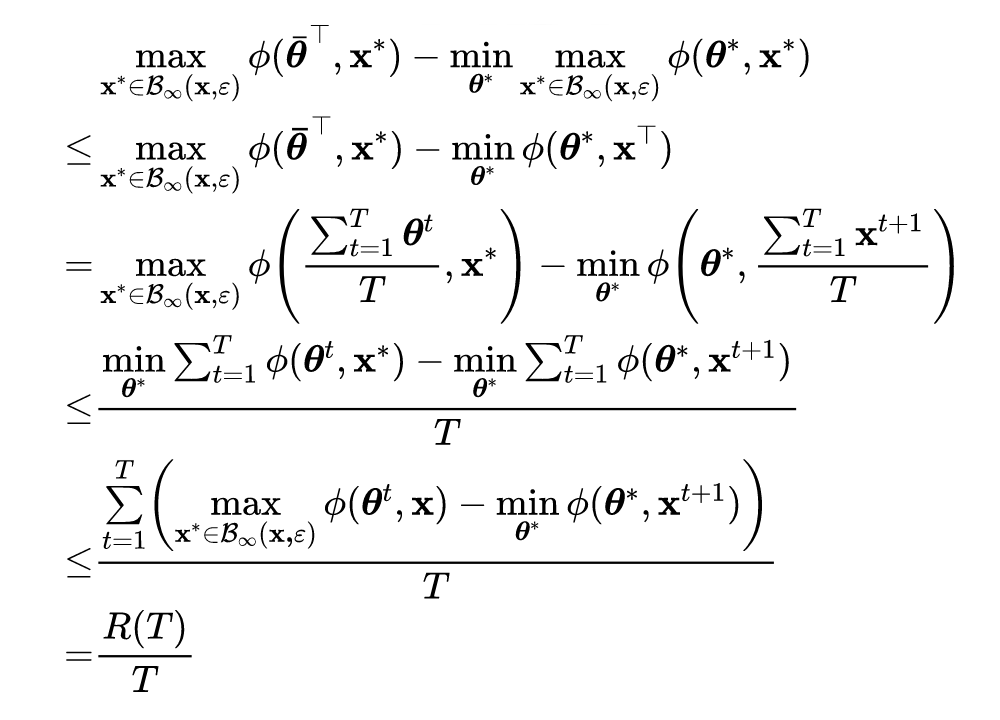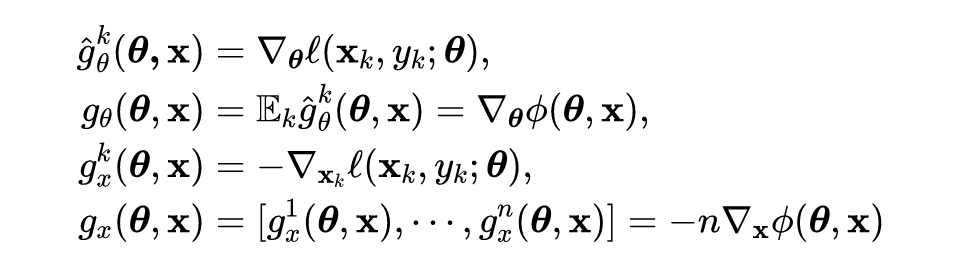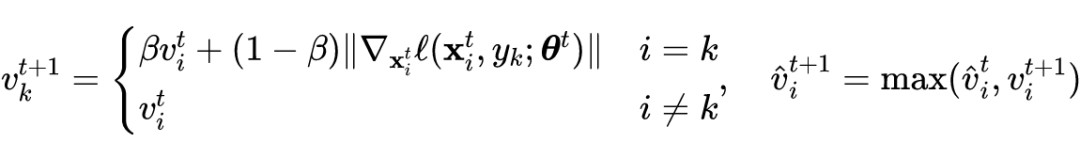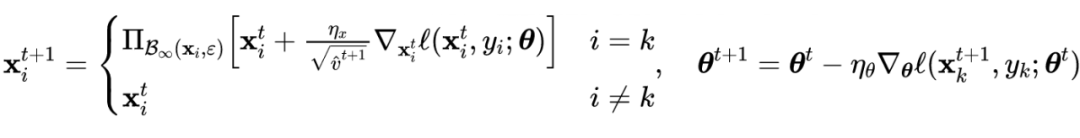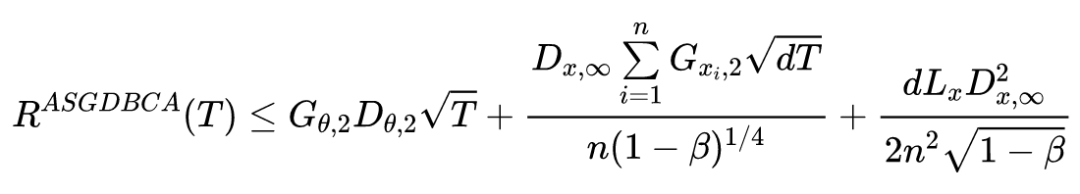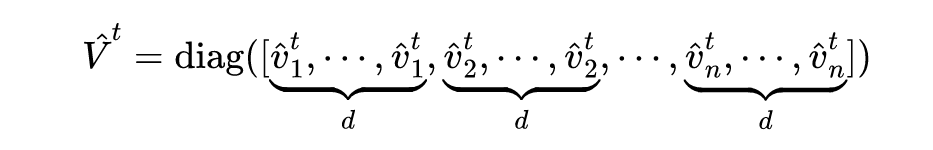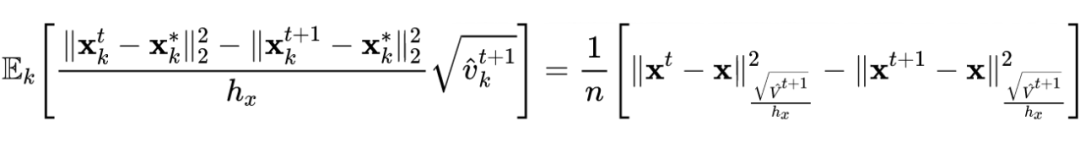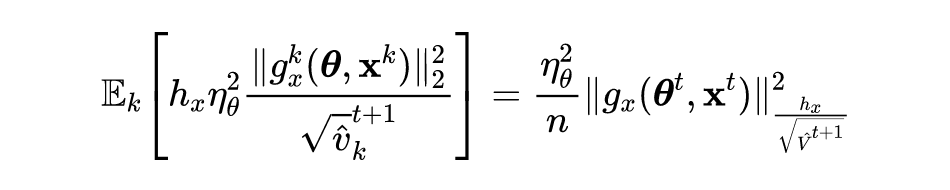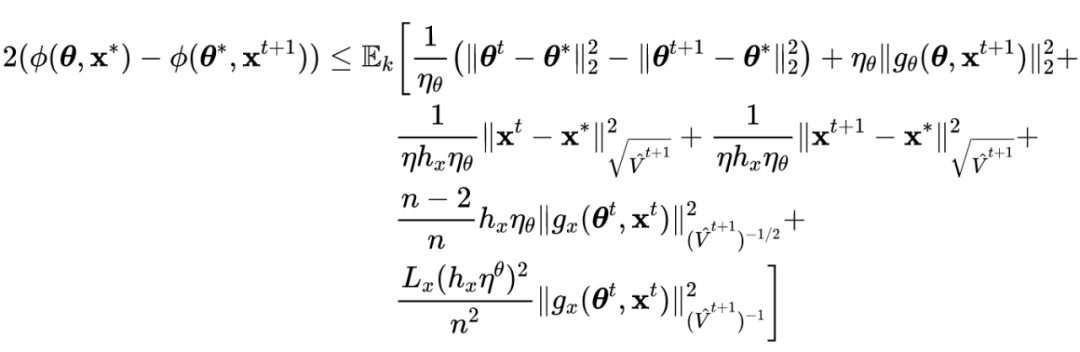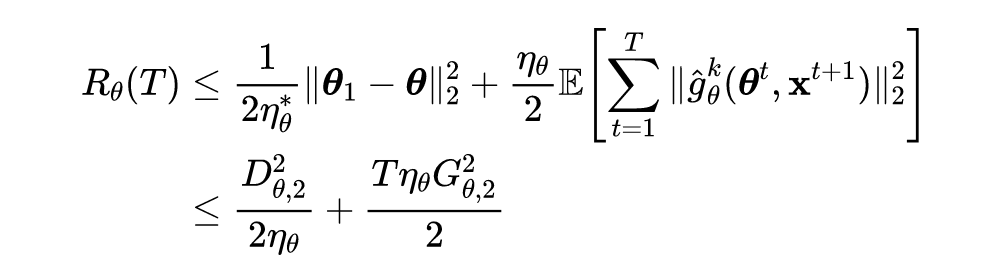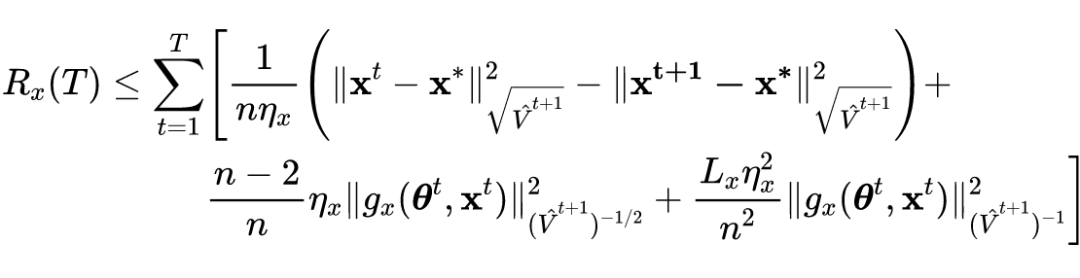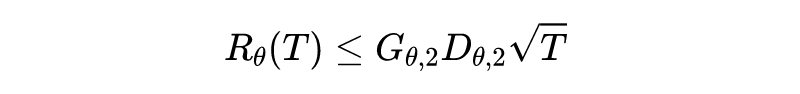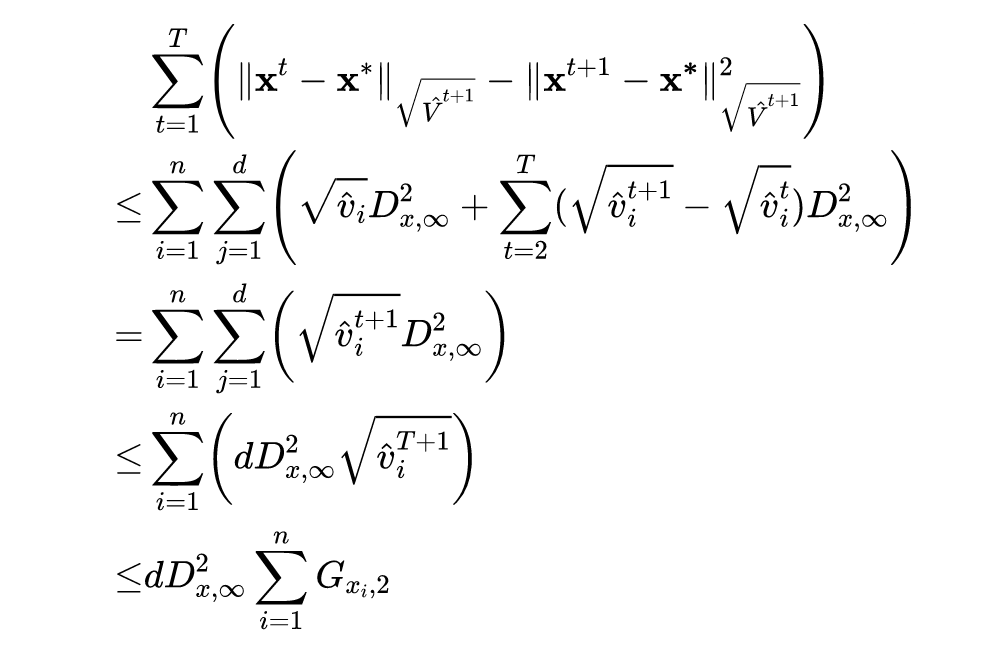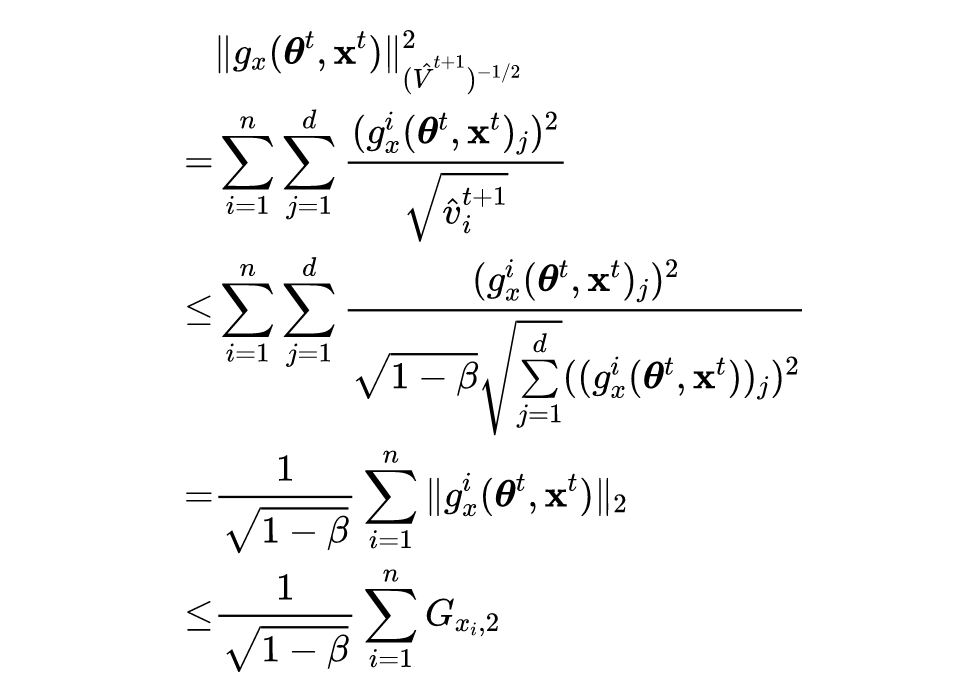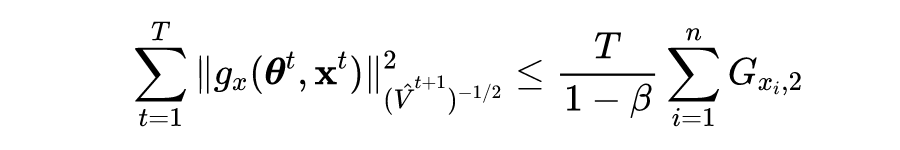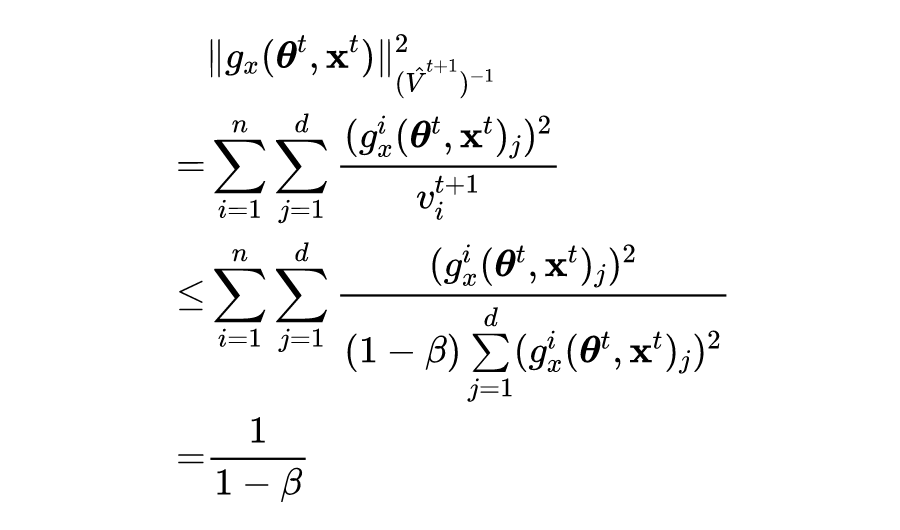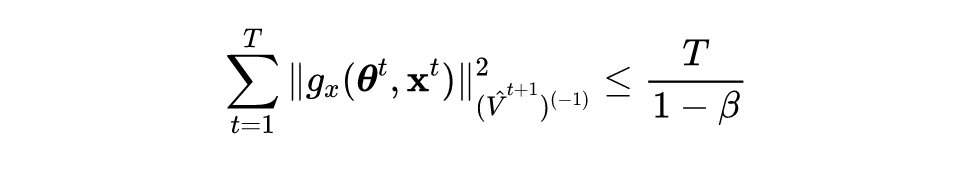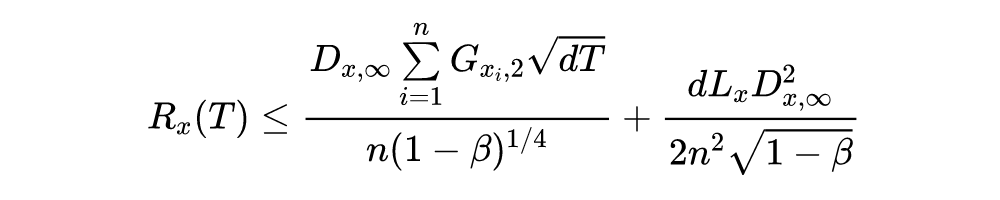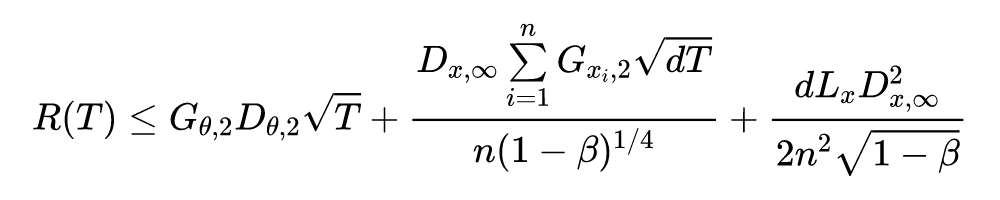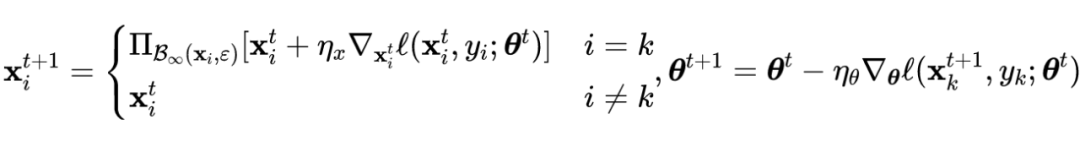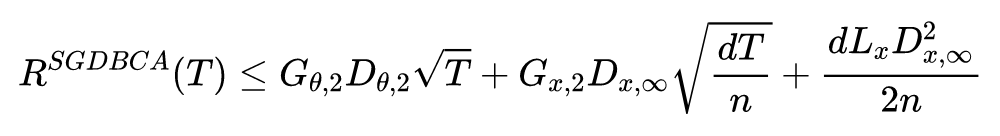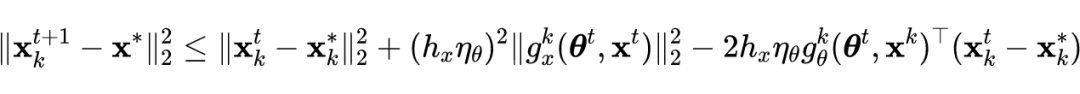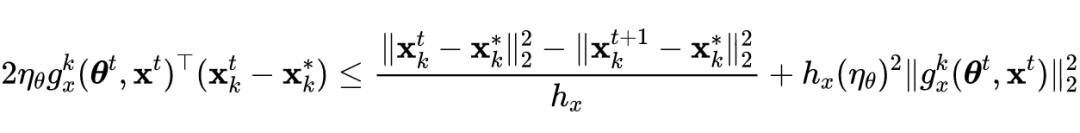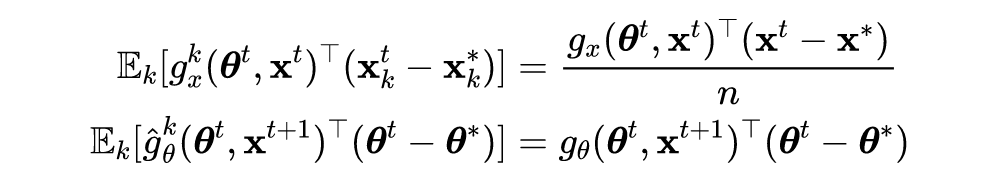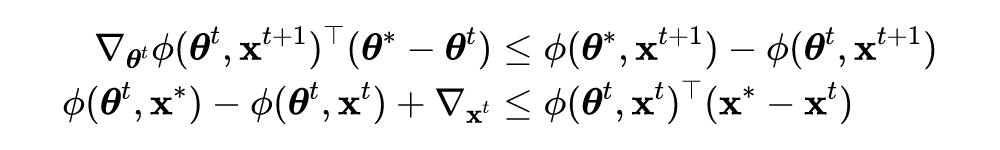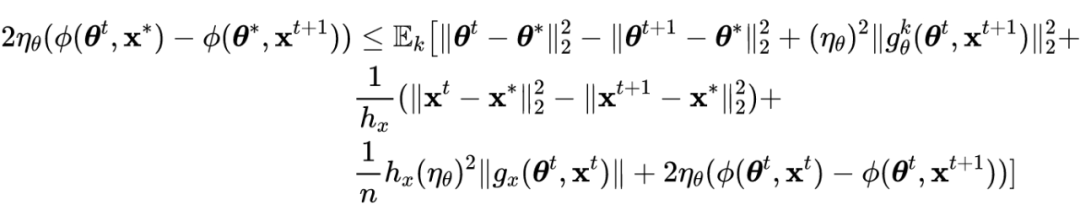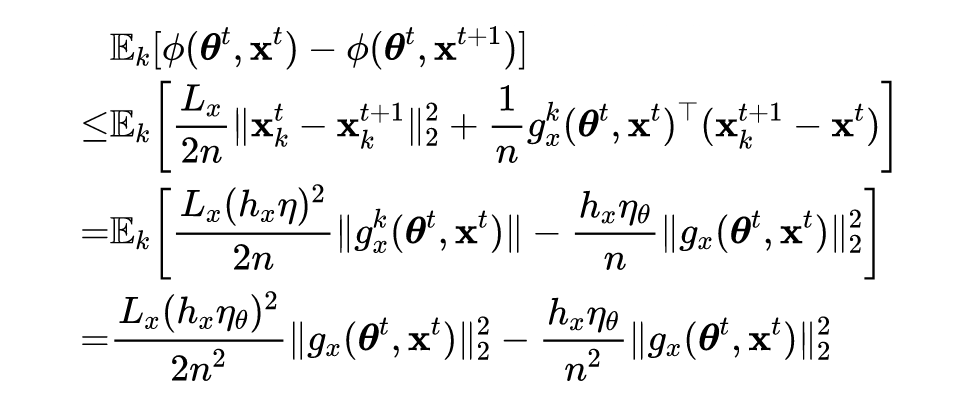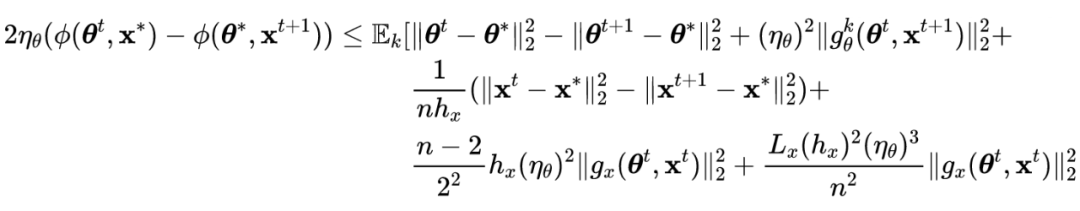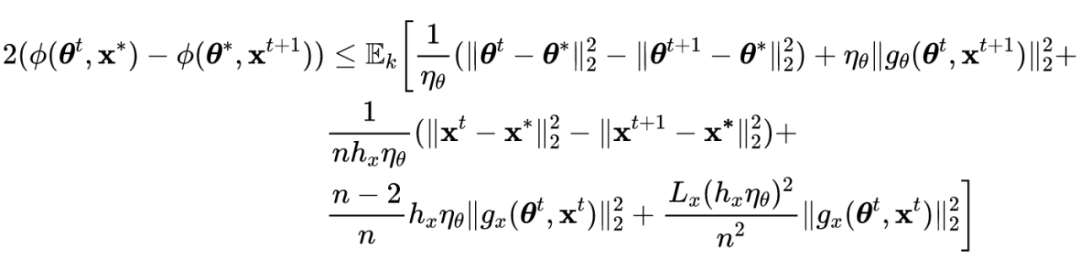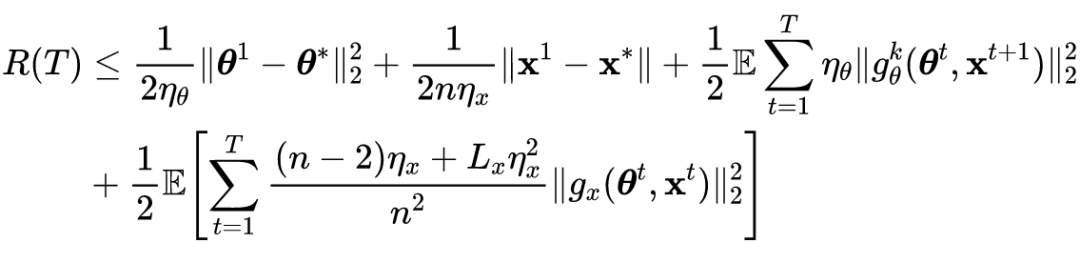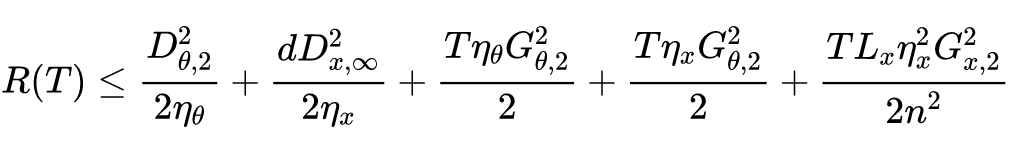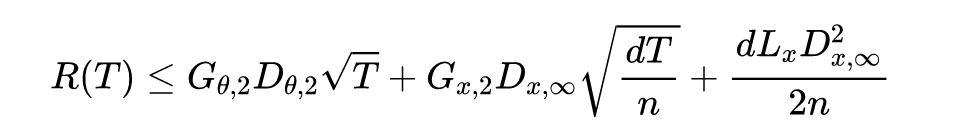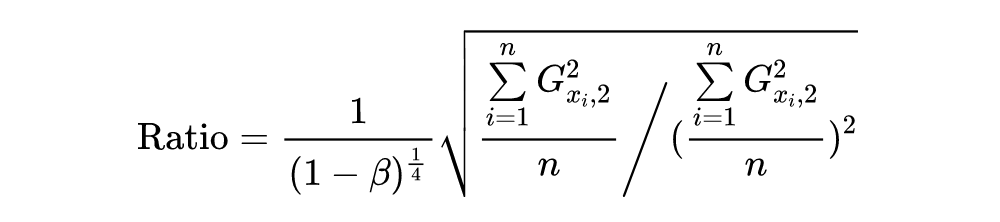![]()
©PaperWeekly 原创 · 作者 | 鬼谷子
引言
该论文是关于对抗训练理论分析性的文章,目前对抗训练及其变体已被证明是抵御对抗攻击的最有效防御手段,但对抗训练的过程极其缓慢使其难以扩展到像 ImageNet 这样的大型数据集上,而且在对抗训练的过程中经常会出现模型过拟合现象。在该论文中,作者从训练样本的角度研究了这一现象,研究表明模型过拟合现象是依赖于训练样本,并且具有较大梯度范数的训练样本更有可能导致灾难性过拟合。因此,作者提出了一种简单但有效的方法,即自适应步长对抗训练 (ATAS)。
ATAS 学习调整与其梯度范数成反比的训练样本自适应步长。理论分析表明,ATAS 比常用的非自适应算法收敛得更快,在对各种对抗扰动进行评估时,ATAS 始终可以减轻模型的过拟合现象,并且该算法在 CIFAR10、CIFAR100和ImageNet 等数据集上实现更高的模型鲁棒性。
![]()
Fast Adversarial Training with Adaptive Step Size
论文链接:
https://arxiv.org/abs/2206.02417
FreeAT 首先提出了一种快速对抗训练的方法,通过批量重复训练并同时优化模型参数和对抗扰动。YOPO 采用了类似的策略来优化对抗损失函数。后来,单步法被证明比 FreeAT 和 YOPO 更有效。如果仔细调整超参数,带随机启动的 FGSM(FGSM-RS)可用于一步生成对抗扰动,来训练鲁棒网络模型。ATTA 方法则是利用对抗样本的可迁移性,使用干净样本作为对抗样本的初始化,具体的优化形式如下所示:
![]()
其中,
表示在第
轮中第
个样本
生成的对抗样本。ATTA 显示出与 FGSM-RS 相当的鲁棒精度。SLAT 与 FGSM 同时扰动输入和潜在值,确保更可靠的性能。这些单步方法会产生灾难性的过拟合现象,这意味着模型对 PGD 攻击的鲁棒性精度会突然下降到接近 0,而对 FGSM 攻击的鲁棒精度迅速提高。
为了防止模型过拟合现象,FGSM-GA 添加了一个正则化器,用于对齐输入梯度的方向。另一项工作从损失函数的角度研究这一现象,发现模型过度现象是损失面高度扭曲的结果,并提出了一种通过沿梯度方向检查损失值来解决模型过拟合的新算法。然而,这两种算法都需要比 FGSM-RS 和 ATTA 更多的计算量。
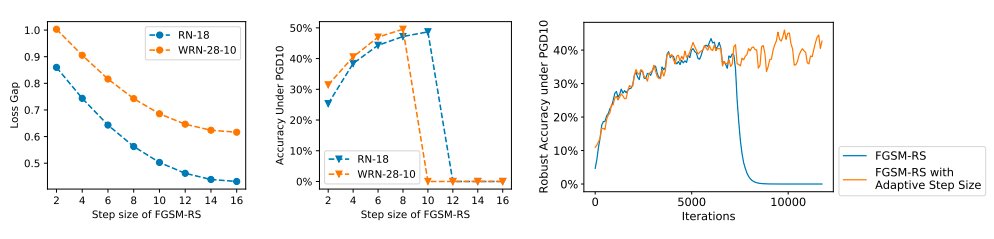
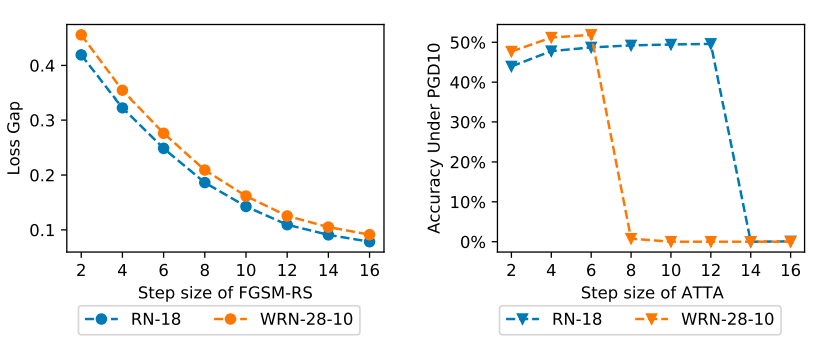
由之前的研究可知,对抗训练目标函数中内部最大化的步长对单步攻击方法的性能起着重要作用。过大的步长会将所有 FGSM 对抗扰动吸引到分类边界附近,导致灾难性过拟合现象,因此 PGD 多步攻击下的分类器对抗鲁棒性精度将降至零。然而,又不能简单地减小步长,因为如下图的第一张图和第二张图所示可以发现,增大步长可以增强对抗攻击并且能提高模型鲁棒性。
为了尽可能加强攻击并避免灾难性的过拟合现象,对于具有大梯度范数的样本,作者使用小步长来加强攻击防止模型过拟合现象;对于具有小梯度范数的样本,作者使用大步长来加强攻击。所以,作者使用梯度范数的移动平均值:
![]()
去调整在第
轮中对于样本
的步长
。
是
的初始化,
是动量平衡因子。
与
成反比例:
![]()
其中
是预定义的学习率,
是一个防止
过大的常数。作者将自适应步长
与 FGSM-RS 相结合,FGSM-RS 在内部最大化攻击中随机初始化对抗扰动。由上图的第三张子图可以发现,自适应步长不会发生过拟合现象。此外,自适应步长方法的平均步长甚至比 FGSM-RS 中的固定步长还要大,因此具有更强的攻击性和更好的对抗鲁棒性。
随机初始化限制了步长较小的样本的对抗扰动,从而削弱了对抗攻击的强度。结合之前的初始化方法,论文提出的方法 ATAS 不需要大的
来达到整个
范数球。对于每个样本,作者使用自适应步长
并执行以下内部最大化以获得对抗样本:
![]()
其中
是第
轮的对抗样本,参数
由样本
来更新,具体公式如下所示:
![]()
与以前需要大量计算开销来解决灾难性过拟合现象问题的方法相比,论文提出的 ATAS 方法的开销可以忽略不计,ATAS 的训练时间与 ATTA 和 FGSM-RS 几乎相同。ATAS 的详细算法如下所示:
![]()
在 ImageNet 数据集上 ATAS 的详细算法如下所示:
![]()
作者分析论文中 ATAS 方法在
范数下的收敛性,给定如下目标函数:
![]()
![]()
其中
为在参数
下的最优对抗样本。作者考虑最小最大优化问题是在凸凹和平滑的设定下,并且损失函数
满足以下假设。
1)
是凸函数并且
在参数
下是平滑的;
和
的梯度在
范数满足如下公式:
2)
是凹函数并且
在每个样本
平滑。
在
范数球内并且半径为
。对于任意
和
,
,并且输入梯度满足如下公式:
![]()
![]()
![]()
引理1:损失函数
满足假设 1,目标函数
有如下收敛间隙不等式:
证
明:
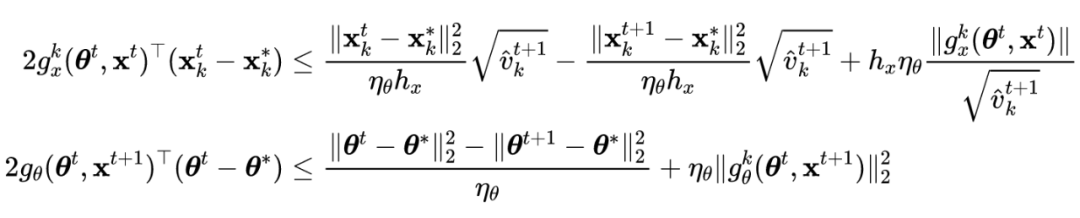
根据引理 1 公式的左侧可得如下不等式:
![]()
第一个和第三个不等式遵循最优性条件,第二个不等式使用 Jensen 不等式。在证明定理 1 和定理 2 时,有以下几个梯度符号:
![]()
ATAS 方法也可以表示为自适应随机梯度下降块坐标上升法(ASGDBCA),在步骤
中随机选取一个样本
,对参数
应用随机梯度下降,对输入
应用自适应块坐标上升。与 SGDA 不同,SGDA 在每次迭代中更新
的所有维度,ASGDBCA 只更新
的一些维度。ASGDBCA 首先计算预调节参数
为:
![]()
则
和
可以被优化为:
![]()
ASGDBCA 和 ATAS 的主要差异为
。为了证明 ASGDBCA 的收敛性,前置调节参数必须是非递减的。否则,ATAS 可能不会像 ADAM 那样收敛。然而,ADAM 的非收敛版本实际上在实际中对神经网络更有效。因此,ATAS 仍然使用
作为预调节参数。
定理1:在假设 1 条件下,有
和
,则 ASGDBA 的界为如下公式所示:
![]()
证明:
令
,在第
步时,ASGDBCA 从
中随机采样下标索引为
的样本,于是则有:
![]()
令:
![]()
表示为样本
的所有坐标预调整参数。将期望值置于右侧的
之上,于是则有:
![]()
![]()
与 SGDBCA 的证明过程类似,有如下推导过程:
![]()
将不等式从
求和到
,
的上界表示为:
![]()
![]()
与 SGD 相似,使用算术和几何均值不等式可知,当
时达到最优,于是则有:
![]()
![]()
其中
表示
中第
个坐标。对
项进行求和,
的第二项的上界为:
![]()
![]()
![]()
使用算术和几何均值不等式可知,当
时,上界可以达到最小值:
![]()
![]()
ATAS 和 ATTA 的非自适应版本的随机梯度下降块坐标上升的公式如下所示:
![]()
定理2
:在假设 1 的条件下,常数学习率
和
,则 SGDBCA 的上界为如下所示:
![]()
证明:
令
,在第
步时,SGDBCA 从下标索引集合
中随机采样出下标
的样本并更新对抗扰动,则有以下不等式:
![]()
![]()
相似的可以得到:
将以上两个公式左边部分求期望可以得到:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
使用算术和几何平均值可以得到,当
和
是,可以得到最优上界:
![]()
定理 1 和 2 表明 ASGDBCA 比 SGDBCA 收敛更快。当
较大时,SGDBCA 和 ASGDBCA 中的间隔的第三项可以忽略不计。考虑到它们的第一项是相同的,主要区别是第二项中
和 关于
间隔界。它们的比率为如下所示:
![]()
Cauchy-Schwarz 不等式表明该比率始终大于 1。当
具有长尾分布时,ASGDBCA 和 SGDBCA 之间的差距会变得更大,这表明 ATAS 的收敛速度相对更快。
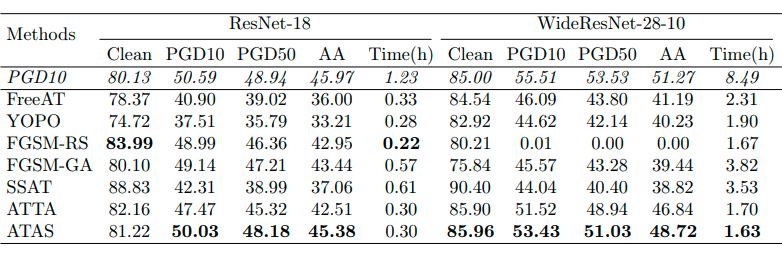
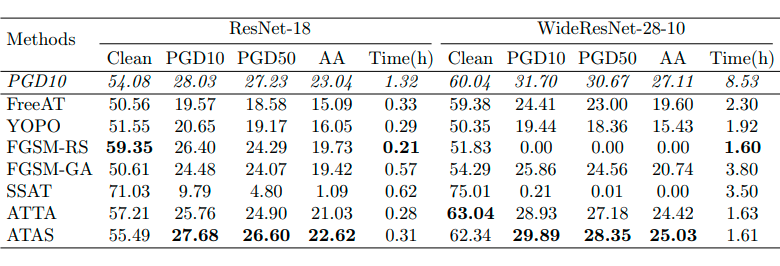
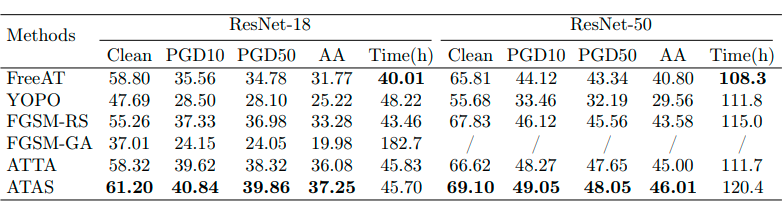
以下三个表格分别显示了不同方法在 CIFAR10、CIFAR100 和 ImageNet 数据集上的准确性和训练时间。需要注意的是,由于计算复杂性,作者没有足够的计算资源在 ImageNet 上执行标准对抗训练和 SSAT。作者使用两个 GPU 来训练 ImageNet 的模型,对于 CIFAR10 和 CIFAR100,作者在单个 GPU 上评估训练时间。从以下结果可以直观的发现论文中提出的方法 ATAS 提高了在各种攻击(包括 PGD10、PGD50 和自动攻击)下的分类模型的鲁棒性,并且可以发现在训练中避免发生模型灾难性过拟合现象。
![]()
![]()
![]()
如下图所示,可以发现等当增加 ATTA 中的训练步长时,ATTA 和 PGD10 之间的损失函数的间隙会变小。此外,当步长不是太大的时候,分类模型的鲁棒精度会随着步长增加。进而可以得出初步结论,较大的步长也增强了 ATTA 的攻击能力。然而,大步长也会导致 ATTA 发生模型过拟合现象。
![]()
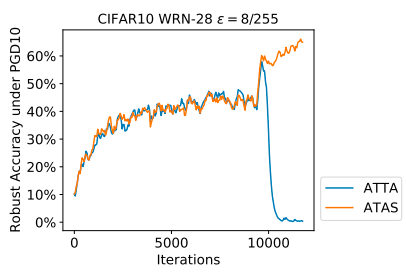
论文中的方法 ATAS 中的自适应步长允许更大的步长,而不会导致模型灾难性过拟合现象。如下图所示作者显示了 ATTA 和 ATAS 之间的比较。即使 ATAS 的步长大于 ATTA,它不会像 ATTA 那样出现模型过拟合现象。
![]()
![]()
![]()
如何才能让更多的优质内容以更短路径到达读者群体,缩短读者寻找优质内容的成本呢?答案就是:你不认识的人。
总有一些你不认识的人,知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁,促使不同背景、不同方向的学者和学术灵感相互碰撞,迸发出更多的可能性。
PaperWeekly 鼓励高校实验室或个人,在我们的平台上分享各类优质内容,可以是最新论文解读,也可以是学术热点剖析、科研心得或竞赛经验讲解等。我们的目的只有一个,让知识真正流动起来。
📝 稿件基本要求:
• 文章确系个人原创作品,未曾在公开渠道发表,如为其他平台已发表或待发表的文章,请明确标注
• 稿件建议以 markdown 格式撰写,文中配图以附件形式发送,要求图片清晰,无版权问题
• PaperWeekly 尊重原作者署名权,并将为每篇被采纳的原创首发稿件,提供业内具有竞争力稿酬,具体依据文章阅读量和文章质量阶梯制结算
📬 投稿通道:
• 投稿邮箱:hr@paperweekly.site
• 来稿请备注即时联系方式(微信),以便我们在稿件选用的第一时间联系作者
• 您也可以直接添加小编微信(pwbot02)快速投稿,备注:姓名-投稿
![]()
△长按添加PaperWeekly小编
🔍
现在,在「知乎」也能找到我们了
进入知乎首页搜索「PaperWeekly」
点击「关注」订阅我们的专栏吧
![]()