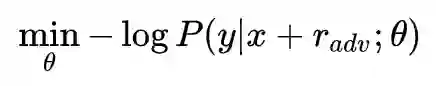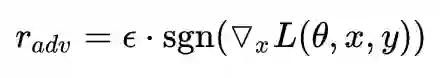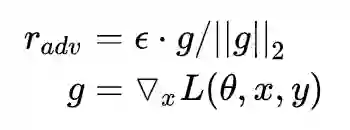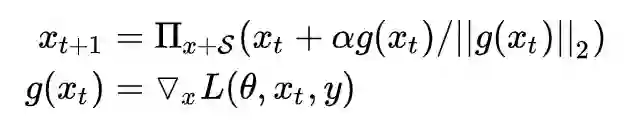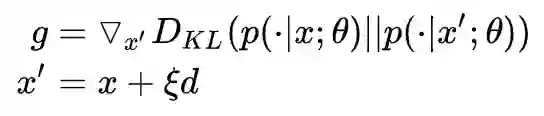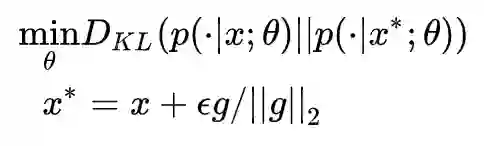训练技巧 | 功守道:NLP中的对抗训练 + PyTorch实现
作者丨Nicolas
单位丨追一科技AI Lab研究员
研究方向丨信息抽取、机器阅读理解
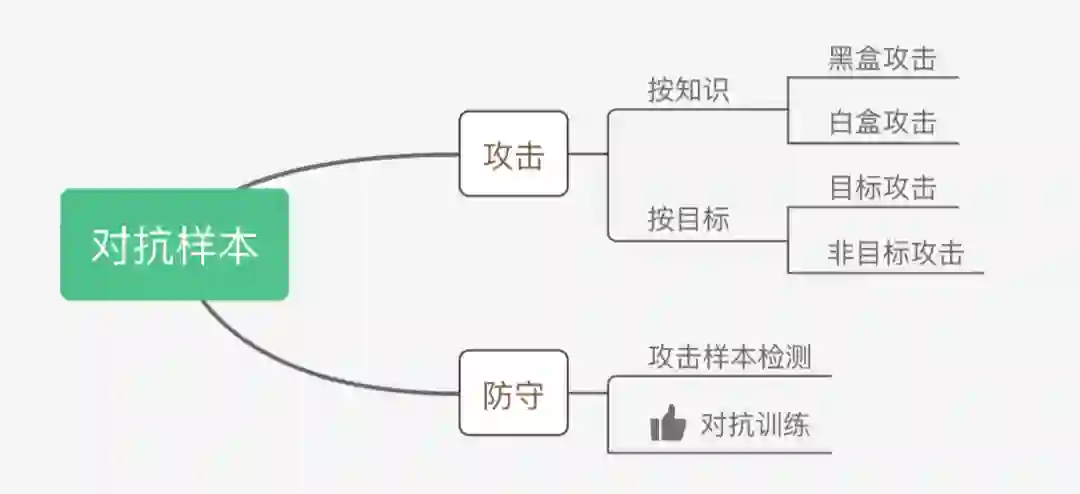
对抗样本
对抗训练的基本概念
Min-Max公式
从CV到NLP
Because the set of high-dimensional one-hot vectors does not admit infinitesimal perturbation, we define the perturbation on continuous word embeddings instead of discrete word inputs.
NLP中的两种对抗训练 + PyTorch实现
Fast Gradient Method(FGM)
上面我们提到,Goodfellow 在 15 年的 ICLR [7] 中提出了 Fast Gradient Sign Method(FGSM),随后,在 17 年的 ICLR [9] 中,Goodfellow 对 FGSM 中计算扰动的部分做了一点简单的修改。假设输入的文本序列的 embedding vectors 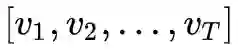
实际上就是取消了符号函数,用二范式做了一个 scale,需要注意的是:这里的 norm 计算的是,每个样本的输入序列中出现过的词组成的矩阵的梯度 norm。原作者提供了一个 TensorFlow 的实现 [10],在他的实现中,公式里的 x 是 embedding 后的中间结果(batch_size, timesteps, hidden_dim),对其梯度 g 的后面两维计算 norm,得到的是一个 (batch_size, 1, 1) 的向量。
为了实现插件式的调用,笔者将一个 batch 抽象成一个样本,一个 batch 统一用一个 norm,由于本来 norm 也只是一个 scale 的作用,影响不大。笔者的实现如下:
import torch
class FGM():
def __init__(self, model):
self.model = model
self.backup = {}
def attack(self, epsilon=1., emb_name='emb.'):
# emb_name这个参数要换成你模型中embedding的参数名
for name, param in self.model.named_parameters():
if param.requires_grad and emb_name in name:
self.backup[name] = param.data.clone()
norm = torch.norm(param.grad)
if norm != 0 and not torch.isnan(norm):
r_at = epsilon * param.grad / norm
param.data.add_(r_at)
def restore(self, emb_name='emb.'):
# emb_name这个参数要换成你模型中embedding的参数名
for name, param in self.model.named_parameters():
if param.requires_grad and emb_name in name:
assert name in self.backup
param.data = self.backup[name]
self.backup = {}
需要使用对抗训练的时候,只需要添加五行代码:
# 初始化
fgm = FGM(model)
for batch_input, batch_label in data:
# 正常训练
loss = model(batch_input, batch_label)
loss.backward() # 反向传播,得到正常的grad
# 对抗训练
fgm.attack() # 在embedding上添加对抗扰动
loss_adv = model(batch_input, batch_label)
loss_adv.backward() # 反向传播,并在正常的grad基础上,累加对抗训练的梯度
fgm.restore() # 恢复embedding参数
# 梯度下降,更新参数
optimizer.step()
model.zero_grad()
PyTorch 为了节约内存,在 backward 的时候并不保存中间变量的梯度。因此,如果需要完全照搬原作的实现,需要用 register_hook 接口 [11] 将 embedding 后的中间变量的梯度保存成全局变量,norm 后面两维,计算出扰动后,在对抗训练 forward 时传入扰动,累加到 embedding 后的中间变量上,得到新的 loss,再进行梯度下降。不过这样实现就与我们追求插件式简单好用的初衷相悖,这里就不赘述了,感兴趣的读者可以自行实现。
Projected Gradient Descent(PGD)
内部 max 的过程,本质上是一个非凹的约束优化问题,FGM 解决的思路其实就是梯度上升,那么 FGM 简单粗暴的“一步到位”,是不是有可能并不能走到约束内的最优点呢?当然是有可能的。于是,一个很 intuitive 的改进诞生了:Madry 在 18 年的 ICLR 中 [8],提出了用 Projected Gradient Descent(PGD)的方法,简单的说,就是“小步走,多走几步”,如果走出了扰动半径为 ϵ 的空间,就映射回“球面”上,以保证扰动不要过大:
其中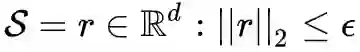
import torch
class PGD():
def __init__(self, model):
self.model = model
self.emb_backup = {}
self.grad_backup = {}
def attack(self, epsilon=1., alpha=0.3, emb_name='emb.', is_first_attack=False):
# emb_name这个参数要换成你模型中embedding的参数名
for name, param in self.model.named_parameters():
if param.requires_grad and emb_name in name:
if is_first_attack:
self.emb_backup[name] = param.data.clone()
norm = torch.norm(param.grad)
if norm != 0 and not torch.isnan(norm):
r_at = alpha * param.grad / norm
param.data.add_(r_at)
param.data = self.project(name, param.data, epsilon)
def restore(self, emb_name='emb.'):
# emb_name这个参数要换成你模型中embedding的参数名
for name, param in self.model.named_parameters():
if param.requires_grad and emb_name in name:
assert name in self.emb_backup
param.data = self.emb_backup[name]
self.emb_backup = {}
def project(self, param_name, param_data, epsilon):
r = param_data - self.emb_backup[param_name]
if torch.norm(r) > epsilon:
r = epsilon * r / torch.norm(r)
return param_data + r
def backup_grad(self):
for name, param in self.model.named_parameters():
if param.requires_grad:
self.grad_backup[name] = param.grad
def restore_grad(self):
for name, param in self.model.named_parameters():
if param.requires_grad:
param.grad = self.grad_backup[name]
使用的时候,要麻烦一点:
pgd = PGD(model)
K = 3
for batch_input, batch_label in data:
# 正常训练
loss = model(batch_input, batch_label)
loss.backward() # 反向传播,得到正常的grad
pgd.backup_grad()
# 对抗训练
for t in range(K):
pgd.attack(is_first_attack=(t==0)) # 在embedding上添加对抗扰动, first attack时备份param.data
if t != K-1:
model.zero_grad()
else:
pgd.restore_grad()
loss_adv = model(batch_input, batch_label)
loss_adv.backward() # 反向传播,并在正常的grad基础上,累加对抗训练的梯度
pgd.restore() # 恢复embedding参数
# 梯度下降,更新参数
optimizer.step()
model.zero_grad()
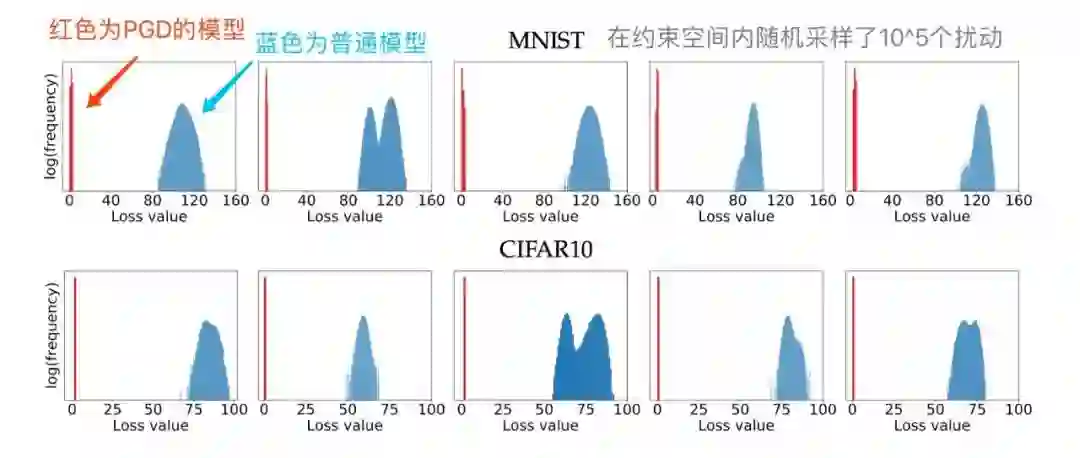
在 [8] 中,作者将这一类通过一阶梯度得到的对抗样本称之为“一阶对抗”,在实验中,作者发现,经过 PGD 训练过的模型,对于所有的一阶对抗都能得到一个低且集中的损失值,如下图所示:
我们可以看到,面对约束空间 S 内随机采样的十万个扰动,PGD 模型能够得到一个非常低且集中的 loss 分布,因此,在论文中,作者称 PGD 为“一阶最强对抗”。也就是说,只要能搞定 PGD 对抗,别的一阶对抗就不在话下了。
实验对照
为了说明对抗训练的作用,笔者选了四个 GLUE 中的任务进行了对照试验。实验代码是用的 Huggingface 的 transfomers/examples/run_glue.py [12],超参都是默认的,对抗训练用的也是相同的超参。
我们可以看到,对抗训练还是有效的,在 MRPC 和 RTE 任务上甚至可以提高三四个百分点。不过,根据我们使用的经验来看,是否有效有时也取决于数据集。毕竟:缘,妙不可言~
总结
这篇博客梳理了 NLP 对抗训练发展的来龙去脉,介绍了对抗训练的数学定义,并对于两种经典的对抗训练方法,提供了插件式的实现,做了简单的实验对照。由于笔者接触对抗训练的时间也并不长,如果文中有理解偏差的地方,希望读者不吝指出。
一个彩蛋:Virtual Adversarial Training
除了监督训练,对抗训练还可以用在半监督任务中,尤其对于 NLP 任务来说,很多时候输入的无监督文本多的很,但是很难大规模地进行标注,那么就可以参考 [13] 中提到的 Virtual Adversarial Training 进行半监督训练。
首先,我们抽取一个随机标准正态扰动(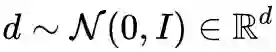
然后,用得到的梯度,计算对抗扰动,并进行对抗训练:
实现方法跟 FGM 差不多,这里就不给出了。
Reference
点击以下标题查看更多往期内容:

让你的论文被更多人看到
如何才能让更多的优质内容以更短路径到达读者群体,缩短读者寻找优质内容的成本呢?答案就是:你不认识的人。
总有一些你不认识的人,知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁,促使不同背景、不同方向的学者和学术灵感相互碰撞,迸发出更多的可能性。
PaperWeekly 鼓励高校实验室或个人,在我们的平台上分享各类优质内容,可以是最新论文解读,也可以是学习心得或技术干货。我们的目的只有一个,让知识真正流动起来。
📝 来稿标准:
• 稿件确系个人原创作品,来稿需注明作者个人信息(姓名+学校/工作单位+学历/职位+研究方向)
• 如果文章并非首发,请在投稿时提醒并附上所有已发布链接
• PaperWeekly 默认每篇文章都是首发,均会添加“原创”标志
📬 投稿邮箱:
• 投稿邮箱:hr@paperweekly.site
• 所有文章配图,请单独在附件中发送
• 请留下即时联系方式(微信或手机),以便我们在编辑发布时和作者沟通
🔍
现在,在「知乎」也能找到我们了
进入知乎首页搜索「PaperWeekly」
点击「关注」订阅我们的专栏吧
关于PaperWeekly
PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域,欢迎在公众号后台点击「交流群」,小助手将把你带入 PaperWeekly 的交流群里。
▽ 点击 | 阅读原文 | 获取最新论文推荐