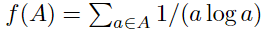导师震惊！26岁牛津数学博士成功破解质数猜想

---

  新智元报道  

编辑：LRS

【新智元导读】每攻克一个质数相关的猜想，背后都是数学家几十年的努力。最近一位26岁的牛津大学数学博士灵光一现，成功破解三十四年前的质数猜想，导师得知消息表示非常震惊！

在大于1的自然数中，除了1和该数自身外，无法被其他自然数整除的数，都称为 质数 （Primer number），也叫素数。

 

由于其特殊的性质，质数一直是数学家和计算机科学家热衷的研究问题，围绕质数也产生了很多著名的数学猜想。

 

其中一个就是1988年提出的 厄多斯本原集猜想 （The Erdős Primitive Set Conjecture）

 

几十年来，数学家们在证明这个猜想上面付出巨大努力，在 非质数 的序列上对猜想结果不断得到证明，但离最终的证明还有一段距离。

 

2018年，Jared Duer Lichtman开始研究本原集猜想，当时也是他在达特茅斯学院读 本科 的最后一年。

 

 

毕业后，他就跑到牛津大学在James Maynard教授手底下读博，继续研究本原集猜想等质数问题。

 

Maynard也是数学界 著名狠人 ，读博的时候，别人开组会是挨骂；Maynard来开组会，导师称之为 合作 。

 

James Maynard

2013年5月， 张益唐 证明了 孪生素数猜想 ，存在无穷多个素数对相差都小于7000万，一举破解 百年数学难题 ，随后陶哲轩开启Polymath计划，将上限降低到246。

 

而仅仅 六个月 以后，Maynard也发表了一篇论文， 独立研究 出比张益唐更强的算法，上限降为600，而且不仅适用于素数对，也适用于三元组、四元组等。

 

总之，这群数学家在质数上的造诣很深，也一直在想办法证明各种质数相关的猜想。

 

Lichtman四年来一直在研究质数，研究方向也始终围绕着本原集猜想和其他质数问题。

 

直到今年2月的某一天，26岁的Lichtman突然跟导师Maynard说，我 完全证明 本原集猜想了！

 

Maynard则表示：我 完全震惊 （complete shock）了！

 

论文链接：https://arxiv.org/abs/2202.02384

 

34年前的猜想

 

上世纪三十年代，匈牙利数学家Paul Erdős（厄多斯）提出本原集（primitive set）的概念，指的是一个整数集合，其中每个数字都大于1，且不可相互整除。

 

因为所有的质数不能互相整除，所以质数集合相当于本原集的一个特例。

 

 

当时本原集的作用仅限于证明一类特定的数字，也称为完全数、完美数（perfect numbers）。

 

尽管本原集的定义很简单，但其在数学界却很有价值。

 

比如，一个集合包含从501-1000的所有整数，因为互相都不能整除，所以它也是一个本原集，通过这种方式就能获得大量的本原集。

 

数学家后来为本原集定义了多个大小（size）的概念，而不是只是简单地查一下集合里的元素个数，其中一个称之为Erdős sum，即把集合中的每个数字n，将其代入表达式1/(n log n)，然后将所有结果相加即可。

 

 

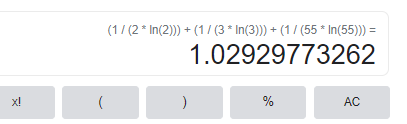
集合{2, 3, 55}的大小可以通过1/(2 log 2) + 1/(3 log 3) + 1/(55 log 55)计算得到。

 

1935年，厄多斯证明，对于任何本原集，哪怕是无限大的集合，这个Erdős sum的值总是有一个上限的。

 

虽然这个求和公式「至少在表面上看是完全陌生且模糊的」，但它在某些方面减轻了本原集的混乱程度，能否正确使用这个公式也成为是否会使用本原集的标准。

 

一个很自然的问题就来了：本原集最大的Erdős sum值为多少？

 

1988年，厄多斯猜想，质数集合有最大的Erdős sum，结果为1.64

 

几十年来，数学家绞尽脑汁在证明上下功夫，但也只能在特定类型的本原集上有效。

 

2019年，他和达特茅斯学院的导师Carl Pomerance发现本原集的Erdős sum不能大于1.78，仅比素数猜想的值大10%左右。

 

Lichtman和Pomerance通过将一个新的倍数序列与给定本原集中的每个数字相关联来获得这个常数。

 

比如在本原集{2, 3, 55}中，与数字2相关联的是所有偶数的序列。与数字3相关联的将是不是2的倍数的所有3的倍数，与数字55（5 × 11）相关联的将是所有55的倍数，因此乘数的最小素因数为11（不包括可被 2、3、5 和 7 整除的所有乘数）。

 

Lichtman将其比作单词在字典中的索引方式，仅使用素数而不是字母来组织每个序列。

 

 

然后，他和Pomerance思考了这些倍数序列有多「密集」，也就是说，它们在数字轴占据了多少。

 

例如，所有偶数的序列的密度为1/2，因为偶数占所有数字的一半。

 

他们观察到，如果原来的集合是本原集，则其相关的倍数序列不会重叠，因此它们的组合密度最多为所有整数的密度。

 

这一观察是相关的，因为19世纪数学家Franz Mertens的定理基本上允许Lichtman和Pomerance根据这些密度重新解释本原集的Erdős sum。

 

根据 Mertens 定理，一个特殊的常数（大约等于1.78），当乘以一个相当于这些倍数的组合密度的项时，给出了一个本原集的Erdős sum的最大值。并且由于组合密度最多为1，Lichtman和Pomerance证明了本原集的Erdős和最多为1.78左右。

 

James Maynard表示，这是Erdős最初想法的一种变体，但它是一种非常巧妙、简洁的方法，可以获得一个不严格但也不算太差的上限。

 

几年来，这似乎是数学家可以做到最好的结果了，目前尚不清楚如何将该最大值降至1.64。

 

在Lichtman毕业后到牛津大学与Maynard一起攻读博士学位时，Lichtman首先意识到，对于素因数相对较小的数字，他先前与 Pomerance 的论点仍然有效：相对简单地表明，在这种情况下，常数1.78可以被压低到远低于1.64。

 

但是具有相对较大素因数的数字，在某种意义上「接近」素数，是另一回事。

 

 

为了解决这些问题，Lichtman找到了一种方法，不仅可以将一个倍数序列与每个数字相关联，还可以将多个序列关联起来。和以前一样，所有这些序列的组合密度最多为1。

 

但这一次，这些其他倍数会像杂草一样生长并占据一些空间。

 

对于数字618（2 × 3 × 103）来说，通常，您可以将所有618的倍数与它相关联，这样乘数的最小素因数是103。但是可以使用一些被省略的较小素数来构建序列。

 

例如，一个序列可能由所有原始倍数组成，同时也允许618的倍数，其中乘数可以被5整除，一些限制规定可以使用哪些较小的素因数。

 

这些额外倍数的存在意味着原始倍数的组合密度，即Mertens定理中使用的数量，实际上小于1。Lichtman找到了一种方法来更精确地确定该密度可能是多少。

 

然后，他仔细确定了本原集的最坏情况可能是什么样的：它将在具有大素因数的数字和具有小素因数的数字之间取得什么平衡。通过将他的证明的两个部分拼凑在一起，他能够证明这种情况下的Erdős和的值小于1.64。

 

今年2月，Lichtman在网上发布了他的证明。数学家指出，这项工作特别引人注目，因为它完全依赖于基本论证，这些想法非常聪明。

 

Maynard表示，这是获得该数值的关键时刻，我不知道是运气还是什么，但这在数字上已经足够了。

 

这些想法巩固了素数在本原集中的特殊性，与Erdős sum一样处于顶端地位。

参考资料：

https://www.quantamagazine.org/graduate-students-side-project-proves-prime-number-conjecture-20220606/