【GNN】R-GCN：GCN 在知识图谱中的应用

今天学习的是阿姆斯特丹大学 Michael Schlichtkrull 大佬和 Thomas N. Kipf 大佬于 2017 年合作的一篇论文《Modeling Relational Data with Graph Convolutional Networks》，目前引用超 400 次，虽然这篇文章只是发到了 C 类会议，但论文中提出的 R-GCN 无疑开创了使用 GCN 框架去建模关系网络的先河。(只发到 C 可能是因为 R-GCN 表现不太好)

这篇论文主要有两大贡献：

1. 证明了 GCN 可以应用于关系网络中，特别是链接预测和实体分类中；
2. 引入权值共享和系数约束的方法使得 R-GCN 可以应用于关系众多的网络中。

Introduction

存储知识的知识库常用于多种应用，包括问答、信息检索等。但即使是最大的知识库（如Yago、Wiki等）也存在很多缺失信息，这种不完整性会影响到下游应用。而预测知识库中的缺失信息是统计关系学习（statistical relational learning，以下简称 SRL）的主要内容。

假设知识库主要以三元组的形式（主语、谓语、宾语）进行存储。比如说，Mikhail 在 Vaganova 学院上学，我们把 Mikhail 和 Vaganova 学院称为实体，受教育称为关系，每个实体会有自己的类型，这样便构成一张知识网络：

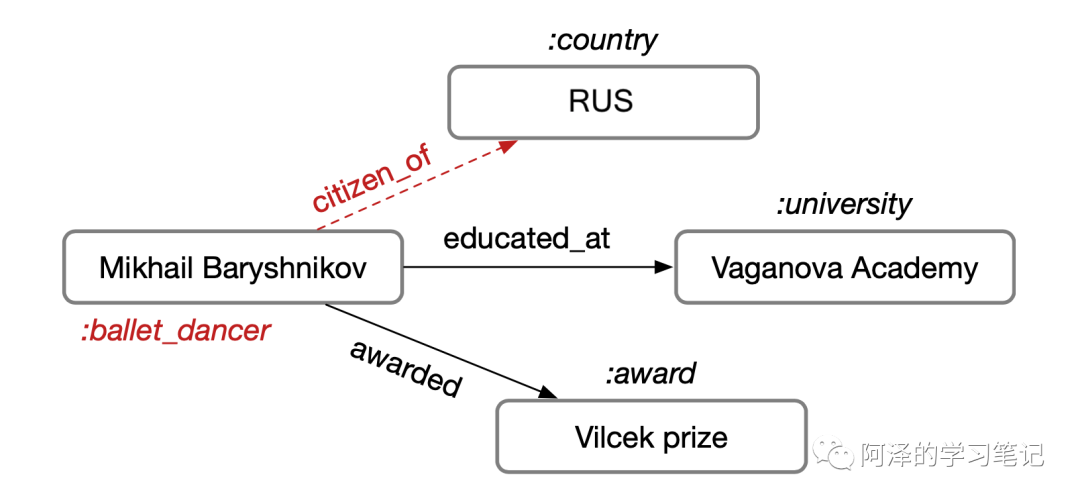
这篇论文主要考虑两个任务，包括「链接预测」和「实体分类」。在这种情况下，可以对很多缺失信息进行补全，比如说：知道 Mikhail 在 Vaganova 学院受过教育，我们便可以知道他居住在俄罗斯（RUS），并且有自己的 label （如图中红色部分）。

根据这种想法，作者设计了一个编码器模型，并将其应用于这两个任务中，简单来说：

• 对于实体分类来说，将在编码器后面接一个 softmax 分类器用于预测节点的标签；
• 对于链路预测来说，可以后面接一个解码器，将分类器视为自编码器，从而完成节点的预测。

R-GCN

RGCN

首先，目前的 GCN 可以视为一个简单可微的消息传递框架的特殊情况：

其中， 表示隐藏层 l 的节点 ； 表示消息传入； 表示激活函数。

写的具体一点的话 就是那个经典的 GCN。基于这个模型作者定了一个简单的前向传播模型：

其中， 表示节点 i 在关系 r 下的邻居节点的集合； 是一个标准化常量，可以实现指定也可以学习得到。

从上面这个公式中我们可以得到以下几点信息：

• R-GCN 的每层节点特征都是由上一层节点特征和节点的关系（边）得到；
• R-GCN 对节点的邻居节点特征和自身特征进行加权求和得到新的特征；
• R-GCN 为了保留节点自身的信息，会考虑自环。

与 GCN 不同的地方在于 R-GCN 会考虑「边的类型和方向」。

在实践中，利用稀疏矩阵乘法可以有效地实现前向传播，同时为了避免了对邻域的显式求和，可以将多层堆叠起来，以便跨多个关系步骤实现依赖关系。

R-GCN 模型中单节点更新的计算图如图下所示，其中红色节点为将被更新的节点，蓝色节点为邻居节点：

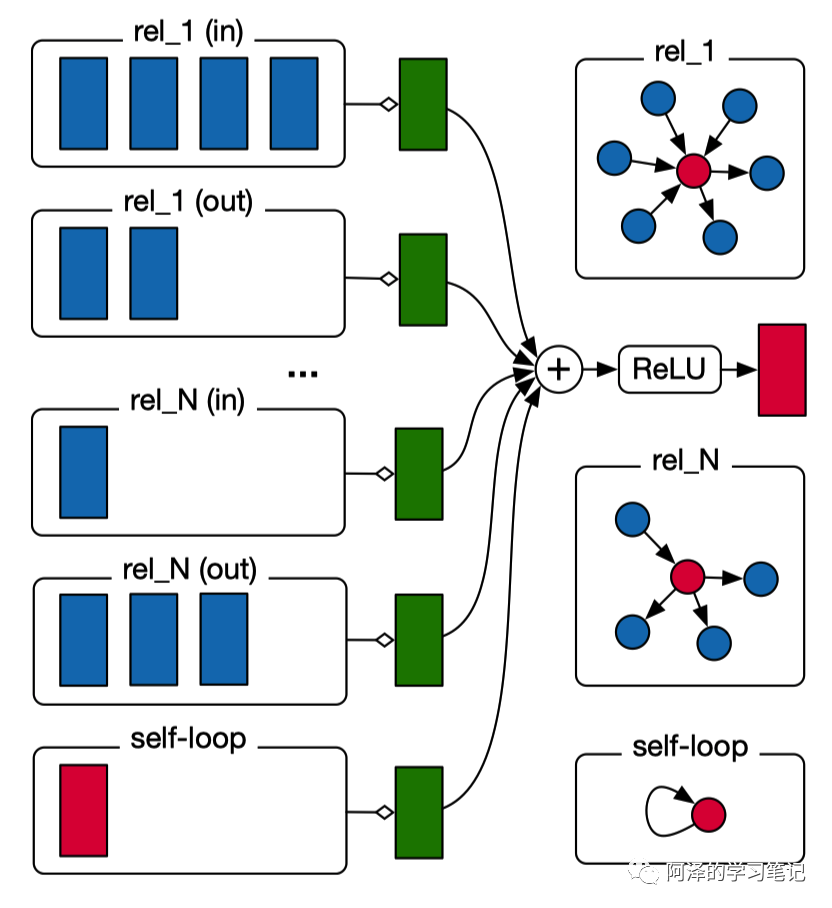
Regularization

为了出现过拟合的问题，作者考虑了两种正则化方法：

一种是「基函数分解」（basis decomposition）

其实也就是 和系数 的线形组合。

另一种是「块分解」（block diagonal decomposition）

为一块对角矩阵， 。

基函数分解可以看作是不同关系类型之间权重共享的一种方式；而块分解可以看作是对每个关系类型的权值矩阵的稀疏约束，其核心在于潜在的特征可以被分解成一组变量，这些变量在组内的耦合比在组间的耦合更紧密。

两种分解都减少了网络的参数数量。同时，参数化也可以缓解对稀有关系的过度拟合，因为稀有关系和常见关系之间共享参数更新。

Entity Classification

对于实体分类来说，只使用了堆叠的 R-GCN 并在最后一层叠加了一个 Softmax 层用于分类，并考虑交叉熵损失函数：

其中，y 为有标签的节点的集合； 表示输出层有标签的第 i 个节点的第 k 个实体的预测值； 表示节点本身的标签。

实体分类的架构如下图所示：

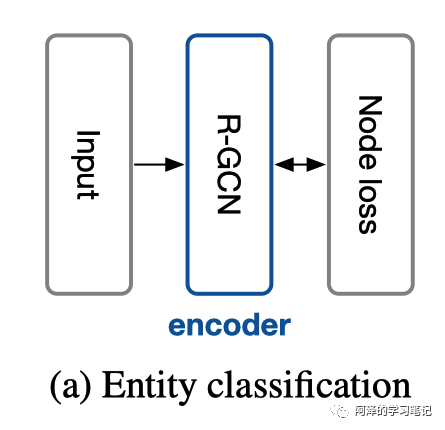
Link Prediction

知识库通常是一个有向有标签的图 ，V 表示节点，E 表示边，R 为关系。通常 E 是不完整，我们的目标就是预测缺失的边。

链接预测其实是预测一个三元组（subject，relation，object），作者通过一个打分函数 来判断 是否符合要求。

作者考虑使用 DistMult 分解作为评分函数，每个关系 r 都和一个对角矩阵有关：

考虑负采样的训练方式：对于观测样本，考虑 个负样本，并利用交叉熵损失进行优化：

链接预测模型的架构图如下所示：

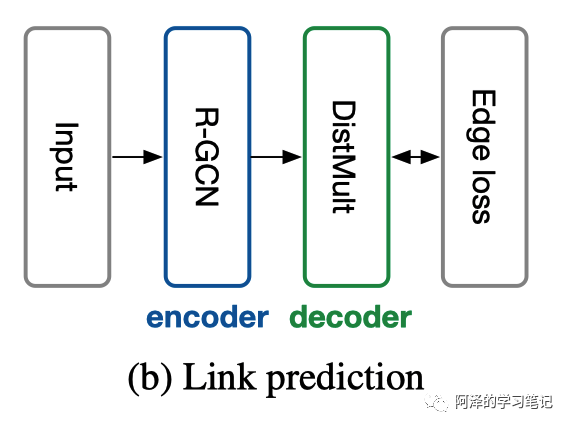
Experiments

简单看一下实验。

首先是实体分类的准确性：

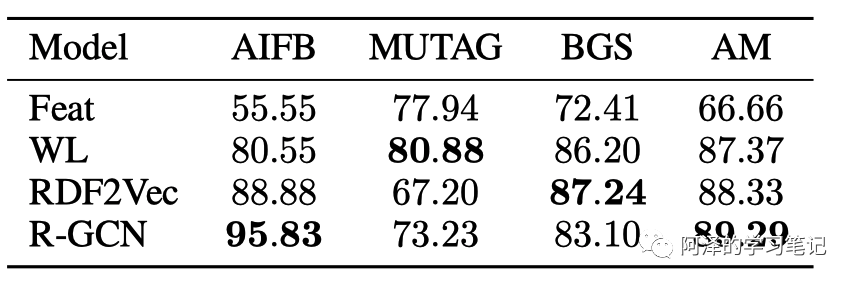
其次是链接预测的准确性：

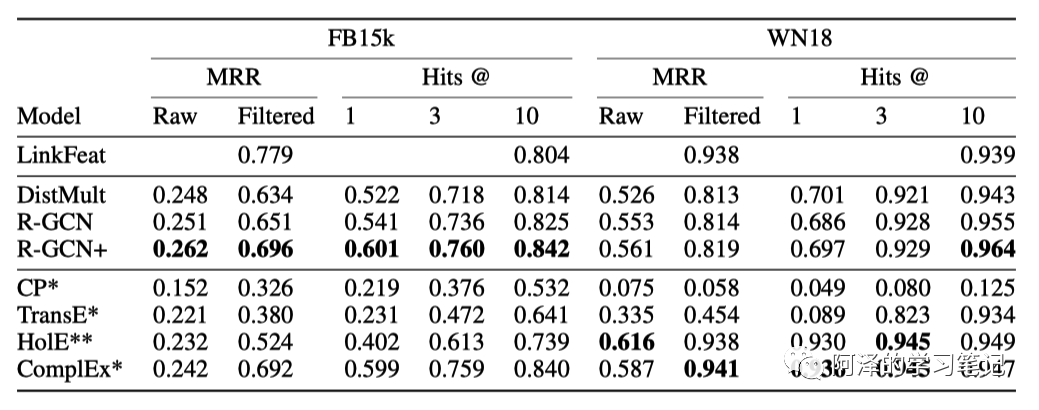
在数据集 FB15k-237 数据集上的表现：

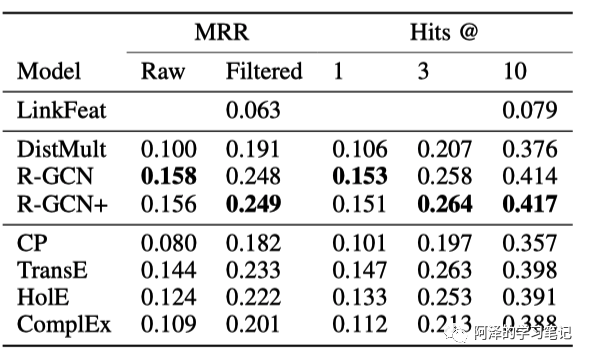
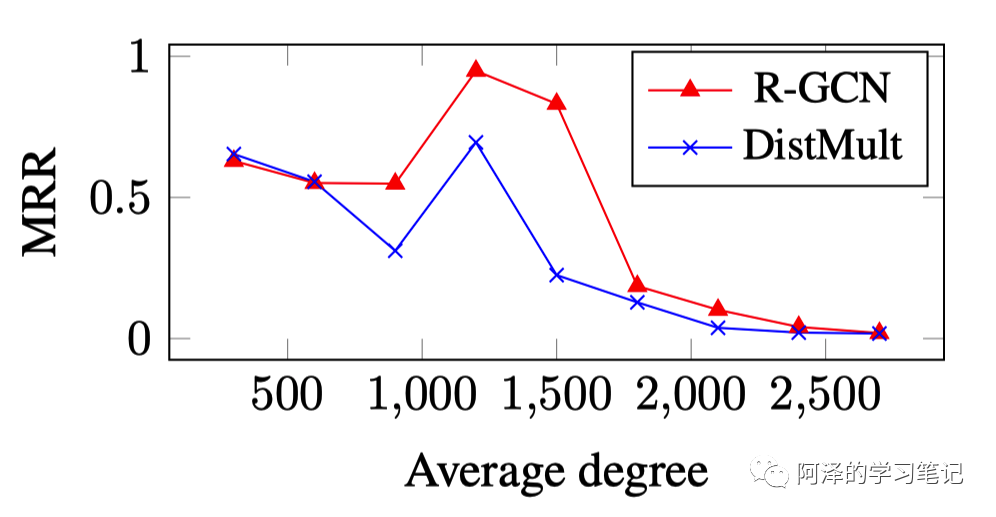
考虑 MRR 评分标准，不同度下的模型表现：

Conclusion

总结：R-GCN 构建了一个编码器，并通过接入不同的层完成不同的建模问题，如接入 Softmax 层进行实体分类，接入解码器进行链接预测，并在相应数据集中取得了不错的成绩。

Reference

1. 《Modeling Relational Data with Graph Convolutional Networks》
2. 《Github: relational-gcn》
3. 《eswc2018_kipf_convolutional_networks》

---

投稿或交流学习，备注： 昵称-学校（公司）-方向，进入DL&NLP交流群。

方向有很多： 机器学习、深度学习，python，情感分析、意见挖掘、句法分析、机器翻译、人机对话、知识图谱、语音识别等。

记得备注呦

让更多的人知道你“在看”