利用RNN训练Seq2Seq已经成为过去，CNN才是未来？

2017 年 10 月 31 日 AI100 大家都在关注

翻译 | AI科技大本营（rgznai100）

参与 | Shawn、周翔

当前 seq2seq （序列到序列）学习惯用的方法是，借助 RNN（循环神经网络）将输入序列转变为变长输出序列（variable length output sequence），而 FAIR （Facebook AI Research）则提出了一种完全基于 CNN （卷积神经网络）的架构。相比循环模型，其训练过程中所有元素的计算都可以完全并行化，GPU 硬件的性能可以得到更好的利用；而且，由于非线性的数量是固定的并且不受输入长度支配，优化起来也更加容易。

FAIR 使用门控线性单元（gated linear units，GLU）缓和了梯度传播，还在每个解码器层上都装了一个独立的注意力（attention）模块。在机器翻译比赛 WMT'14 中，FAIR 的架构的“英语-德语”和“英语-法语”翻译的准确度超过了 Wu 等人（2016）的深度 LSTM 架构，而且在 GPU 和 CPU 上的运行速度也有数量级的提升。

AI科技大本营对论文进行了简要翻译，想要查看完整论文，请点击文末“阅读原文”

1. 引言

使用 Seq2Seq 学习在很多任务中已经有成功的应用，例如机器翻译、语音识别和文本摘要等。目前最常用的方法是使用一系列的双向 RNN 对输入序列进行编码，再用一系列的解码器 RNNs 生成一个变长输出序列，输入和输出序列通过一种软注意力（soft-attention）机制联系在一起。试验证明，在机器翻译任务中，这个架构的表现要比传统的基于短语（phrase-based）的模型好得多。

尽管 CNN 独具优势，用它来进行序列建模却不是很常见。相比循环层，卷积层可以生成的是固定大小的上下文的表征，但是，只要在彼此顶部叠加几层卷积层，就可以增加网络的有效上下文大小。这样就可以准确控制要建模的依赖关系的最大长度。卷积网络不依赖于对上一时步（time step）的计算，因此序列中每个元素的计算都可以平行化，而 RNN 则必须维持先前所有时间步长的隐藏状态，这阻止了序列内的平行计算。

多层卷积神经网络生成层级式表征，较近的输入元素在较低的层相互作用，而较远的元素则在较高的层相互作用。相比循环网络建模的链结构，层级式结构提供了一种较短的路径来捕获词之间远程的依赖关系，例如获取一个可以捕捉 n 个单词（一个窗口）之间关系的特征表达，卷积核（kernel）宽度为 k 的卷积网络只需进行 O(n/k) 次卷积操作，相比之下，循环神经网络则需进行 O(n) 次操作。在输入数据时，卷积网络进行恒定次数的卷积核操作和非线性计算，而循环网络则是对第一个单词进行 n 次操作和非线性计算，对最后一个单词只进行单次操作集合。此外，固定对输入进行非线性计算的次数也可以简化学习过程。

在最近的一些研究中，卷积神经网络已被用于进行序列建模，如 Bradbury 等人的研究（2016）提出在一连串卷积层之间进行循环 pooling；Kalchbrenner 等人的研究（2016）尝试不借助注意力机制处理神经网络翻译任务。但是这些方法在大型基准数据集上的成绩都没有超过当前最优成绩。Meng 等人在 2015 年曾探讨过利用 Gated convolutions 完成机器翻译任务，但是他们评估的对象只限于一个小数据集，而且用的还是一种与传统的基于计数的模型协作的模型。这种部分卷积的架构在处理较大的任务时表现优异，但是他们的解码器仍然是循环网络（Gehring 等人, 2016）。

在本文中，我们提出了一种用于 Seq2Seq 建模任务的纯卷积架构。我们的模型配有门控线性单元和残差连接（residual connections）。我们还在每个解码器层使用了注意力机制，每个注意力层只添加数量足以忽略不计的 overhead。借助以上组合，我们可以处理大型任务。

我们在几个大数据集上对用这种方法完成机器翻译和文本摘要任务进行了评估，并将评估结果与当前的最佳架构进行了比较。在 WMT’16 的“英语—罗马尼亚语”翻译中，我们以 1.9 BLEU 的优势超越了先前的最佳成绩。在 WMT’14 的“英语—德语”翻译中，我们以 0.5 BLEU 的优势超越了 Wu 等人（2016）提出的 LSTM 系统。在 WMT’14 的“英语—法语”翻译中，我们以 1.6 BLEU 的优势超越了Wu 等人（2016）提出的概率训练系统（likelihood trained system）。另外在即时翻译语句时，我们的模型在 GPU 和 CPU 硬件上的运行速度要比 Wu 等人提出的系统（2016）要快一个数量级。

2. 循环序列到序列学习

序列到序列建模已成为基于循环神经网络的编码器—解码器结构(Sutskever 等人, 2014; Bahdanau 等人, 2014)的同义词。编码器 RNN 处理元素数量为 m 的输入序列 x = (x1, . . . , xm)，返回状态表征 z = (z1. . . . , zm)。解码器 RNN 代入 z，然后从左到右生成输入序列 y = (y1, . . . , yn)，每次生成一个元素。在生成第 y(i+1) 个输出元素时，解码器根据先前的状态 hi 计算出一个新的隐藏状态 h(i+1)，一个先前目标语言单词 yi 的内嵌 gi，以及从解码器输出 z 中提取出的一个条件输入 ci。基于这种方式，学界提出了很多种不同的编码器—解码器架构，这些架构的不同之处主要在于条件输入和 RNN 类型的不同。

未使用注意力机制的模型只考虑最终编码器的状态 zm，方法是对所有 i 进行 ci = zm 的设置；或者用 zm 初始化第一个解码器的状态，不使用 ci。使用注意力机制的架构在每个时步（time step）将 ci 计算为 (z1. . . . , zm) 的一个加权总和。总和的权重被称为注意力分数（attention scores），它可以使网络在生成输出序列时考虑输入序列的不同组成部分。计算注意力分数，根本上就是将每个编码器状态 zj 和先前解码器状态 hi 和最终预测 yi 的组合进行比较；计算结果进行正则化，最终形式为在输入元素上的分布。

编码器—解码器模型中的循环网络常为长短期记忆网络以及门控循环单元。这两种网络都是通过一个门控机制对 Elman RNNs 进行的延伸。门控机制可以使网络能记忆先前时步（time step）中的信息，对长期依赖（long-term dependencies）进行建模。最近提出的方法也是依靠双向编码器来为先前的上下文和之后的上下文构建表征。层数很多的模型通常依赖于 shortcut 连接或 residual 连接。

3. 卷积架构

接下来，我们提出了一个处理序列到序列建模任务的纯卷积架构。我们使用 CNN 来计算中间编码器状态 z 和解码器状态 h，而不是使用 RNN。

3.1 位置嵌入（Position Embeddings）

首先，我们在分布式空间中嵌入输入元素 x = (x1, . . . , xm)，并将其表示为 w = (w1, . . . ,wm)，其中

是嵌入矩阵

中的一列。我们还嵌入了输入元素 (p1, . . . , pm) 的绝对位置，其中

这样，我们就可以得出输入元素表征 e = (w1 + p1, . . . ,wm + pm)。我们对解码器网络生成的输出元素进行类似的操作，将得出的输出元素表征输入到解码器网络 g = (g1, . . . , gn) 中。位置嵌入在我们的架构是很有用的，因为它可以使我们的模型感知到现在处理的是输入序列或输出序列的哪一部分。

3.2 卷积块架构（Convolutional Block Structure）

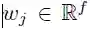
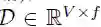
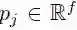
编码器网络和解码器网络用的都是同一种块结构，这种结构根据恒定数量的输入元素来计算中间状态。我们将解码器网络的第 l 个块结构的输出表示为 hl= (hl1, . . . , hln)，将编码器的第 l 个卷积的输出表示为 Zl= (Zl1, . . . , Zlm)；本文中的“卷积块”和“卷积层”可以互换。每个卷积块都包含一个后跟一个非线性的一维卷积。对于只有一个卷积块且卷积核宽度为 k 的解码器网络，每个输出状态 hil 都包含 k 个输入元素的信息。在每个卷积块顶部叠加几个卷积块，这样就可以增加每个状态代表的输入元素的数量。例如，设定 k = 5，叠加 6 个卷积块，那么我们可以得到一个由 25 个元素组成的输入字段（input field），即每个输出依赖于 25 个输入。非线性可以使网络利用整个输入字段，或者在需要时只用考虑更少的元素。

每个卷积核都参数化为

和

，

并作为输入

，

它是嵌入在 d 个维度中的由 k 个输入元素组成的一个字符串。这些元素被映射至一个输出元素

，

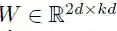
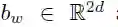
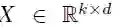
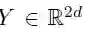
这个输出元素的维数是输入元素维数的两倍；后面的卷积层处理前面卷积层的 k 个输出元素。我们选择门控线性单元作为非线性，用它对卷积的输出执行一个简单的门控机制

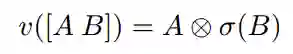
Oord 等人的研究中也提出了类似的非线性，他们对 A 进行了 tanh 计算，但是 Dauphin 等人的研究表明 GLU 在语言建模任务中的表现更好。

为了构建深度卷积网络，我们将每个卷积的输入的 residual connections 添加到卷积块的输出中。

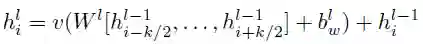
在编码器网络中，我们在每个卷积层填充输入，确保卷积层的输出与输入长度相匹配。但是，在解码器网络中，我们必须确保解码器没有更多信息。

我们还在大小为 f 的嵌入和大小为 2d 的卷积输出之间的映射中添加了线性映射。最后，我们计算了 T 个可能的下一目标元素 yi+1 的分布：

3.3 多步注意力（Multi-step Attention）

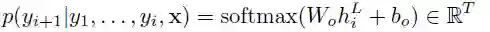
我们提出了一种在每个解码器层上应用的独立注意力机制。为了计算该注意力机制，我们将当前的解码器状态 h 与先前的目标元素 g 合并在一起：

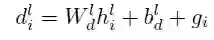
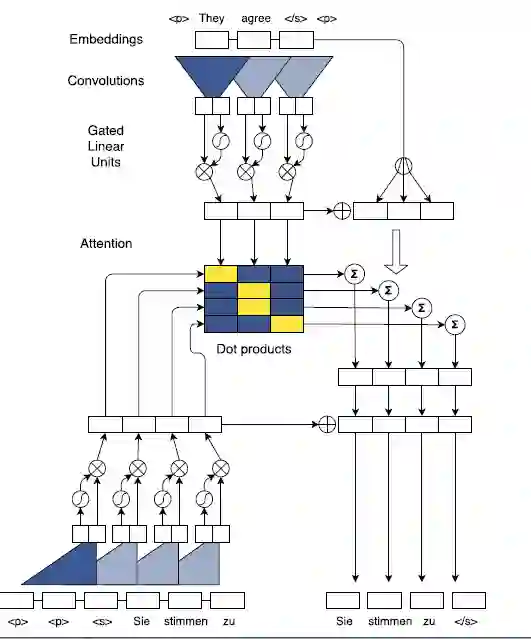
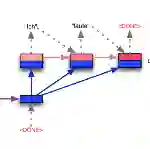
图1. 训练过程中的 batching 示图。我们对英语源语句进行了编码（顶部），并同时计算了四个德语目标单词（中部）的所有Attention值。我们的Attention正是解码器上下文标准（底部左侧）和编码器表征之间的点积。我们将Attention（中部右侧）计算的条件输入加到解码器状态中，预测目标单词（底部右侧）。S形框和乘法运算框表示的是门控线性单元。

对于解码器层 L，状态i 的Attention alij和源元素 j 计算为解码器状态摘要 dli 和最后一个编码器卷积块 u 的每个输出 zu 之间的点积。

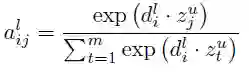
当前解码器层的条件输入 c 是编码器输出以及输入元素嵌入 e （图1，右侧中部）加权总和：

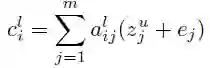
总的来说，我们的注意力机制可以考虑之前注意到哪些单词，并在每个时步上执行多个注意力‘hops’。

与 RNN 相比，我们的卷积架构还允许将序列的所有元素的注意力计算（图1，中间）进行批处理，我们分别对每个解码器层的计算进行批处理。

3.4 归一化策略（Normalization Strategy）

我们谨慎地对权重进行了初始化，以稳定学习过程，同时我们还对网络的各部分进行了 scale 操作，以确保网络的 variance 不会发生较大的变化。特别地，我们缩放了残差（residual）卷积层的输出以及Attention，以维持激活函数的 variance。我们将输入和一个残差卷积块的输出的总和乘以√0.5 ，以将总和的 variance 减少一半。假设被加数有相同的 variance，该假设不一定正确，但是在实践中却有效。

3.5 初始化（Initialization）

在加入不同层的输出时，如 residual connections，正则化激活需要进行谨慎的权重初始化。初始化的目的与正则化的目的相同：在整个前向和后向传递过程中维持激活函数的偏差。均值为 0、标准差为 0.1 的正态分布的所有嵌入都经过初始化。对于输出不直接转递到门控线性单元的层，我们从

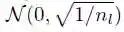
开始对权重进行初始化，其中 n 是每个神经元的输入连接的数量，这样可以确保正态分布的输入的 variance 保持不变。

对于正好在 GLU 激活之前的层，通过调整（He et al., 2015b; Glorot & Bengio, 2010）中的衍生方法，我们提出了一种权重初始化方法。如果 GLU 输入的分布函数均值为 0，并且 variance 足够小，我们就可以使用输入 variance 的四分之一近似估计输出 variance。因此，我们对权重进行了初始化，这样 GLU 激活函数的输入偏差就是输入层偏差的4倍。实现方法是从

中提出初始值。当构建好网络后，将 variance 全部设为 0。

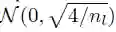
我们在一些层的输入中执行了 dropout，这样输入的概率值就始终为 p。这还可以看作为乘以一个 Bernoulli 随机变量，代入概率 p 计算 1/p 值，不涵盖 p为 0 的情况。Dorpout 的应用可以使偏差缩放 1/p 倍。我们的目的是使用较大的权重初始化各层，以恢复输入的偏差。具体的做法是，对输出由 GLU 处理的层使用

，

对于其他层，则使用

结论

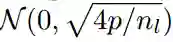
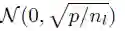
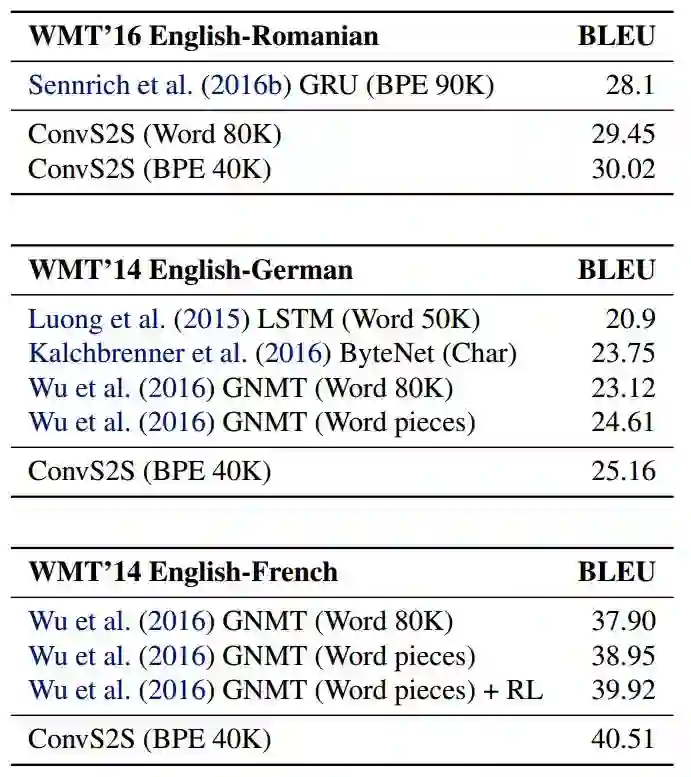
表1：与以前的工作相比，我们的模型在WMT任务上的准确率。ConvS2S 和 GNMT 的结果是多次测试之后的平均值。

我们针对 Seq2Seq 第一次引入了全卷积模型，该算法在非常大的基准数据集上的表现，超过了 RNN。与 RNN 相比，我们使用的卷积方法更容易发现序列中的组成结构，因为表征实际上是分层构建的。我们的模型依赖于 gating（门控），并需要之执行多重 attention 步骤。

我们引入了序列学习的第一个完全卷积模型，该算法在非常大的基准数据集上以超过一个数量级的速度超越强反复模型。与循环网络相比，我们的卷积方法允许更容易地发现序列中的组成结构，因为表示是分层构建的。我们的模型依赖于门控，并执行多重注意的步骤。

我们在几个公开的翻译基准数据集上都取得了目前最好的成绩。在“WMT'16 英语 - 罗马尼亚语”的任务中，我们超出目前最佳成绩 1.9 BLEU。相比 Wu 2016 年的 LSTM 模型，在“WMT'14 英文 - 法文”翻译任务中，我们进步了 1.6 BLEU，而在“WMT'14 英语 - 德语”翻译任务中，我们进步了 0.5 BLEU。

在未来的工作中，我们希望将卷积架构应用到其他的 Seq2Seq 学习问题中去，而这些问题也很可能从学习分层表征中受益。