Cross-Modal & Metric Learning 跨模态检索专题-3(上)

2020 年 5 月 22 日 AINLP

·前言

专题链接：

本专题计划分3个部分共4篇文章介绍图文跨模态检索的一些工作与思考。第一篇将侧重 "multi-modal" 和 "application", 介绍相关概念与研究背景；第二、三篇会侧重"algorithm" 介绍这个方向研究的技术路线，其中第二篇介绍基于 GAN 的追求公共子空间的 cross-modal 检索；第三篇则从 modal 抽象成更一般的 domain，并且将多域扩展到单域，总结分析单/多域匹配问题，主要介绍基于 contrastive learning / instances discrimination的研究思路。

本篇内容删除了我工作中未公开的信息、也删改了与在投 paper 有关的内容，所以有些地方只能"点到为止"。虽然删减了很多，但是内容实在写的太多了，微信又不支持公式输入，为了提升速度满足同学催更，所以第3篇拆成上、下两篇发出。（早知道就用视频讲了）

本文脉络

(上篇)无监督表示学习与Instances discrimination
(上篇)问题的一般抽象
(上篇)采样的各种花式组合
(下篇)配合采样的各类 Loss 函数

—

无监督表示学习 & Instance discrimination

前两篇我们基于图、文这两种模态信号进行了一些介绍，所介绍的一些方法和思路都是通用的技术路线，并没有涉及模态信号本身的特性。本篇将"跨模态"（cross-modal）这个概念进一步泛化，首先引申到"跨域"（cross-domain），接着更进一步在"跨个体" instance 级别来进一步介绍基于模型 Loss 设计的这一类优化方法。

从跨模态到跨域是指，检索和被检索的两个信号，可能都是同一个模态的数据，比如都是图片、都是文字、或者同为语音等等，只不过这2个 domian 的样本可能是具有不同的人工定义，比如关键词到文章的检索，虽然都是文本信号，但是一个是较短的 query，一个是很长的 document。

"跨个体"并不是一个成文的叫法，我们还是用"instance discrimination"来代指这一类吧。这类方向研究的问题相当于是个体到个体的检索，举个并不恰当的例子：输入一个词"开心"，能够检索出"高兴"；给一张老虎头部的图片，能够知道这是代表老虎，是和另一张老虎尾巴的图片是一类的。总之 instance discrimination 可以认为是同域内的样本检索。

无监督表示学习一直是当前研究的热点，尤其从去年开始，何凯明的 MOCO 放出后，我们又看到了 Hinton的相关工作 SimCLR, 近期何凯明又推出了 MOCO2. 一下子把 contrastive learning 推到了一个新的热度。而这些工作所研究的问题就是我们这儿说的 instance discrimination。只不过他们是加了无监督这一限制。

按我个人的理解简单归纳了这类研究的本质，可以用3句话概括：

『我是谁？我和谁有关？关系如何？』

只要回答了这灵魂三问，就算是弄明白了 instance discrimination 研究的本质了。我们还是以检索系统为例，考虑一个简单的任务：输入一个 query 文本比如"惊喜"，然后召回最相关的 top 3的文本结果。那么我们首先得弄明白"什么叫惊喜"，即第一个问题『我是谁』。

知道了我（惊喜）是谁后，第二个问题是我和谁有关？就是说我们要知道有哪些词和惊喜有关。接着想要返回 top 3的结果，还要回答好第三个问题，即关系如何，怎样就能算是 top 3 ？

上面3个问题，不同场景下我们可以采用不同方法来解决，比如可以使用 HSV 、Gabor等特征（feature）来表示一个图片样本（instance）；也可以使用12345这样的 id 值来代表一首歌曲样本；可以用id 数字的差异位数来表示两个歌曲样本的关系...更一般的情况，我们会使用一个 embedding 向量来表示这个样本，然后利用向量间的距离或夹角来表示样本间的关系。这类研究所属的范畴可以是 metric learning、contrastive learning 等等。

上面那个"惊喜"的例子，是不是感觉好像很适合 word2vec ？没错，word2vec 就是很经典的 NLP 领域的无监督表示学习，能够根据样本 vector 的分布，描述这个样本的意义以及和周围哪些词类似。在图片任务中也一样，比如 imageNet 1K 的数据集，给一张猫的图片，首先得知道这是猫，然后要知道还有哪些图片也是猫，最后这些猫中，哪几个和给定的猫最相似。

NLP 中无监督的数据集是很容易得到的，比如百度百科、维基百科的所有词条可以作为中文/英文语料。在图像领域，无监督的数据，往往不是那么容易得到的。这个"往往"是指经典的分类、检测、分割这些任务，但是最近就分类任务而言，也逐渐的产生了一个无监督的潮流比如 MOCO 等。图片的无监督数据获得常用的有上图的几个方法：彩色图转灰度图（用于自动上色任务）、图片加噪声（可用于重建）、图片抠掉一些像素（可用于 inpainting）、随机crop 旋转翻折色彩变换等（可用于图片理解、分类）。这些方法不像 NLP 中的那么自然，大多数是根据实际的任务来选择的，一般而言 crop 这一类方法效果最好、能应用的范围也最广。

—

问题的一般抽象

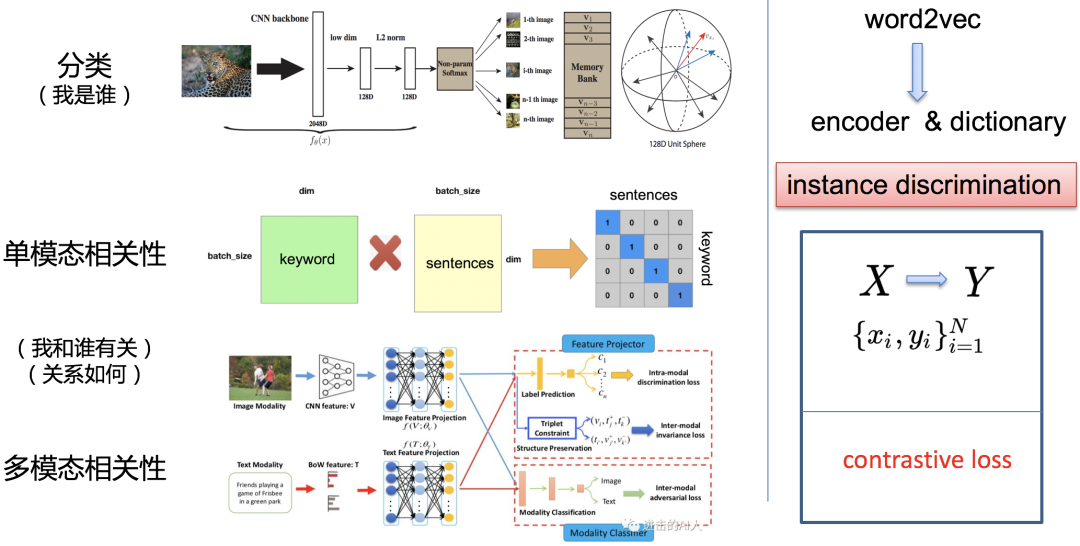
经过上面的介绍，我们已经知道了 instance discrimination 可以用于以下几类问题研究：1）单个样本信号的自我辩识（我是谁？如分类问题）；2）单个模态内部的样本间匹配检索，如用字数较少的 keyword 去检索出字数较多的段落 sentences；3）不同模态之间的检索召回问题。

近期的 instance discrimination 研究更多的是应用在第一类问题，因为大家都很热衷挑战无监督的这一限定。上面3类问题"本质上"都是一样的，我们可以从这些任务中，抽象出更一般的数学表达。还是以 word2vec 为例，instance discrimination 简单的说就是要找到一个编码器 encoder（通常用于连续信号或不可枚举信号）或者说一个词典 dictionary（比如离散输入的一个词语，类似一组基的集合可以是完备或者过完备的）来对我们要研究的信号进行编码后输出 embedding 向量。

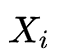
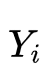
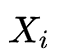
这类问题目前聚焦在用 contrastive learning 来解决。用数学表达就是，两个信号集合 X 和 Y（Y 也可以是 X 本身），给定 X 中一个，现在从 Y 中找到对应的则为正样本，和一起构成一个正样本 pair；其他不相关的 y 则属于负样本。我们通过这个规则，可以构造出N个样本组合。这些样本组合就是我们的训练数据。比如图片分类任务中，这个 Xi 可以是一张图片的一个 random crop，正样本Yi 可以是这张图片的另一个 crop，也可以是同类别的其他图片。其他类别不相关的图片及其变形则为负样本 y。

有了训练数据后，再构造一个 Loss 函数，拉近 Xi 和相关的Yi 正样本对之间（准确的说是X 和 Y经过网络后顶层的 embedding 之间）的度量距离，拉远不相关的负样本对的度量距离，这样一个contrastive learning 的框架就完成了。前面这个 loss 关注的度量距离，所以显然是为了解决"我和谁有关？关系如何？"这2个问题。如果只是一个"我是谁？"的任务， Loss 也可以直接对 embedding判断是哪一个类别，产生概率分布。

继续考虑，样本对只能是<X,Y>这样的的2元组吗？

很显然可以不是2元组，现在 metric learning 已经研究的很多了，关于如何构造样本 pair，以及上面说的度量距离如何设计等这些问题都有很多经典工作。我这里一会用 contrastive learning 一会又用 metric learning 目的就是让大家知道在本篇讨论的范畴内，这些都是指一个概念。

这类问题的核心套路就是，构造<X,Y>的样本组合采样，再定义一个距离如 cosine，然后配组合采样方式选择合适的 Loss 函数来更新模型。比如组合采样是 <X,Y> 2元组，Loss 则可以用 contrastive loss 或者cross entropy。组合采样是 <X,Y+,Y-> 这样的一个anchor 和一正一负的3元组，则 loss 可以用 triplet loss。组合采样是 <X,Y1,Y2,...,Yn> 的一正 N 负的结构，则 Loss 可以用 softmax。当然特定任务中还可以设计 N 正 M 负的组合，甚至也可以加入对 X 的组合比如 loss 里同时考虑同模态内部两个 X 样本的距离，这些非常重要，但是我们暂不讨论。

那么上面这些方式，那个效果更好呢？

一般任务而言，或者说理论而言，当我们对一个正样本采样到越多的负样本，模型效果会更好。关于这个理论其实就是互信息量 mutual information estimation，这个会在下面的小节中简单推导介绍。补充2点：1）不同任务，可能会存在不同的结论；2）模型效果好坏的标准，不能仅仅看 AUC，有的2元组 loss 天然有利于auc。

简单归纳下当前 contrastive learning 的核心就是研究下面2个问题：

从大家的研究方向来看，还是倾向于增加大量负样本采样，同时配合一些常规的类似无参softmax 或者negative log-likehood 函数当做 Loss 即可。下面就简单介绍下一些经典采样组合和 loss 设计。

—

采样的各种花式组合

上一小节已经提到了构造组合时可以有多种采样方式，本小节挑选经典的几个结构介绍下研究脉络。

最常用的采样组合就是上图这2种了，即二元组和三元组。二元组的数据通常都是提前组合好的，比如在图文相关性任务中，可以搜集一系列相关的图文二元组，和随机交叉的一系列不相关的图文二元组。而对于三元组这种采样组合，大多数场景还是输入的 <anchor,positive> 二元组当做训练数据，然后在一个 batch size 内寻找一个 negative 的样本来构成<anchor, pos,neg> 三元组。这种 batch 内构造 triplet pair 有多种方法，可以随机，可以挑选距离最近的等等，网上有很多成熟的开源代码。

这里提前补充下，二元组的方式由于可以提前构造负样本，所以这种情况下，可以很方便的实现 hard negative mining 和 fine-tuning，只要把额外的难分样本 pair 和需要微调的样本 pair 加入训练数据即可。而对于三元组组合，虽然也可以直接加到训练样本里（这是因为我们实际输入的就是二元组 pair），但是要清楚实际上我们在 batch 内部仅仅对<anchor,pos>进行了构造，而无法对<anchor, neg>构造3元组。无法直接在训练数据中增加指定的负例样本的问题，在下面的几个组合采样中会更明显。

上图中 contrastive embedding 和 tripet embedding 就是分别指二元组和三元组的组合方式。除此外，还有一个比较花哨的复杂组合(c) Lifted structured，这个采样组合里，同时考虑了跨域关系和同域内各样本关系。下一节会结合它的 loss 再介绍，这里我们知道组合可以多种多样就行，大胆的设计，只要有道理就可以，不要局限于跨域或者有限的pair。

lifted structured 的组合方式有点过于复杂，对训练数据要求也很高，因此很多场景下都不适用。目前大家研究的主流还是上图(d)这种在一个 batch-size 数据内部，对每一个输入正例 pair(a,b)，充分交叉组合，得到所有叉乘的负例组合，i.e. , <a1,b1>是正例输入那么交叉后<a1,b2>就是不相关的负例组合。这里的交叉可以是 cosine 距离，也可以是内积，内积的方式更简单，计算量和代码都容易一点。当然如果对 embedding 做归一化，那么 cosine 就等于内积。

我们可以看到 batch-wise 这种采样组合方式的目的是获得更多的负样本组合。那么也就是说，batch-size 越大，模型效果越好，是这样吗？还有，如果负样本组合越多，效果越好，是不是可以更大胆一点，做一个 beyond batch 的采样，把其他历史的 batch 内数据也拿到本次 batch 中进行交叉组合？

这里就有2个问题：A）是不是负样本越多越好？B）如果是，怎么构造出更多的负样本组合？

问题A其实上一个小节中已经给出答案了，从实际实验效果来看，一定范围内增大batch-size 可以提升效果，通过 beyond batch 的方式获得更多负例，也会提升效果。下一小节，在介绍对应的 Loss 函数时，我们再从互信息量的角度去给出数学推导。本小节我们先看下怎么获得更多的负例组合。

像上图(d)中在一个 batch 内部，将所有 pair 充分交叉可以获得大量的负样本，这种方式只使用了一个 batch 内的数据，无法运用其他 batch 的数据。因此想要增加负样本数，就只能增大 batch-size，但是随着 batch-size 的增大，会带来2个问题，一个是 GPU 显存不够，一个是超大 batch-size 优化问题（太大时很难训练优化）。我们称这种方式为end-to-end 的模式，因为这样每次梯度更新的时候都会把对应batch 内的 embedding都更新一下，如下图(a)所示。

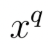
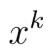
上图中的和，就是我们输入的一个 pair，即<X,Y>,分别通过编码器 encoder 后（两个 encoder 可以是一样，也可以不一样）得到其表示学习的顶层 embedding：q, k. 再利用 q,k 计算一个 loss 来反向更新参数。上图(a)的模式就是代表着前文说的 batch-wise 采样，是通过反向传播对计算查询和键的表征进行端到端更新，所以很优雅，但是负样本还是不够，毕竟一个 batch 内数量是有限的。

于是在18年的 CVPR 中，Wu 等人提出了上图(b)这种采样模式，即使用一个 memory bank 机制。简单的说就是维护一个很大的池子，把历史的一些 batch 数据存下来，然后只有被采样到 K 才会更新。这个模式的好处是，极大的扩大负样本的空间，但是问题是这样存储的编码 k 都是过时的（不是每个K都更新），且来自不同时间的（被采样的批次不同，被更新的时间也就不同）。

最近凯明大神的 MoCo 问世后，引起了很大的关注。上图(c)这个模式就是 Moco（Momentum Contrast），这个模式则是通过基于动量更新的编码器对键进行动态编码，并维持键的队列。其实这个思路在强化学习里就有。再提一下MoCo中还有一个比较重要的点是 shuffle BN。

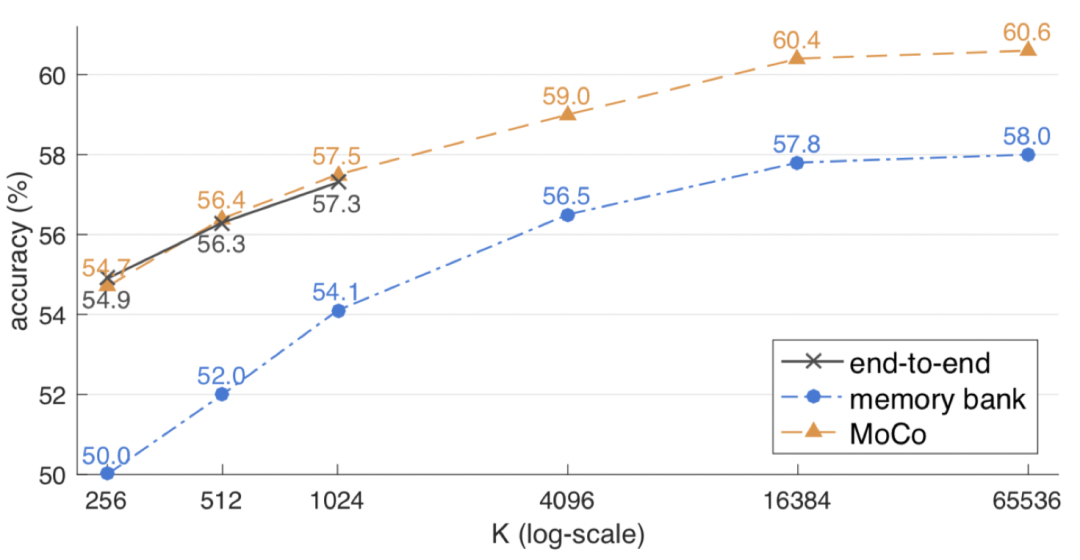
上面的 memory bank 和 MoCo 没有讲太多，感兴趣的同学可以读下 MoCo 的文章，比较清晰易懂的。我们这里只要了解到这种采样方式即可。看下实验的对比结果：

从上图实验比较来看，当负样本个数 K 较小时，一个 batch 能存下时，end-to-end 的效果和 MoCo 的差不多，都要远好于 memory bank。而随着 K 增大，MoCo 的效果也在逐渐变好，不过到65536左右，逐渐开始收敛了，提升空间不大了。这里个人理解是，当负样本多到一定程度，再增加负样本都是一些不重要的信息了，用 SVM 的定义来理解就是这时候，需要的是难分样本，再增加非边界样本，意义不大。这里又不得不提二元组的优势了，可以直接在样本中增加重要的负例。

前面提到的构造样本对时，以图片理解为例，正样本一般就是crop、mirror 等等常规的 data augmentation。这种方式得到的正样本变化还是不够充分，这里介绍一个最近看的工作，Watching the World Go By:Representation Learning from Unlabeled Videos，（https://arxiv.org/pdf/2003.07990.pdf）看视频理解世界。

简单的说就是把视频多帧信息利用起来，这样一个物体的多个视角都能当做 augmentation 了。同理，多了 time 这一维度，采样也可以再上升一个级别：

本小节介绍了各种采样组合，从原始的简单二元组，到最后复杂的视频版 NCE。大家需要了解脉络即可，同时也要辨别实际工作中哪个才是最合适的。可以明确的说，memory bank, MoCo, video-wise这些新模式大多数场景中没啥性价比可言。。。实际工作中，应该更多的重视 batch-wise 的采样方式。

—

配合采样的各类 Loss 函数

第3小节介绍了很多采样组合方式，本小节将介绍这些经典的采样可使用的 Loss 函数，同时会从互信息量的角度介绍为什么要增加负样本采样数量。

详见下篇~

推荐阅读

AINLP年度阅读收藏清单

薅当当羊毛的机会又！双！！叒！！！叕!!!来了

中文命名实体识别工具（NER）哪家强？

学自然语言处理，其实更应该学好英语

斯坦福大学NLP组Python深度学习自然语言处理工具Stanza试用

太赞了！Springer面向公众开放电子书籍，附65本数学、编程、机器学习、深度学习、数据挖掘、数据科学等书籍链接及打包下载

数学之美中盛赞的 Michael Collins 教授，他的NLP课程要不要收藏？

自动作诗机&藏头诗生成器：五言、七言、绝句、律诗全了

模型压缩实践系列之——bert-of-theseus，一个非常亲民的bert压缩方法

这门斯坦福大学自然语言处理经典入门课，我放到B站了

征稿启示 | 稿费+GPU算力+星球嘉宾一个都不少

关于AINLP

AINLP 是一个有趣有AI的自然语言处理社区，专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享，主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等，欢迎关注！加技术交流群请添加AINLPer(id：ainlper)，备注工作/研究方向+加群目的。