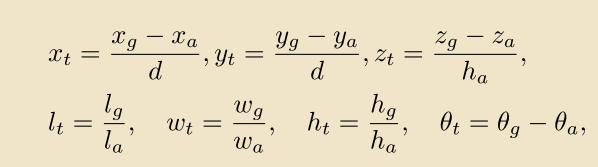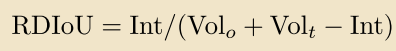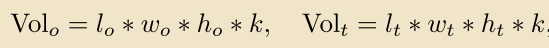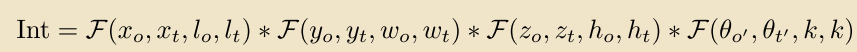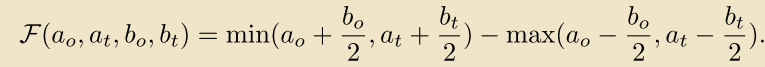论文题目
![]()
论文地址:
https://arxiv.org/abs/2207.09332
代码地址:
https://github.com/hlsheng1/RDIoU
提出问题
3D目标检测中,IoU依然是重要的性能评价标准。那么类似2D目标检测,3D IoU也能作为损失函数一致的训练和评估过程。作者认为3D IoU存在两个重要的问题:
-
-
旋转角度的引入会导致3D IoU优化的不稳定性和次优问题
问题分析
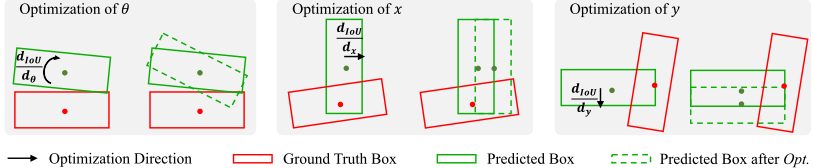
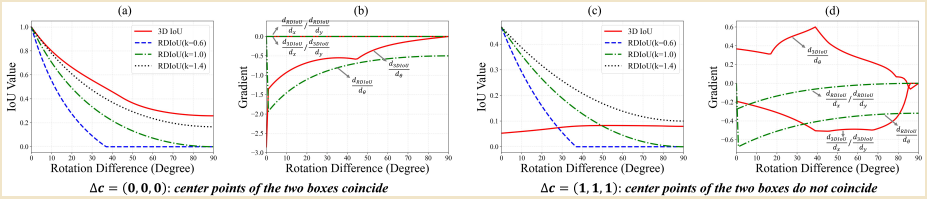
本文主要关注的是第二个问题,并做了细致讨论,作者认为:将旋转角与3D物体的中心点和形状进行耦合不利于3D IoU的优化。如下图所示:
最左边的图中,3D IoU loss会倾向于先旋转pbox来获得更大的IoU,但是这会导致角度预测偏移更大。中间和右边的图例分别展示了中心点的x和y预测过程中类似的情况。此外,3D IoU和2D的旋转IoU一样,都是不可微的。3D IoU的overlap也是采用三角分割的方法计算的,因而结果和两个bbox的相交点个数有关,在交点个数的变化边缘附近会出现梯度跳变。
提出方法
作者提出了一种旋转解码的Rotation-Decoupled IoU (RDIoU)来实现可微且训练与预测一致的结果。接着,将提出的RDIoU结合2D目标检测中的DIoU,GFIoU构造新的损失函数;最后,将提出的基于IoU的损失应用到不同的模型上取得性能提升,印证方法的有效性。本文重点在于DRIoU的构建方法,下面进行详细介绍。
相关定义
其中d是anchor在2D平面上的对角线长。ps: 实际上很多方法,包括作者的实现代码使用的并不是这种做法,而是类似2D通用检测的anchor offset encoding(参考Faster RCNN)。
RDIoU构建
作者为了解耦角度对IoU的影响,比较有趣地引入了第四维度地概念,将角度视作类似于3维bbox中长宽高之外的第四维度,然后重新计算四维空间的“IoU”。3D box表征由中心和形状组成,变成四维就是中心和形状。对于这个4D的表征,个人感觉可以理解成四维空间的的“水平包围框”,从而不难理解作者的IoU计算方式了。IoU表达式很简单:
其中,和分别为预测结果和GT的体积,从2D和3D的cases中不难归纳演绎出4D中的水平bbox的提及计算方法:
类似地,我们可以推导出两个4D box的交集公式:
这个也很好理解,类比2D HBBs之间的overlap计算方法就能得到。那么问题就落在怎么确定第四维度的和上。作者的做法是,直接取,而令。可以看到,出发点很有趣,落脚点其实相对简单的。但是这会带来一个直观问题:这个所谓的4D IoU不再能表征3D IoU,有可能导致损失和评估的不一致。作者通过下面的实验证明了提出的RDIoU的有效性:
图a展示了中心重合的情况下,不同值对RDIoU曲线的影响,通过调试能获得和3D IoU较为一致的性能评估结果。同时,时,RDIoU对旋转角度更加敏感,能获得更好的性能;图b可见此时的梯度变化较为一致,而且更加平滑可微。图c显示中心存在一定偏移的case,此时3D IoU并不能很好地敏感角度变化,而RDIoU反而有更好的效果;图d中显示,此时3D IoU甚至出现正梯度,导致角度优化更差,而RDIoU则能保持较好的优化性能。后面利用构造好的RDIoU,引进了DIoU,和GFIoU就没什么好说的,直接代换就行。
实验结果
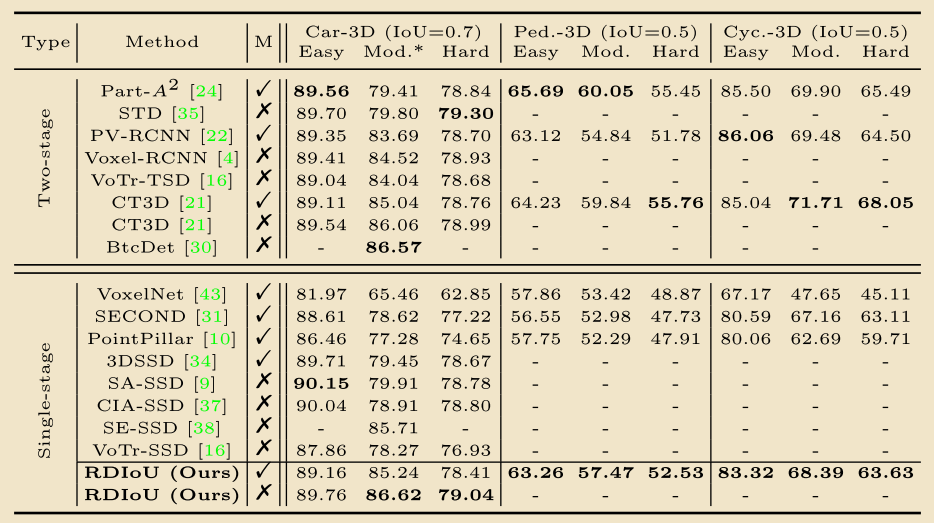
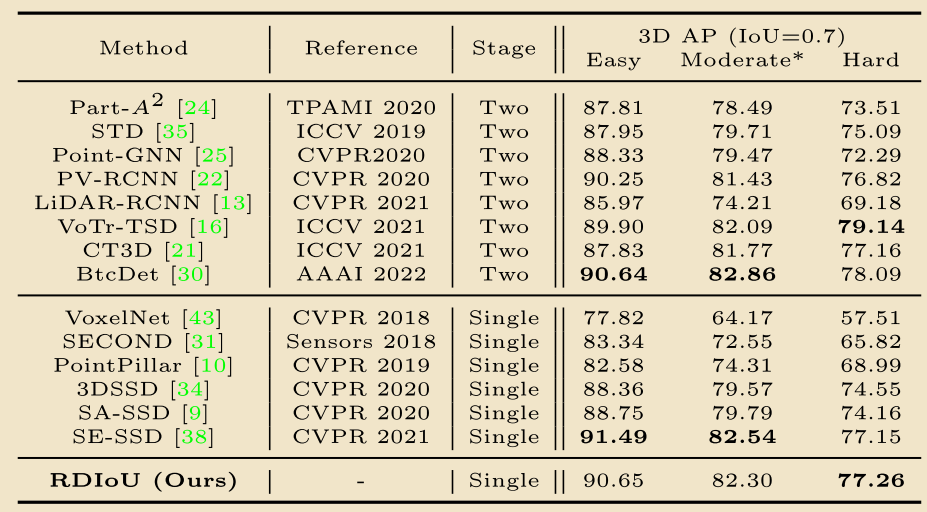
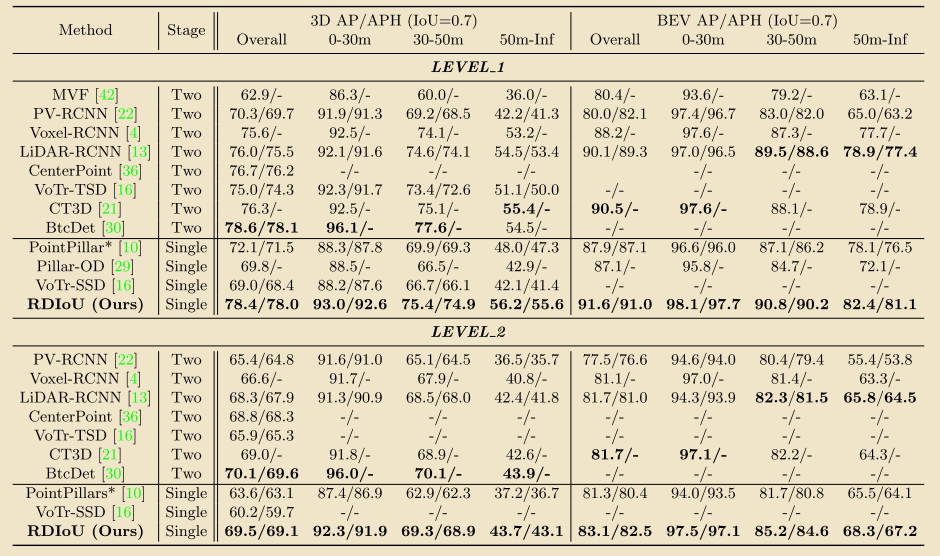
下面是一些直观的性能比较,可见RDIoU能实现更加快速收敛和高性能的检测精度。
还有一些ablations就不多说了,结果而言都是高于现有的IoU-based方法,例如DIoU,CIoU等。最后这里有几个问题还值得讨论:
-
公式来看,对RDIoU曲线的调节是非线性的,这个参数的优化值得进一步讨论
-
IoU损失的尺度不变性在RDIoU中能否得到体现?
-
定性实验只有两个特殊case,实际上对于旋转目标而言IoU敏感很多其他因素,考虑不够全面
-
3D IoU本身就是target,部分param暂时的偏移不当一定程度上是能够容忍的,RDIoU起作用的原因可能还有其他。
公众号后台回复“ECCV2022”获取论文分类资源下载~