温度计小史

今年的“三伏天”从7月17日开始，8月25日结束，炎炎夏日，大家更关心每天的温度。温度与我们日常生活的关系太密切了，上了年纪的人习惯关注每天《新闻联播》后的“天气预报”节目，年轻人更喜欢直接在手机上查看天气的动态信息，伴随天气变化的气温往往决定了未来几天的穿着或行程。自己或家人身体有些发热，自然会用体温计去测量。今天我们就聊聊有关温度计的故事，首先说温度计的发明，其次谈温标的确立，最后是温度计知识传入我国的过程。

一、 温度计的发明

大家或许想知道，在温度计发明之前，人类是如何表达温度高低的呢？很简单，靠经验描述。你可能还记得战国《列子汤问》中“两小儿辩日”的故事吧，一小儿为“近者热而远者凉”辩护道，“日初出沧沧凉凉，及其日中如探汤”。这便是很朴素的经验性描述。当然，古人还摸索出了稍微高级一点检测温度的办法，比如烧制陶瓷中的“照子”就是一例。那么什么是“照子”呢，简单说就是窑工用于判别窑火温度高低的泥土胚胎。据景德镇陶瓷大学郑乃章教授研究，魏晋南北朝时已经出现照子，不过当时主要用于试验釉色；到了宋元，照子技术已经成熟，通过观察照子的烧结程度，检测窑内制品在最高烧成温度下保温时间的长短。这种技术全靠窑工的经验积累，无法定量、精确检测。

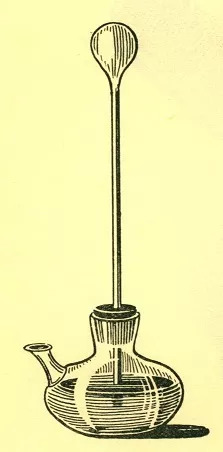
温度计的发明是西方近代科学革命的产物，而且是伽利略首先发明了一种利用空气热胀冷缩原理的气体温度计。西方在探究空气热胀冷缩及其运用方面历史悠久，早在古希腊时期，著名的希罗（Hero of Alexandria）就利用这一原理设计出了可用在神庙的自动开门机械。伽利略的气体温度计很简单，就是一根细长的玻璃管，一端开口，另一端是一鸡蛋大小的玻璃泡。使用时，先用手把玻璃泡捂热，然后让玻璃泡一端在上，把玻璃管竖直插入到水中，这便形成了一个简单的气体温度计。当外界空气上升或下降时，玻璃管中水柱就会下降或上升。如果在玻璃管上标识上刻度，便可以指示温度。尽管不清楚伽利略当时是如何标记温度的，但他在一本书中明确提到了度数。不过由于这种温度计会到受到气泡内空气温度以及外界气压的影响，误差比较大。受伽利略的启发，他的朋友、意大利帕多瓦大学的医学教授桑克托留斯（Sanctorio Sanctorius）在1612年发明了一种蛇形的气体温度计，上端的玻璃泡可以放入病人口中，从下方水柱查看病人体温的变化。这是世界上最早的体温计。

图1 伽利略的气体温度计

鉴于这种气体温度计的缺陷，1632年法国的医生让·莱伊（Jean Rey）首次把伽利略的温度计颠倒了过来，让玻璃泡在下方，并且里面充入水，以水为测温物质，温度则通过玻璃管中的水柱体现。但这种温度计玻璃管上方是开放式的，因此会受到水蒸发的影响。液体温度计后续的重大进展是由托斯卡纳的大公斐迪南二世（Ferdinand II）组织完成的，他是佛罗伦萨西芒托学院的创建人之一。他们试验了多种液体，发现酒精的热膨胀效果比较明显；同时他们把玻璃管的上端熔化封闭，这样就制成了世界上的第一支不受外界气压影响的温度计，时间是1654年。

1714年，华伦海特（Daniel Gabriel Fahrenheit）发明了水银温度计。他是一位气象仪器制造者，出生在德国，但一生大部分时间待在荷兰。水银温度计和酒精温度计各有千秋，水银的沸点为357度，故可以测量较高的温度。但由于其凝固点为零下39度，故不能测比之更低的温度。像我国内蒙古根河市，今年1月份有几天气温低至零下50多度，这种情况下水银都成固体了，自然无法使用水银温度计，但是可以使用酒精温度计，因为酒精的凝固点是零下117度。与水银温度计相反，酒精温度计不能测量较高的温度，因为酒精的沸点是78度。华伦海特不但发明了水银温度计，更重要的是开始着手确立温标。 

二、 温标的确立

温标是温度数值化的标尺，要确立温标，最重要的是找出几个基准点。1724年，华伦海特选择了三个基准点：为了避免温度中出现负数，选择了氯化铵与冰、水混合物的温度为0度；冰、水混合物温度为32度；把温度计置于人的口中或腋下，可得到人体温度96度。后来人们又做了修订，把水在标准大气压下的沸点确定为212度，这样水的冰点和沸点间算是180度，这便是华氏温标。为了纪念华伦海特，华氏温标的单位记作：℉。目前世界上的主要国家，只有美国还在沿用华氏温标。

目前全世界应用最广泛的温标系统是瑞典人摄尔修斯（Anders Celsius）确立的，他一生主要在乌普萨拉大学从事天文学研究，不过因其旁涉温度计量而大名流芳。1742年，摄尔修斯在一篇论文《对温度计上两个固定点的观察》中描述了他的温标系统，这种温标是把标准大气压下水的冰点和沸点之间划分为100度，但当时他采取的是冰点为100度，沸点为0度的方案，这样可以避免低温为负数的结果。但这一方案与人们的习惯相悖，1745年，也即摄尔修斯去年后的第二年，他的同事、瑞典植物学家林奈（Carl Linnaeus）把冰点与沸点的度数颠倒过来，这便是我们现在使用的摄氏温标。不过另有人说，做了这项颠倒工作的是摄尔修斯的继任者马丁·斯特劳莫尔（Martin Stroeme）。无论如何，这种百分温标是创始者是摄尔修斯，为了纪念他，摄氏温标的单位记作℃。显然，从绝对数值上衡量1℉≠1℃，因为摄氏温标的100份在华氏温标下是180份，它们之间有如下转换关系：F=（9C/5）+32     

     

图2 瑞典发行的纪念摄尔修斯的邮票

前述华氏温标和摄氏温标，均要依赖温度计，或者说依赖于测温物质，比如水银。可不可以找到一种不依赖于温度计的温标体系呢？可以。1848年，英国物理学家威廉·汤姆逊（William Thomson，即后来的开尔文勋爵）确立了一种新的温标——绝对温标，单位为K。此温标只有一个基准点，即绝对零度，这是冷到极限的状态，一切原子、分子的热运动都已消失，相当于摄氏温标中的零下273.15度，其分度间隔与摄氏温标相同，因此两者的转换关系为：T（K）=t(℃)+273.15。 

三、 温度计传入我国

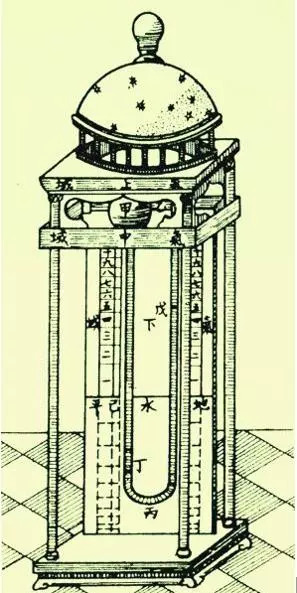
清康熙年间，在华的传教士最早把温度计相关知识引介到国内。1664年，比利时人、耶稣会传教士南怀仁（Ferdinand Verbiest）完成的《灵台仪象图》就绘有他制作的温度计。灵台就是天文台，当时的地址在如今北京建国门西南侧的古观象台。1671年，南怀仁更是完成了《验气图说》，专门谈温度计的制法、用法和原理。他制作的温度计如图3，在木架上竖立一U形玻璃管，U形管左侧上端连一玻璃球，右侧上端敞开。U形管内注入达到水平线的水（一说烧酒），玻璃球的气体受外界温度影响膨胀或收缩时，液体便会在U形管右臂或左臂上升，左右臂旁标有刻度，可以指示温度。显然，这是一种气体温度计，由于南怀仁在刻度理论上采用了错误的“天地间有三域说”，而且未能及时吸收欧洲已有的实验研究，故这种温度计不具备实测功能。

在南怀仁之后，很可能是法国来华的耶稣会士白晋（Joachim Bouvet）留下一份手稿《验气寒暑表说》，现藏梵蒂冈图书馆，中国科技大学石云里教授推测这很可能是他向康熙帝讲解西方科学的讲义之一。在这份讲义中，不但介绍了德国格里克（Otto von Guericke）、英国波义耳（Robert Boyle）就温度计研究的新进展，而且对比了新旧两种温度计。其中旧式温度计是一种气体温度计，而新式温度计便是前述斐迪南二世发明的水银温度计。

西方知识的引介、传播过程非常复杂。一方面不能高估清初传教士与皇帝的互动，康熙年间已经传入紫禁城的温度计、气压计等，到了雍正、乾隆时，他们对之仍一脸茫然，因为早年的那些仪器，早已束之高阁。另一方面不能低估好学之士吸收、仿制的能力，比如清初的黄履庄，在扬州时“因闻泰西几何比例，转捩机轴之学”，遂制出诸多奇器，其中就有“验冷热器”，即温度计。黄履庄制作温度计的知识，极有可能来自西学，至于其传播途径如何，已无从考究了。

图3 南怀仁制作的温度计

最后要说明的是，随着科学技术的发展以及现实测温条件的需要，诞生了多种多样的温

度计，大致可分为接触式与非接触式两类。在接触式温度计中，又分为像水银温度计这样的膨胀式，利用电阻随温度变化而改变的热电阻式等。在非接触式温度计中，又分为利用物体热辐射测温的辐射式，利用红外线照射导致元件温度变化的红外线温度计等。

愿这篇小文，伴随读者朋友度过一个不用关心温度的清晨、黄昏或午间。

作者史晓雷，系中国科学院自然科学史研究所副研究员

来源：史晓雷的科学网博客

本文转载自《中科院之声》微信公众号

---

十大热门文章

1 物理学咬文嚼字之一百：万物皆旋(上)

2. X射线自由电子激光单颗粒成像研究

3. X射线自由电子激光

4. 超导“小时代”之三十四：铁器新时代

5. 二胡音色的定量分析和一种改进方案

6. 云量子计算求解原子核问题

7. 周末大家谈——我和物理所

8. 忆阻器研究新进展：基于二维材料的可耐受超高温忆阻器

9. 寂静春天里的动力学（上）

10. 一种充满惊喜的二维材料

END