互信息及其在图表示学习的应用

0 前言

近些年的顶会，出现了一部分利用互信息取得很好效果的工作，它们横跨NLP、CV以及graph等领域。笔者最近也在浸淫（meng bi）这一方向，在这里和大家简要分享一些看法，如有雷同，不胜荣幸。

1 互信息简介

互信息的概念大家都不陌生，它基于香农熵，衡量了两个随机变量间的依赖程度。而不同于普通的相似性度量方法，互信息可以捕捉到变量间非线性的统计相关性，因而可以认为其能度量真实的依赖性。给定两个变量X和Z，它们的互信息如下：

第一个式子认为，互信息就是当给定变量Z时，观察者对变量X的不确定度的减少量；第二个式子中， 以及 分别是两个变量的联合分布和它们各自的边缘分布，如果是离散情况，积分号变为求和号即可。

根据第二个公式可得到互信息的一个有趣性质，即和KL散度的联系：

直观上说，a、单独考虑两个变量 b、综合考虑两个变量，如果这两种情况导致的结果差别很大，则他们关系不浅啊~ 这个性质很重要！！！ 正是它引起了一场血雨腥风。

2 互信息神经估计

互信息看似美好而强大，但是也有其明显的缺陷。最主要的一点，它很难被计算。到目前为止，只有离散的情况以及有限几种分布已知的连续的情况，互信息才可被精确计算。但聪明的人们想到了一种曲线救国的办法。

我们已经说过互信息和KL散度之间关系密切，而MINE[1]正是从这点开刀。它借鉴了另一篇文章的做法，用DV（Donsker-Varadhan）表示来逼近KL散度，即：

上式中的T属于这样一族函数：定义域是P或Q，值域是R，可以看成是对于输入的打分。也就是说，从这样一族函数中，找出使右边最大的函数T，则相当于算出了P和Q的KL散度。

用来估计互信息，就是这样：

然而，函数族的搜索空间非常大，找出符合条件的T几乎不可能。于是，作者将T参数化为神经网络 ，称为统计网络。这个公式的意义在于，它找到了一个互信息的较为紧致的下界：，这样通过梯度更新不断抬高该下界，就变相增大了X和Z间的互信息。

还有一点是关于 以及 的估计，可以使用sample。 ，联合分布，则从数据中抽取对应的X和Z； ，边缘分布的乘积，将Z进行shuffle，然后再抽取X和Z。由上面分析可知，抬高下界就相当于这样：给来自联合分布的sample打分高，给来自边缘分布乘积的sample打分低。因此，为了方便，将两者分别称为正例对和负例对。

梳理一下整体的脑回路，大概是这样：

互信息 KL散度 KL散度的DV表示 参数化下界 抬高下界

MINE这套利用神经网络估计互信息的范式，几乎成了后辈们效仿的典范，它使得评估一般性的互信息成为了可能。

3 应用

根据上一节的内容，互信息的估计涉及到以下几个问题：

• 1、X和Z的选取：你想要哪些变量间互信息最大化
• 2、 的设计：如何启发地给正例对和负例对进行打分
• 3、散度公式的选择

其中，设计模型最重要的是第一点，即明确最大化哪两者间的互信息，依据什么原理。作为目前比较火热的两篇论文：CV领域的DIM[2]和图领域的DGI[3]，它们都是依照了一篇上古时期的论文提出的Infomax准则[4]，让我们来看看这个准则

Infomax准则

其实这个准则做的事情很简单：最大化系统输入和输出间的互信息。那这么做有什么好处呢？

• 1、可以让输出包含更多关于输入的信息，而且输出会更focus在输入中较为频繁出现的模式上，即文中提到的map distortions
• 2、可以使输出的冗余度减小

关于第二点，笔者认为可以从信息论的角度考虑：系统可看成是连接输入X和输出Z的信道，而互信息 表示在信道上传输信息时，平均每个符号传递的信息量，最大化 也就等价于用更少的符号去传递更多的信息；在embedding方面，就是用更小的嵌入空间去表达更丰富的信息，因此该嵌入空间的冗余度很小。

这个准则有很多的应用，其中较为经典的是ICA（独立成分分析）。

DGI

DGI是2019年ICLR的一篇文章，它汲取了DIM的思想，将Infomax准则运用到了graph领域中。它的核心做法如下图所示

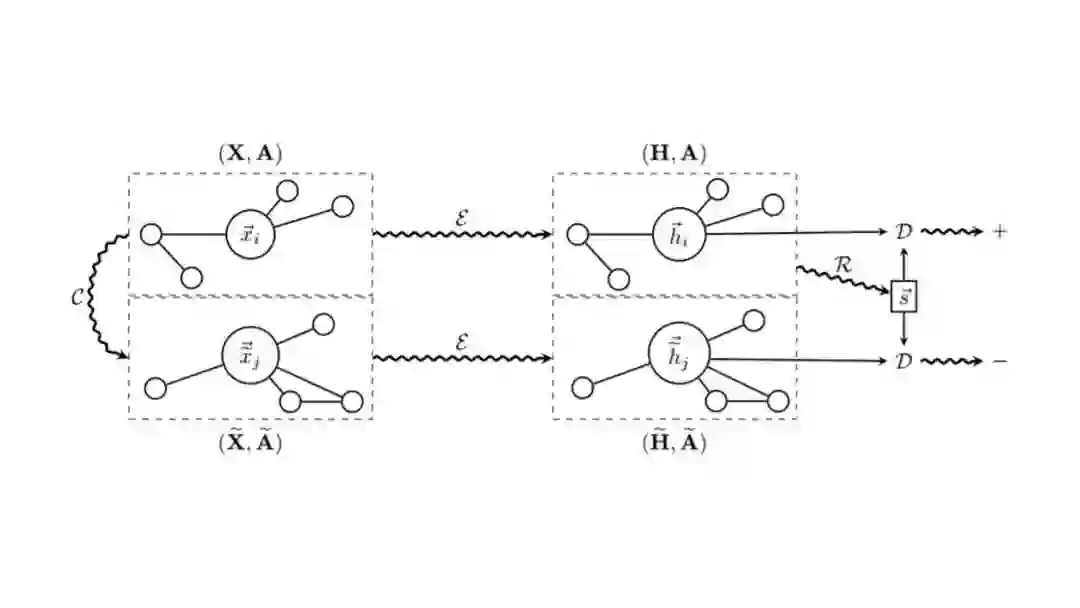
给定一张网络，其feature是X，邻接矩阵为A。经过一个编码器 （例如GCN）学到了节点表示H，之后再利用一个readout函数 （原文中是mean pooling）将节点的embedding融合成一个global级别的表示 ，和H一起组成了“local-global”对，是正例对，相当于从联合分布中采样；与此同时，设计一个打乱机制 将原图打乱（原文是保持A不变，将X打乱），得到打乱的图，经过同样的编码器 学到打乱图的节点表示 ，此时 与 组成了负例对，相当于从边缘分布的乘积中采样。之后设计一个判别器 （即 ），对正例对的打分越来越高，对负例对的打分越来越低。原文中，作者启发式地用bilinear作为判别器，即 。

按照Infomax准则，这里是将节点local表示融合成全局global表示的过程看成一个系统（即 ），最大化该系统输入（ ）和输出（ ）间的互信息，可使得全局global表示能捕捉到局部较为共性的特征，从全局和局部两个角度共同刻画了网络结构。

上面叙述的DGI的过程中，已经介绍了X和Z的选择（输入与输出）、 的设计（bilinear），还差一个散度公式的选择。那为什么会有这个考虑呢？直接用MINE里现成的基于KL散度的公式不香吗？诶，别说，还真不香！前面已经说了，DGI是汲取了CV里面DIM的思想（因为是图与推荐公众号，就不介绍DIM了哈），而DIM发现，既然将互信息转化成关于联合分布和边缘分布乘积的散度，那为什么一定是KL散度呢？其他散度公式，例如JS（Jenson-Shannon）散度不行吗？果然，高级的散度就是高级，JS散度的效果更好也更稳定。于是乎，DGI也使用JS散度来作为互信息的下界，而它更加豪横一些，先来看看它的损失函数：

是不是很熟悉？是不是很像GAN？没错，GAN的原文[5]中做了理论分析，说明了减小GAN的loss等价于减小生成数据的分布和原始数据的分布间的JS散度。而类比到DGI中，增大上式就等价于增大联合分布（ ）和边缘分布乘积（ ）间的JS散度，和MINE的处理方法有异曲同工之妙。

其他应用

上面介绍的DGI是同质网络中的方法，而在异质网络中也有两篇由它延伸的方法：HDGI[6]和DMGI[7]。它们保留了DGI最大化局部表示和全局表示间的互信息的同时，又结合了异质网络中的元路径这个概念，利用了类似于HAN[8]的层次聚合的方法，学到不同元路径的权重，进而融合在一起得到最终的节点表示。

在今年的ICLR上，Jian Tang老师的团队发表了INFOGRAP[9]，是做图分类的任务，结合了标签信息以及类似于DGI的互信息最大化操作，并且为了得到很好的知识迁移，同时最大化了监督部分的encoder和无监督部分的encoder间的互信息。今年的WWW提出的GMI[10]，很好的和图神经网络结合在一起，类似于GNN的邻居聚合，GMI最大化了节点表示与邻居节点的feature间的互信息，等同于更好地聚合了邻居信息。

4 和其他方法的联系

这类基于互信息的方法不是空穴来风的，不是拍脑袋想出来的，而应该算是当前较为流行的self-supervised里面的对比学习（contrastive learning）中的一类。对比学习的思想很简单，就是给出大量的正负例，让encoder能够在负例中正确挑选出正例，从而认为encoder抓住了object中的最unique部分，真正认清了object，有利于下游任务。对比学习最早在NLP里面开始出现，可追溯到NCE loss和负采样技术的提出，后来在CV领域发扬光大。CV里面关于正例的生成一般是同一张图片的不同augmentation，而负例则选用其他的图片，而所用的loss一般都是NCE loss。在一篇不得不提的CPC[11]这篇文章中，作者证明了NCE loss其实是和互信息有着渊源的，因此将其更名为InfoNCE，为春秋万代所传颂。。。

5 随想

上面的各种讨论，看似很华丽，其实揭开面纱后发现，这一脉关于互信息的应用无外乎就是找到联合分布和边缘分布，再选一个你喜欢的散度公式进行衡量，细细品来略有乏味。写到这里，笔者有感而发，想提出两个可能略显稚嫩的问题：

1、这一脉的方法其实是将互信息进行转化，转化成我们已知的技术，因此我们能在其中看到GAN、对比学习或是其他方法的影子，只不过用互信息进行了美化。能不能用最纯粹的信息论来解决问题？换句话说，能不能真正定义在graph中什么是信息？能否用类似Shannon的方法来进行定量刻画？

2、信息论中有很多美好的概念或是定理（比如信道容量、香农极限这种），而目前的工作感觉只是最基础地应用定义，并没有利用很多高大上的理论。那么，如何去更深刻地应用互信息于graph embedding中，使得两个领域有更深刻地交叉？

笔者水平有限，可能这两个问题已经有了答案，也可能还需要继续探索。总之，信息论是一个迷人的理论，正等待着我们去挖掘更多的宝藏！

6 参考文献

• [1] MINE: mutual information neural estimation. arXiv preprint arXiv:1801.04062, ICM 2018.
• [2] DIM: Hjelm R D , Fedorov A , Lavoie-Marchildon S , et al. Learning deep representations by mutual information estimation and maximization.
• [3] DGI:  Veličković, Petar, Fedus W , Hamilton W L , et al. Deep Graph Infomax
• [4] Infomax准则: Linsker R . Self-Organization in a Perceptual Network
• [5] GAN: Ian Goodfellow, Jean Pouget-Abadie, Mehdi Mirza , et al. Generative adversarial nets
• [6]HDGI: Yuxiang Ren, Bo Liu, Chao Huang, et al. Heterogeneous Deep Graph Infomax
• [7] DMGI: Chanyoung Park,  Donghyun Kim, Jiawei Han, et al. Unsupervised Attributed Multiplex Network Embedding
• [8] HAN:  Wang X , Ji H , Shi C , et al. Heterogeneous Graph Attention Network
• [9] INFOGRAPH: Fan-Yun Sun, Jordan Hoffmann, Vikas Verma, et al. INFOGRAPH: UNSUPERVISED AND SEMI-SUPERVISED GRAPH-LEVEL REPRESENTATION LEARNING VIA MUTUAL INFORMATION MAXIMIZATION
• [10] GMI: Zhen Peng, Wenbing Huang, Minnan Luo, et al. Graph Representation Learning via Graphical Mutual Information Maximization
• [11] CPC: Aaron van den Oord, Yazhe Li, Oriol Vinyals. Representation Learning with Contrastive Predictive Coding