三种减少卷积神经网络复杂度同时不降低性能的新方法
原论文:《Design of Efficient Convolutional Layers using Single Intra-channel Convolution, Topological Subdivisioning and Spatial "Bottleneck" Structure》
作者:Min Wang, Baoyuan Liu, Hassan Foroosh
点击文章末尾原文链接即可获取
摘要及相关背景
众所周知,深度卷积神经网络在视觉识领域别取得了非常显著的成就,但是这是以极高的计算复杂度为代价的。那么,我们可不可以发明一种全新的卷积方式,既能获得当前卷积网络的高性能,又能减少计算复杂度呢?本文作者,提出了三种改造卷积神经网络的方法,分别叫做:单通道内卷积,拓扑细分和空间瓶颈结构。这三种方法使得作者提出的模型既能达到时下最优的神经网络的性能,同时,在计算量上,VGG、ResNet-50、ResNet-101网络的计算量分别是本文提出的神经网络的计算量的42倍,4.5倍,6.5倍。
具体方法
参数说明:
本文神经网络的输入输出通道个数都是相同的,用n表示。
输入出片的尺寸为h·w
卷积核尺寸用k表示,即卷积核大小为k·k
为了使得卷积操作前后图片大小相同,仍为hw,卷积之前图片用0做padding
方法一:单通道内卷积(SIC,single intra-channel convolution)
标准卷积神经网络的操作,计算复杂度为n^2·k^2·hw
当前存在的卷积方法基本都是3-D结构的,计算复杂度分别与卷积尺寸和通道数的平方成正比,但是3-D卷积可以被看作是首先在单通道内一个2-D平面进行卷积,与此同时再进行一次映射变换。我们可以把这两个步骤拆分开来,分成2个步骤进行,这就是本文提出的方法SIC。以下是具体方法:
SIC,计算复杂度为b(nk^2+n^2)hw,由于k^2一般远小于通道数n,所以计算复杂度约为b`n^2·hw
算法2是本文提出的标准SIC,具体方法已经写得很清楚了。该算法利用了残差思想,将一个标准的卷积操作分解为顺序操作的b次通道内卷积,最后通过线性映射P组合起来。在这样操作下,计算量是原来的b/k^2。当设置b<k^2时,就能起到降低复杂度的目的。
需要指出的是,这个操作也可以不采用顺序操作而采用并行操作。作者最后也做了相应实验验证其有效性。
方法二:拓扑细分(Topological Subdivisioning)
基本思路:输出的通道的值,只和与它相邻的通道有关系。如何定义相邻呢? 对于一个输出,假设标准卷积需要30维通道来表示,在拓扑细分方法里,我们可以用一个2-D张量空间或者3-D张量空间来重新排列这30维通道。举例来说,假如排列方法为2-D:30=6*5。那么如果要输出一般意义上第13维通道上的值,那对应在2-D张量空间,即是(3,3)位置的值。此时,考虑位置(3,3)及其周围的值即可。我们用(d1,d2,...,ds),来表示张量空间,显然,他们的乘积与通道数n的关系为:d1*d2*...*ds=n。我们考虑的位置(3,3)的邻域,用(c1,c2,...,cs)表示。若c1*c2*...*cs=c的话,经过拓扑细分,能将计算复杂度降低为原来c/n。具体算法为:
拓扑细分时的卷积操作,复杂度降为标准卷积的c/n
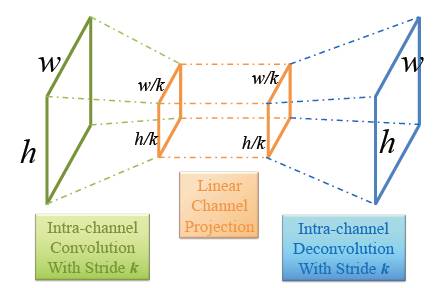
方法三:空间瓶颈结构(Spatial "Bottleneck" Structure)
这个操作比较简单,就是对于k*k的卷积操作,卷积步长设置为k,这样图片长宽就变为原来的1/k,最后为了获得与输入相同大小的输出,进行一次反卷积就可以了。下图操作图示:
瓶颈结构
实验
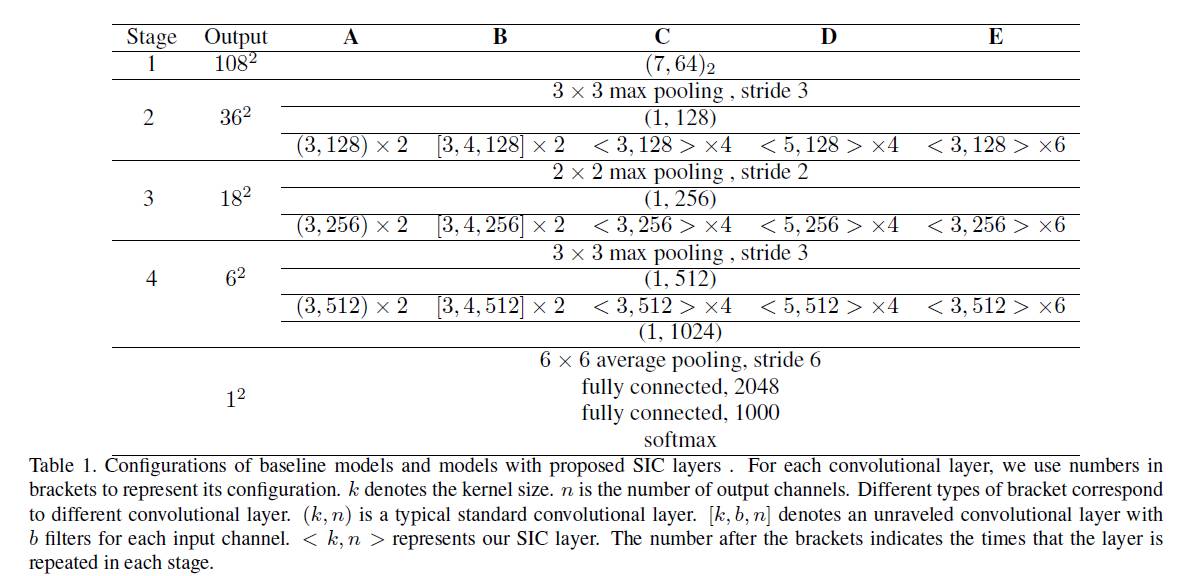
基本实验模型配置如下,一共A、B、C、D、E5个baseline。这5个模型即可说明SIC的有效性。
一,对SIC的验证:
二,对拓扑细分结构的验证
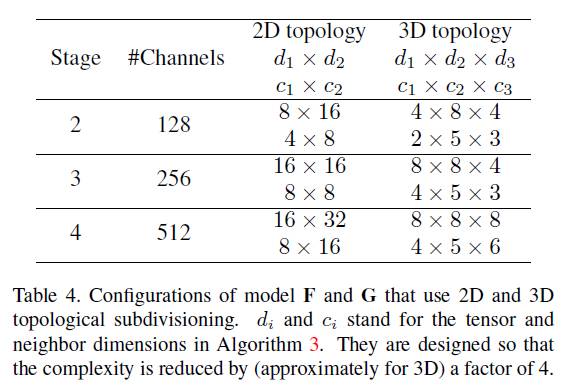
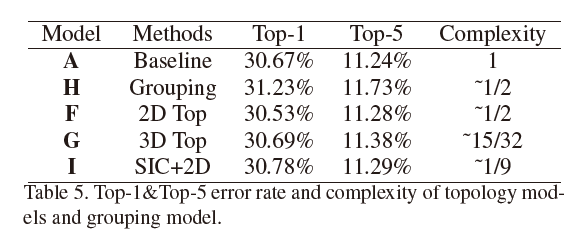
验证实验中使用到了F,G,二者从模型A改造而来,模型F和模型G的参数:
实验结果,其中模型I是SIC+2-D拓扑的模型
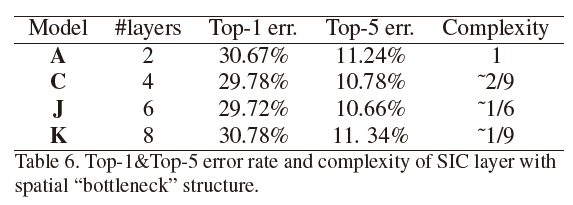
实验三、对瓶颈结构的验证
模型J、K由C改造而来。将SIC层替换成了瓶颈层。
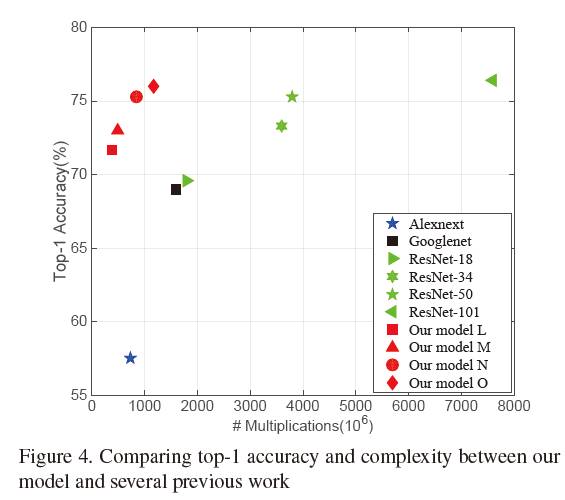
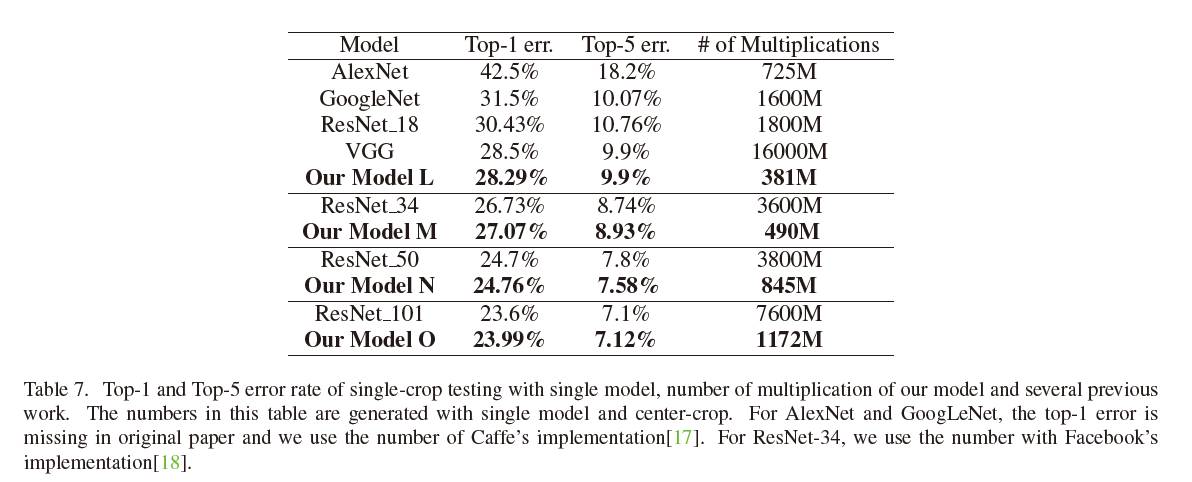
实验四、与其他标准CNN模型的对比
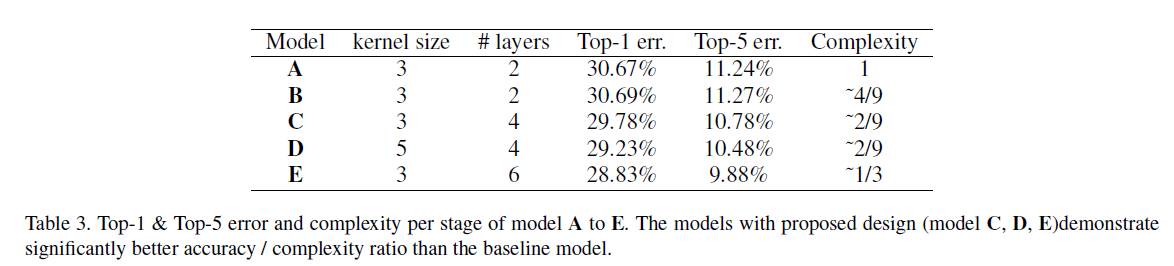
增加SIC的层数,使得最后精确度和时下最优算法相同。比较此时它们的计算复杂度。结果如下:
实验五、将得到的卷积核可视化