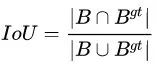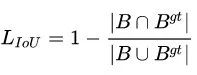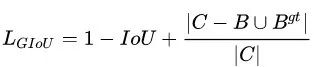基于DIou改进的YOLOv3目标检测

2020 年 2 月 8 日 计算机视觉战队

正月是农历的元月，古人称夜为“宵”，所以称正月十五为元宵节。正月十五日是一年中第一个月圆之夜，也是一元复始。

背景&引言

文中指出DIoU要比GIou更加符合目标框回归的机制，将目标与anchor之间的距离，重叠率以及尺度都考虑进去，使得目标框回归变得更加稳定，不会像IoU和GIoU一样出现训练过程中发散等问题，并且方法能够简单地迁移到现有的算法中带来性能的提升，实验在YOLOv3上提升了5.91mAP。

其中B={x,y,w,h} 是预测框，

是 ground-truth。 IoU是目标检测里面很重要的一个指标，通过预测的框和GT间的交集与并集的比例进行计算，经常用于评价bbox的优劣。但一般对bbox的精调都采用L2范数，而一些研究表明这不是最优化IoU的方法，因此出现了IoU loss 。

IoU Loss

IoU loss顾名思义就是直接通过IoU计算梯度进行回归，论文提到IoU loss的无法避免的缺点：当两个box无交集时，IoU=0，很近的无交集框和很远的无交集框的输出一样，这样就失去了梯度方向，无法优化。IoU loss的实现形式有很多种，除公式2外，还有UnitBox的交叉熵形式和IoUNet的Smooth-L1形式。

这里论文主要讨论的类似YOLO的检测网络，按照GT是否在cell判断当前bbox是否需要回归，所以可能存在无交集的情况。而一般的two stage网络，在bbox regress的时候都会卡，

不会对无交集的框进行回归。

GIoU Loss

GIou loss在IoU loss的基础上增加一个惩罚项，为包围预测框和的最小区域大小，当bbox的距离越大时，惩罚项将越大。尽管GIoU解决了IoU的梯度问题，但他仍然存在几个限制：

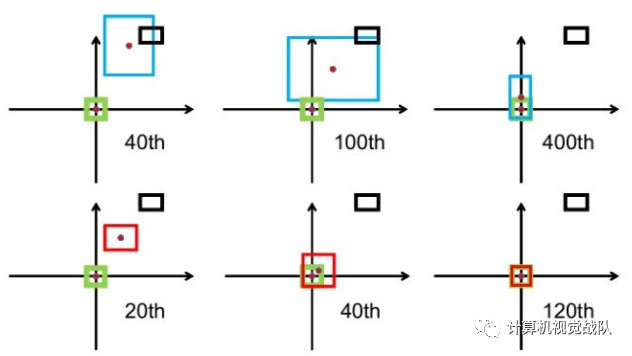
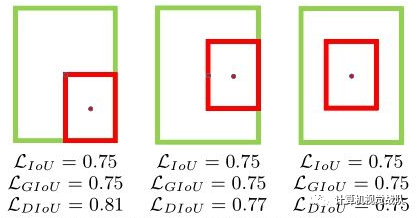
上图可以很好的来说明GIoU不稳定以及收敛很慢的原因。上图中第一行三张图展示的是GIoU的回归过程，其中绿色框为目标框，黑色框为anchor，蓝色框为不同次数的迭代后，anchor的偏移结果。第二行三张图展示的是DIoU的回归过程，其中绿色框为目标框，黑色框为anchor，红色框为不同次数的迭代后，anchor的偏移结果。从图中我们可以看到，GIoU在回归的过程中，从损失函数的形式我们发现，当IoU为0时，GIoU会先尽可能让anchor能够和目标框产生重叠，之后GIoU会渐渐退化成IoU回归策略，因此整个过程会非常缓慢而且存在发散的风险。而DIoU考虑到anchor和目标之间的中心点距离，可以更快更有效更稳定的进行回归。

如上图中的包含情况，GIoU会退化成IoU(三个位置预测框和gt框所包围的最小面积相同，惩罚项c保持一致，梯度发散)。由于很大程度依赖IoU项，GIoU需要更多的迭代次数来收敛，特别是水平和垂直的bbox（后面会分析）。一般地，GIoU loss不能很好地收敛SOTA算法，反而造成不好的结果。

综合上面的分析，论文提出Distance-IoU(DIoU) loss，简单地在IoU loss基础上添加一个惩罚项，该惩罚项用于最小化两个bbox的中心点距离。如图1所示，DIoU收敛速度和效果都很好，而且DIoU能够用于NMS的计算中，不仅考虑了重叠区域，还考虑了中心点距离。另外，论文考虑bbox的三要素，重叠区域，中心点距离和长宽比，进一步提出了Complete IoU(CIoU) loss，收敛更快，效果更好。

知识回顾

IoU and GIoU Losses

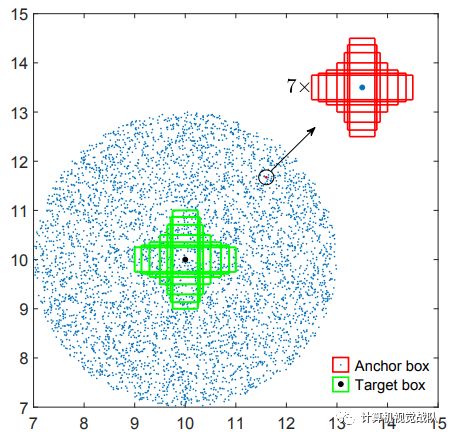
为了全面地分析IoU loss和GIoU的性能，论文进行了模拟实验，模拟不同的距离、尺寸和长宽比的bbox的回归情况，如下图所示：

绿色框代表仿真实验需要回归的七个不同尺度的目标框，七个目标框的中心点坐标都是（10 * 10）；
蓝色的点代表了所有anchor的中心点，中心点的分布如上图所示，各个方向都有，各种距离都有，当然每个anchor的一个中心点都包含有七个不同面积的anchor框。而且每个面积的anchor框又有七种不同的比例尺寸。因此一共有5000个蓝色点，对应5000*7*7个anchor框，并且每个anchor框都需要回归到七个gt目标框上，因此一共有5000*7*7*7个回归案例。

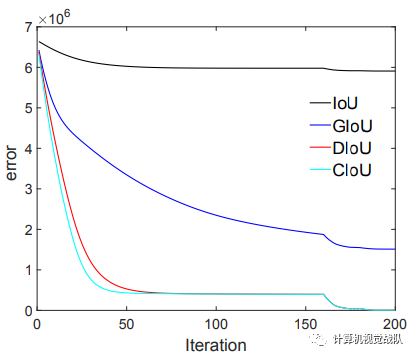
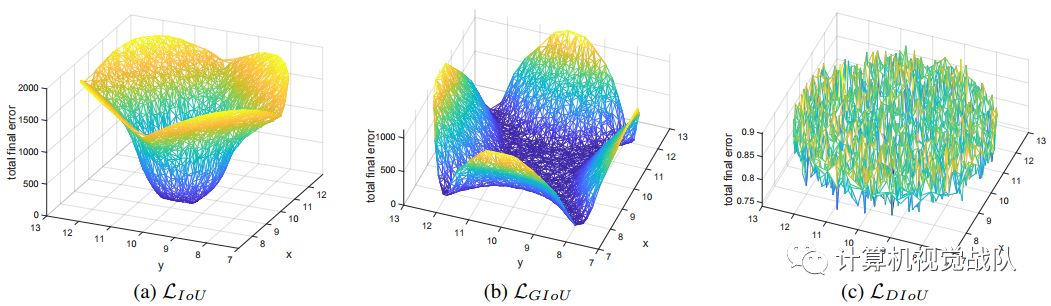
最终的实验结果如下：图中展示的训练同样的步数后（200步），IoU,GIoU以及本文提出的DIoU、CIoU作为loss的情况下，每个anchor的误差分布。

IoU：从IoU误差的曲线我们可以发现，anchor越靠近边缘，误差越大，那些与目标框没有重叠的anchor基本无法回归；
GIoU：从GIoU误差的曲线我们可以发现，对于一些没有重叠的anchor，GIoU的表现要比IoU更好。但是由于GIoU仍然严重的依赖IoU，因此在两个垂直方向，误差很大，基本很难收敛，这就是GIoU不稳定的原因；
DIoU：从DIoU误差的曲线我们可以发现，对于不同距离，方向，面积和比例的anchor，DIoU都能做到较好的回归。

具体伪算法步骤如下：

对于预测框，当前迭代（current iteration epochs = t）回合, 可以通过下式获得：

给定一个loss函数，可以通过梯度下降来模拟bbox优化的过程。对于预测的bbox ，为阶段的结果，( )'为对的梯度，使用来加速收敛。bbox的优化评价使用 -norm，共训练200轮，error曲线如下图所示：

论文将5000个中心点上的bbox在最后阶段的total error进行了可视化。IoU loss只对与target box有交集的bbox有效，因为无交集的bbox的梯度为0。而GIoU由于增加了惩罚函数，中间大部分区域错误率明显减少，但是垂直和水平的区域依然保持着高的error，这是由于GIoU的惩罚项经常很小甚至为0，导致训练需要更多的迭代来收敛。