数据科学中的机器学习基础和进展

2018 年 2 月 27 日 中国计算机学会 大数据专家委员会

CCF于1月11日发布了最新一期《中国计算机科学技术发展报告》，对可群智协同计算、软件智能化开发技术等11个方向的研究进展做了详细介绍和讨论。我们将分期分享报告中的精彩内容，加入CCF会员登录CCF官网，可在数字图书馆栏目下载和浏览。

1 引言

近年来，随着大数据研究热潮的出现，数据科学受到了越来越多的关注。热潮引发了学界、工业界以及各领域关于数据科学的热烈讨论，争论涉及基础的数据科学的概念体系、研究方法和理论基础的界定等诸多方面。关于数据科学的概念，目前有一些不同的观点：有学者认为数据科学是新一代的统计学习，也有学者认为数据科学是一些跨学科领域的总和等。根据文献[1]，本文分别从高层和学科等角度给出数据科学的若干定义。

定义1. （数据科学，高层定义）数据科学是关于数据的科学和研究。

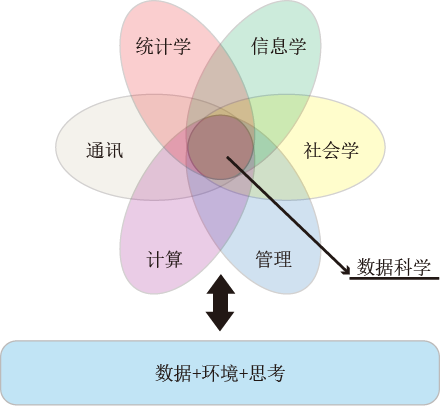
定义2. （数据科学，学科定义）数据科学是一个融合了统计学、信息学、计算、通讯、管理以及社会学的新的交叉学科，其研究主体为数据及其环境，其目标是将数据转化为洞察力以及决策，采用的方法论以及思路是将数据转化为知识进而转化为智慧。

根据上述的定义，文献[1]中给出了数据科学的学科表示：

数据科学={统计学+信息学+计算+通讯+社会学+管理}|{数据+环境+思考} （1）

其中“|”表示条件依赖于，图1给出了由定义2定义的数据科学的韦恩图。

图1. 数据科学的韦恩图

数据科学的最终产物是数据产品[1]，其定义如下：

定义3. （数据产品）数据产品是由数据产生的可交付物或者是由数据使能或驱动的产物。数据产品可以是一种发现、预测、服务、推荐、决策洞察力、见解、模型、模式、范式、工具或者系统。最终极数据产品的价值是知识、智力、智慧以及决策。

1.1 数据科学与大数据

近年来，数据科学与大数据几乎总是同时出现的，谈到大数据的文章通常也会同时谈到数据科学。大数据具有5V特点：体量大（Volume）、速度快（Velocity）、种类多样（Variety）、真实性（Veracity）、价值密度低（Value）[2]。毋庸置疑的是，大数据蕴藏着丰富的价值。然而，从其5V特点中也可以看出，从大数据中得出有用的信息、知识乃至智慧是极具挑战性的。大数据与数据科学两者关系紧密，相辅相成。大数据的兴起以及各领域对大数据的关注，推动了数据科学的发展；数据科学是大数据研究发展的重要工具和手段，为大数据分析提供了强大的保障，两者相互结合，可以产生创造出巨大的价值。

1.2 数据科学与机器学习

数据科学涉及统计学，信息学，计算，通讯，社会学，管理等多个知识领域的交叉和融合。数据科学的理论以这些学科的理论为基础。目前数据科学所涉及的数据分析技术包括：统计学、计算机科学、机器学习、数据可视化等多方面。

机器学习是数据科学的重要组成部分，也是人工智能的一个重要分支。机器学习算法的主要目标是对数据进行分析，得出规律，利用规律对未知的数据进行预测。可以看到，机器学习算法的目标与数据科学的目标在本质上是一致的，即从数据中挖掘或者统计出有用的信息、知识乃至智慧。机器学习领域中的深度学习技术能有效地分析处理大数据。近些年深度学习技术的兴起，使得机器学习作为数据科学中的一种技术，得到了更多的关注。本文主要针对目前若干种具有挑战的数据分析任务，给出数据科学中机器学习技术研究的最新进展。

1.3 数据科学时代机器学习面临的挑战

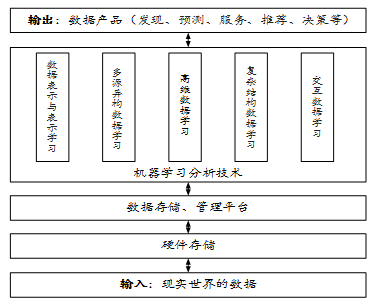
综上所述，数据科学的终极任务是从数据中得出有用的信息和知识。然而，近些年，随着大数据的兴起以及数据分析任务越来越复杂，传统的机器学习技术已经越来越不能适用于目前的很多数据分析任务。图2给出了在数据科学时代，数据科学的整体研究框图以及机器学习在其中的位置。

整体来说，现实世界的大数据经过数据收集步骤，首先会存储到硬件设备上，物理的数据存储设备包括单台计算机、服务器、集群以及数据中心等，根据具体的数据量情况，采用的硬件设备也会有所不同。大数据时代对数据的存储设备提出了更高的要求，如需要保证数据的稳定性和安全性等。

当大数据分布式存储在不同的机器上时，会给数据的分析带来困难。因此，有一部分学者研究分布式的大数据管理与分析平台，如近年来大家使用比较多的Hadoop、Spark、Storm平台等。此外，由于大数据领域，非结构化数据的不断增长，对数据库存储的要求也会越来越高，例如Hadoop平台下的HBase就是一个面向非关系型数据的数据库系统。

在数据存储、数据管理平台的基础上，本报告重点关注数据科学中的机器学习数据分析技术，主要从以下六个方面对研究进展进行介绍：

（1）大数据中的数据表示与表示学习技术 数据表示是所有数据分析任务的基础，好的数据特征表示可以使得整个分析任务获得更好的性能。这部分重点回顾了基于深度学习的特征表示方法以及国内外进展情况。

（2）高维数据学习 目前对高维数据的学习，主要可以考虑采用特征选择、维度约简、数据采样等方法。这部分将重点介绍特征选择和维度约简等技术的最新进展。

（3）多源异构数据学习 大数据不仅仅是体量大，还存在复杂的结构。多源异构属于复杂数据中的一种。随着数据采集设备的发展，通常一个目标存在多种表示，即构成目标的多模态（多视图）表示。这部分重点给出多模态分类器学习、多模态子空间学习和多模态相似性度量等相关工作的研究进展。

（4）复杂结构数据学习 在很多任务中，数据存在天然的结构信息，如何从数据中学出或者恢复出这样的结构信息是结构学习关注的重点，这部分将从判别式和生成式结构学习两方面对相关工作进行介绍。

（5）交互式数据学习 交互式大数据是由多个行为实体共同作用产生的。在该方面，本文将主要从强化学习和多agent博弈等方面对相关研究进行介绍。

（6）非独立同分布学习 是指任何面向非独立同分布（Non-IID）的数据的学习方法。本文将从理论，方法与应用等不同角度阐述非独立同分布学习。

图2. 数据科学的研究结构图

2 国内外研究现状

下面主要对数据科学中的机器学习技术研究进展进行介绍，包括数据表示与表示学习、高维数据学习、多源异构数据学习、结构学习以及交互数据学习等五个方面。图3中给出了数据分析技术与数据类型之间的相互关系。

首先，所有数据分析任务的基础是数据表示与表示学习，这里将重点介绍监督式表示学习、半监督式表示学习以及无监督式的表示学习。然后针对大数据时代出现的多种具有挑战性的数据类型，介绍相应的数据分析技术。具体的数据类型包括多源异构数据、高维数据、复杂结构数据以及交互式数据。针对多源异构数据，从多视图学习、多模态特征选择、多模态子空间学习以及多模态距离度量等四个方面，介绍相关的数据处理技术。在高维数据分析方法，主要介绍数据的维度约简技术，包括特征选择、降维、采样等方法。此外，针对复杂结构的大数据，从生成式以及判别式结构学习的角度，介绍数据的结构学习方法。最后，介绍交互式数据的处理，包括强化学习、多agent学习以及博弈论等方面的工作。

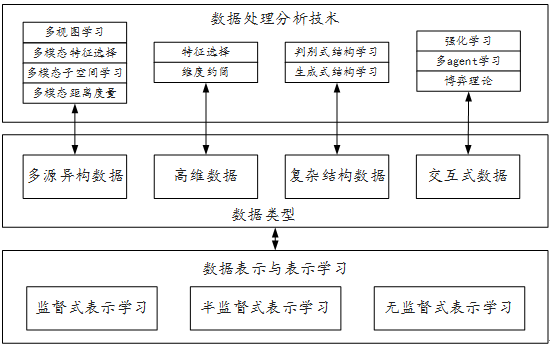
图3. 数据科学中的机器学习技术

2.1 数据表示与表示学习

数据表示一直都是计算机学科的研究重点和数据科学发展的基石。正是因为有了数据表示，各种各样的数据（文本、声音、图像等等）才能在计算机中进行存储、分析和运算。在机器学习领域，数据表示更是重中之重。所谓数据表示（或称为特征表示），指的是用一组符号或数字，即特征向量去描述一个对象，并且能够体现这个对象的一些特性、结构和分布。数据表示的好处在于通过抽取数据中有意义的信息，一方面减小数据体量，另一方面方便计算机分析和用户解释。好的数据表示往往能够较大幅度地缩小数据的体量，同时保留原始数据中重要的特性，捕获数据潜在可解释因素的后验分布，并且保持对随机噪音的鲁棒性。

数据表示发展早期的代表是特征工程，即通过使用领域知识或者专家知识来创造特征，进而对数据进行表示，在机器学习领域常用的手工特征即为典型代表。但特征工程对人工和先验知识有高度依赖，在实际应用中并不高效，这引发了表示学习的研究。表示学习能够从原始低级的感知数据直接学习高级抽象的特征表示，更利于后续的数据分析和处理。

表示学习的研究领域很广，很多研究其实都可以归结为表示学习，比如子空间学习、度量学习、流形学习、稀疏编码以及现在盛行的深度学习等。深度学习是表示学习的成功典范，通过分层非线性的特征学习，能够很好的表示数据，并且在语音识别、自然语言处理和图像识别等领域获得了巨大成功。在大数据时代，表示学习也逐渐从监督式学习向半监督式、无监督式学习方向发展。

本文主要从深度学习角度去探究表示学习的发展现状，并从监督式表示学习、半监督式表示学习和无监督式表示学习三方面进行阐述。

2.1.1 监督式表示学习

目前，常用的全连接神经网络（Fully connected neural networks）、卷积神经网络（Convolutional neural networks，简称CNN）和循环神经网络（Recurrent neural networks，简称RNN）等可以看作是监督式表示学习的代表。通过带标签的数据进行网络训练，能够从数据中学到很好的特征表示。

全连接神经网络（也称多层感知机）包含输入层、隐含层和输出层，通过误差反向传播算法（Error backpropagation，简称BP）对网络进行训练。全连接网络适用于向量形式的输入数据，通过不断地线性加权和非线性映射，能够学到任务相关的更好特征表示。得益于新的激活函数的设计，如ReLU和maxout等，传统全连接网络中的梯度消失现象能得到有效控制，这使得全连接网络有更好的应用和发展。

卷积神经网络主要针对图像数据进行设计，能够对其进行很好的特征表示学习，在图像识别领域取得了巨大成功。近年来，学者相继提出了很多典型的网络结构，如1998年LeCun提出的用于手写字符识别的网络LeNet [7]；2012年在ILSVRC （Large scale visual recognition challenge）比赛中大放异彩的AlexNet [8]；Simonyan等人于2014年提出的层数更深的VGG网络[9]；随后Google研究人员引入Inception结构，进而提出的GoogLeNet [10,11]；2015年来自微软的何凯明等人通过跳跃结构和残差学习，将网络深度推向极致的ResNet [12]。基于类似的思想，2017年Huang 等人提出的DenseNet将网络中所有层两两进行连接，网络的每一层都接受其前面所有层的特征作为输入，一方面减轻了梯度消失现象，另一方面也极大地减少了网络参数[136]。除了图像识别，卷积神经网络在语音识别[13,14]和自然语言处理[15,16]等领域也有不错的应用。

循环神经网络能够对序列数据进行很好的特征表示学习，在自然语言处理和序列数据处理中有广泛应用。和传统神经网络不同的是，循环神经网络会对网络前面的信息进行记忆并应用到当前输出的计算中。也就是说，RNN中隐藏层的节点之间是有连接的，其输入不仅包含输入层的输出还包括上一时刻隐藏层的输出。RNN中最重要的是门控机制，代表性的有长短期记忆单元（Long short-term memory, 简称LSTM）[17]和门循环单元（Gated recurrent units, 简称GRUs）[18]。RNN已成功应用到包括语言模型和文本生成[19,20,21,22]、机器翻译[23,24,25,26]、语音识别[27]、图像描述生成[28,29]等诸多领域。同时，结合了RNN和CNN的网络结构也成功应用在如目标识别[30]、显著性检测[31]、行为识别[32]、行人重识别[33]等计算机视觉任务中。

2.1.2 半监督式表示学习

半监督式表示学习在表示学习过程中除使用带标签的数据外，还辅助使用无标签的数据。这样做既可以充分利用大量无标签的数据，又能够提高模型的泛化能力。Weston等人通过将半监督正则项以三种不同的模式加入到网络结构中，将现有的半监督嵌入技术应用到了神经网络中，实现了神经网络的半监督学习[34]。Kingma等人基于变分自编码器提出了一个半监督的深度生成模型，并通过变分EM算法、随机梯度变分贝叶斯及随机反向传播等方法对该模型进行训练[37]。Rasmus等人在梯形网络的基础上同时最小化监督损失函数和无监督损失函数的和，避免了逐层预训练的操作[35]。针对文本文档的表示学习，Ranzato等人提出了一个半监督的自动编码器深度网络[36]。Miyato等人在目标函数中引入了每一个训练样本的预测分布的局部平滑，提高了监督和半监督方法的性能。Yang 等人基于图嵌入（Graph embedding）提出了一个半监督的学习框架，通过直推式或者归纳式的嵌入来预测样本的标签及其在图上的近邻[137]。Thomas N. Kipf 针对图结构的数据专门设计了一个卷积神经网络的变体，即图卷积网络（Graph convolutional networks，简称GCN）。GCN把所有操作都放在图上进行，能快速且可扩展地完成图上节点的半监督分类任务[138]。

2.1.3 无监督式表示学习

现有深度学习的训练往往需要大量的标记数据，但是大量标记数据的获取需要耗费昂贵的代价。如何有效利用庞大的未标记数据是一个大的挑战，这就促使了无监督式表示学习的发展，也代表了深度表示学习的一个重要发展方向。很多学者已经在这个方向进行了探索，不少无监督表示学习方法已经相继被提出。这些方法大致可分为三类：

基于自动编码器的表示学习 自动编码器（Auto-encoder）[39]是一种尽可能复现输入信号的神经网络，通过编码器encoder对输入进行编码，然后再将编码输入到解码器decoder进行解码得到输出，通过调整encoder和decoder的参数，最小化输入输出的重构误差。通过这种无监督的方式，可以得到输入数据的一个特征表示。通过自动编码器进行表示学习的研究工作有很多，大致可分为稀疏自动编码器（Sparse auto-encoders）[40,41]、去噪自动编码器（Denoising auto-encoders）[42]、收缩自动编码器（Contractive auto-encoders）[43]、预测稀疏分解（Predictive sparse decomposition）[44]、深度自动编码器（Deep auto-encoders）[45]等。

基于生成对抗网络GAN的表示学习 Goodfellow于2014年提出了生成对抗网络（Generative Adversarial Networks，简称GANs）[46]。随后，GANs便以风靡之势席卷整个人工智能领域。GAN由一个生成器和一个判别器构成，利用二人零和博弈的思想，通过对抗学习的方式进行训练，进而估测出数据样本的潜在分布并生成新的数据样本。通过无监督对抗学习的方式，GAN除了能生成新的样本外，还可以用来进行表示学习。Radford 等人提出了深度卷积生成对抗网络DCGANs，将判别器学到的特征用于图像分类任务。随后，Chen等人提出了信息最大化生成对抗网络InfoGAN，同样通过完全无监督的方式学习具有可解释性且松的特征表示[47]。Donahue 等人提出了一个双向的对抗生成网络BiGAN [48]，在这个网络里，除包含了一个标准的生成器G外，还增加了一个编码器E（即反向的生成器），用于将数据映射到潜在的特征表示。

基于先验知识的表示学习 基于先验知识的无监督表示学习通过一些先验知识、结构信息或者聚类的方式获得伪标签，然后利用这个伪标签训练深度网络。Doersch等人利用空间上下文信息来学习一个丰富的视觉表示，具体为从一张图像上随机抽取成对的图像块，然后训练一个卷积神经网络来预测第二个图像块相对于第一个图像块的相对位置[49]。Wang等人通过无标记的视频数据来学习视觉表示，其核心思想是通过无监督的跟踪算法找到相邻接的两个图像块，并保证它们具有相似的视觉特征表示，借此来训练网络[50]。Yang提出了一个循环的框架来联合地学习深度特征表示和图像聚类，其核心思想是好的特征表示有利于聚类，同时聚类结果又能为表示学习提供监督信号。该框架通过一种端到端的方式能够在无监督条件下学到一个很好的特征表示[51]。Xie 提出的深度嵌入聚类DEC方法使用了类似的想法，不同的是DEC利用深度自动编码器学习一个低维的特征空间，然后在这个低维的特征空间里迭代优化一个聚类目标函数[52]。

2.2 高维数据学习

高维大数据指的是维度过高，用传统的学习方法无法处理的数据，属于大数据子类别。对高维数据研究主要包括高维数据特征选择和高维数据降维等。经过特征维度约简后的数据可采用传统的机器学习算法来处理。

2.2.1 高维数据特征选择

特征选择任务的目标是从全部特征中通过特定的评价标准与搜索策略来选取一个最优的特征子集，使后续的学习模型有更好的效果。在大数据时代，如果特征维度高到传统的机器学习算法无法处理，则可以采用特征选择的方式，来对维度约简，使得传统算法仍然得以适用。已有的特征选择算法，根据评价函数的不同可分为：过滤式（Filter）、封装式（Wrapper）和嵌入式（Embedding）[53]。过滤式特征选择方法通过分析特征自身的特点，设计特定评估标准来衡量特征的重要性，其特征选择过程与分类模型无关；封装式特征选择方法的特点是对选择的特征子集学习相应的分类模型，分类表现用来衡量所选特征子集的质量好坏；嵌入式特征选择方法将特征选择与分类过程相结合，是前两类方法的折中。第一种过滤式的方法，因为不需要进行分类器训练，所以时间效率最高的。其主要思路是采用一些特征与类别之间的相关性衡量指标来进行特征选择。例如，Kira等人提出了ReliefF方法[54]，通过样本间的近邻距离来给特征赋予权重，权重超过预设阈值的即被选择为最终特征。其他类别可分性的衡量标准还有Fisher Score[55]、 Laplacian Score[56]等。此外，从概率相关性角度来看，Peng等人[57]引入信息论中的互信息来衡量特征与类别之间的相关性，提出了最小冗余最大相关的衡量方法mRMR。Tibshirani于1996提出的Lasso方法[58]，是一种通过稀疏性学习求解优化问题来选择特征的方法，其主要思想是通过最小化带L1稀疏约束的线性拟合误差，来学习稀疏的特征选择向量，然后选择对应向量元素大于0的特征形成特征集合。

尽管基于过滤式的方法时间性能较优，但是对于特定的任务来说，选择的特征不一定是最优的，在大数据环境下，设计高效的第二类和第三类方法，在提高分析任务性能等方面会更有优势[59]。

2.2.2 高维数据降维技术

高维数据降维方法的主要思想是在原始的高维数据中寻找一个低维的公共子空间，使得将样本投影到学习得到的子空间后，得到的低维特征具有一些特性（如同类样本的特征距离近，不同类样本的特征距离远等）。第一类代表性的降维算法有线性的子空间降维方法，包括主成分分析（ Principal Component Analysis，简称PCA）[60]和线性判别分析（ Linear Discriminant Analysis，简称LDA）[60]等算法。PCA算法的目标是学习得到一个子空间，使得样本的特征在子空间中的方差最大化，从而样本在子空间中的分布尽可能分散。LDA算法的目标是使得在学习得到的投影后的空间中，同类样本的距离比较近，而不同类样本的距离比较远。第二类是非线性的降维学习算法，包括基于核函数的降维算法和基于流形学习的降维算法等。基于核函数的算法假设非线性可分的样本在映射到一个更高维度时是可分的，其解决的方案是引入核函数，经典的线性降维方法基本都可以扩展为基于核函数的降维方法，例如核主成分分析（KPCA）[63]和核判别性分析（KDA）[64]等。第三类是研究者关注较多的流形学习方法。该方法假设数据样本服从流形分布，即数据虽然表现出来是高维的，但其本质上是低维的。流形学习算法中经典的算法包括ISOMAP [65] 、局部线性嵌入（Locally linear embedding）[66]、LE（Laplacian eigenmaps）[67]、图嵌入（Graph embedding）[61]等。ISOMAP方法首先计算原始空间中样本的测地线距离，然后采用MDS算法找到一个子空间，使得原始空间中的距离关系在子空间中得到保持。在保持原始样本之间的距离关系时，它采用的是基于全局的距离计算方法。与ISOMAP不同，其它算法采用的是局部距离，保持的是样本的局部近邻关系。在大数据时代，这些算法面临的主要挑战是如何对体量大的、有可能动态更新的数据进行快速有效的维度约简。近期还有研究者提出了一些在线子空间学习的算法[68][69]，这些研究尚处于起步阶段。

2.2.3 高维数据随机采样

2.3 多源异构数据学习

近年来，随着数据采集设备的发展和新型采集手段的出现，人们可以获得大量的产生于不同数据源或特征集合的数据，其中每一个数据源或特征集合构成一个模态，并且各个模态的数据分布有较大的差异，这样就形成了多模态数据[70]。在计算机视觉应用中，多模态数据种类繁多且规模较大，如（含视频、音频与文字的）多媒体、多模态医学影像、视频监控中的多摄像头视频数据等。如何对这些大量的多源、多模态、多介质数据进行有效地分析是非常重要的。目前，许多国家战略性文件都对多模态数据分析有所涉及，如在中国工业和信息化部于2014年出版的《大数据白皮书》中，就明确提到的大数据分析技术需要突破的两方面之一是，“对非结构化数据进行分析，将海量复杂多源的语音、图像和视频数据转化为机器可识别的、具有明确语义的信息，进而从中提取有用的知识”。因此，多模态学习作为机器学习领域的重要分支，具有非常重要的理论与应用研究价值。

在目前的研究阶段，由于多模态数据通常表现为结构复杂、数据量大、并具有领域知识，使得对于其内在结构分析、有用数据的提取，语义信息的挖掘成为极具挑战的研究问题。对于特定的应用问题，例如多视角的行为识别，多模态数据会对同一个行为从多种不同的角度去进行描述，通过多视图学习有效融合不同模态的特征信息，在很大程度上能够提高学习器的泛化能力。多模态数据约简旨在降低数据的复杂性，其主要方法包括多模态特征选择和子空间学习。针对约简的数据，跨模态度量学习可以帮助挖掘多模态样本间的关联关系。下面主要从多视图学习、多模态特征选择、多模态子空间学习和跨模态度量等四个方面来对国内外研究现状进行讨论。

2.3.1 多视图学习

多视图学习旨在利用视图之间的关系或相互学习来提高目标任务的学习效率。它起源于1998年卡耐基梅隆大学 Blum 和 Mitchell [71]提出的协同训练（Co-training），即两个视图通过相互学习来提高对未标记样本的预测精度。协同训练要求数据的每个视图必须具备两个条件： 1）充分冗余（Sufficient and redundant）；2）条件独立（Conditional independent）。然而后续研究表明该条件过于严格，2005年Balcan等人[72]提出了较弱的膨胀性假设，即两个充分冗余的模态满足膨胀性且与此同时单模态分类器须能正确分类标记样本。此外，Wang和Zhou[132]证明了双模态不需要充分冗余，只需两个学习器具有较大的差异性，协同训练也同样有效。这大大弱化了协同训练的充分条件，为多模态半监督学习应用提供了理论支撑。目前，国内外研究者提出了许多的多视图半监督学习方法[73]。它们分别对每个视图训练一个分类器，并对不同视图的未标记样本预测结果作一致性或平均一致性的约束。常见的方法包括 Chaudhuri 等人[74]将典型相关性分析（CCA）作为多个视图的相关性度量，学习多个视图相关性最大的潜在子空间，并进行聚类。除了CCA， Fisher 判别性分析（FDA）[75]和隐含狄利克雷分配模型（Latent Dirichlet Allocation，简称LDA）[76]也被用于学习多视图的潜在表示。

2.3.2 多模态数据特征选择

然而，以上描述的多模态学习方法并不适用于高维多模态数据，有可能产生维度灾难。而且，特别是对于维度极高的数据，大量的冗余特征会增加学习任务、样本相似性计算及模态间关系度量的难度，同时增加计算负担。因而，近年来，出现了一些多模态维度约简方法，如多模态特征选择和多模态子空间学习，来解决多模态高维数据分析问题。这些方法通过减少特征表示的维数，来提高学习任务的效率。多模态特征选择方法是在传统的特征选择基础上，利用不同模态间的耦合关系来选择重要性特征的方法。根据不同模态间关系的度量方式的不同，它们可分为3类：1）基于模态层、联合模态层与聚类结构，2）联合模态层，3）样本层的特征选择方法。针对第一类模态层的方法，Feng等人[77]提出了一种无监督的多模态特征选择方法，对每个模态衡量一个特定的权重，同一模态内进行最小化线性拟合误差与基于L2,1范数的正则化约束，不同模态间通过简单加权的方式来联合地学习每个模态的特征选择向量。对于第二类联合模态层与聚类结构的方法，Wang等人[78]提出了基于聚类结构的多模态特征选择方法，即同一模态内通过结构稀疏来鼓励不同的聚类选择不同的特征，而不同模态间约束其具有共同的聚类结构。对于第三类联合模态层与样本层的方法，Yang等人分别运用联合局部与全局分析[139]、基于低秩与稀疏学习的方法[133]，来衡量特征层、样本层与模态层的重要性。

2.3.3 多模态数据子空间学习

与多模态特征选择不同，多模态子空间学习的目的通常是通过学习某个隐含空间，将原始高维数据用某个低维子空间进行表示。近年来，在该研究领域也取得了一系列的研究成果。Gu等人[79]采用L2,1范数的约束，提出了一种能够将子空间学习和特征选择结合的框架，并将其应用于人脸识别。Zhang等人[80]针对大多数线性子空间学习方法不能有效判别图像局部在图像识别应用中的重要性的问题，提出了一种基于稀疏编码和特征分组的线性学习方法。White等人[81]针对多模态数据，提出了一种有效的多模态数据子空间学习方法和一种能解决“数据缺失”资源映射问题的基于低秩约束的方法。Kim等人[82]针对缺失数据子空间学习的问题，提出了一种基于 Elastic-Net 规则化的方法。Li等人[136]针对数据表示应用，提出了一种结构化的子空间学习方法。该方法将图像理解和特征学习结合到同一框架中，其学习到的子空间能够有效缩小低级特征和高级语义之间的鸿沟。

2.3.4 跨模态数据度量

跨模态异构度量主要解决的科学问题是如何学习有效的距离度量函数用于度量不同模态（异构）数据样本之间的距离。目前，主流的跨模态度量方法为学习其公共子空间，如Mignon和Jurie[83]提出了一种同时优化同类和不同类跨模态距离约束的度量学习方法。Zhai等人[137]提出了一种针对半监督场景的异构度量学习方法。该方法的特点是同时考虑了公共子空间中样本分布的全局一致性和局部平滑性。Zhou 等人[138]将局部线性嵌入（LLE）方法进行了扩展，提出了将样本分布的局部线性结构和成对的距离约束整合到统一框架中进行异构度量的学习方法。除了上述基于公共子空间的异构度量学习方法外，Zhen等人[85]提出了一种基于概率图模型框架的跨模态相似性度量学习方法，其思想是同时学习不同模态下样本的二值表示，且同时采用成对的相似性约束进行学习。在[86]中，Kang等人提出了基于低秩双线性度量的异构度量学习方，其学习目标是使得学习到的度量函数满足一系列成对的同类和不同类跨模态相似性约束。

2.4 复杂结构数据学习

近年来，结构学习已经广泛应用在具有天然结构属性的数据分析任务中。以计算机视觉应用为例，由于图像视频中较强的结构特点，国内外研究者已经针对若干应用，如图像分割[87]、图像目标识别[88,89]、视频目标跟踪[90,91]和人类活动识别[92,93]等，开展了关于结构学习的研究。特别地，按照模型类型，以往关于结构学习的工作可分为两大类：以结构化支持向量机为代表[94,95]的判别式结构学习和以贝叶斯理论为指导[104,105]的生成式结构学习。

2.4.1 判别式结构学习

关于判别式结构学习，Taskar等人[94]结合最大间隔马尔可夫网和核学习二者的优势，通过结构化序列最小化（SMO）进行求解，其优点在于不但能处理高维数据，还能学习结构数据间的相关关系；其缺点是收敛速度慢，这一点在马尔可夫网络中尤为明显。随后，Taskar 等人[96]采用鞍点的方法对问题进行求解，其目的在于提高求解效率，但仍需较大内存用以计算。 Ratliff 等人[97]采用次梯度方法来进行求解。当步长为常数的时候，次梯度方法具有线性收敛的性质。针对图像目标识别，Blaschko和Lampert[88]使用结构化学习来学习图像和其内部目标框之间的映射，使其能够同时建模局部和全局的上下文信息。Desai等人[98]使用结构化支持向量机来学习目标类之间的空间关系，旨在获得一张图像上所有目标框的同步分类器。Shen等人[99]提出统一结构化学习方法来同时解决人体姿态估计和服装属性分类问题。现有很多结构学习算法需要一个强的充分条件，即具有复杂结构的训练数据均需要被完全标记。Lou等人[100]针对这个问题提出一种新方法，能够从部分标记的数据中学习一个可以接近从完整标记数据中学习的结果。最近，Domke[101]观察发现如果推理问题是平滑的，通过增加熵条件，结构学习的目标可以约简成传统的（非结构的）逻辑回归问题。基于这个观察，结构能量函数可以从线性函数扩展到任意函数类，只要这个函数类存在一个先验知识来最小化逻辑损失。

2.4.2 生成式结构学习

关于生成式结构学习，Tsamardinos 等人[102]提出了最大-最小爬山法。该方法结合了局部学习法与打分搜索法，在重构贝叶斯网络的基础上，利用爬山法确定无向边的方向。Pedro等人[103]提出了最大-最小蚁群优化算法（MMACO），利用蚁群优化法确定无向边的方向。Koivisto等人[104]利用动态规划方法计算贝叶斯网络中每条边的后验概率。为了进一步提高效率，Eaton等人[105]在[104]的基础上，将动态规划与马尔可夫链蒙特卡洛方法相结合，克服了[104]中方法的时间、空间复杂度过高的缺点。此外，De Campos等人[104]结合MDL、AIC、BID三种不同的评价标准对结构进行打分，并利用分支界限法约束最终学习到的结构。Teyssier 等人[107]在给定节点顺序的前提下进行贝叶斯网络结构学习，不仅缩小了结构的搜索空间，还避免了无环检查。

2.5 交互数据学习

分析数据的产生机理可以发现，主要存在两种类型的数据：一是以物理世界为研究目标的，通过对自然现象、工业生产观测所得到的科学（或生产）数据；二是以对商业活动、人类生活、社会交往为研究目标，通过企业CRM或互联网应用所得到的交互型数据。

科学数据的产生过程，不以分析者的意志为转移，其目的是发现和揭示自然规律。对交互型数据的分析，会影响人（或其他参与者，如政府及企业）的行为和决策，进而导致后续交互型数据的变化。交互型数据是由一个或多个行为实体发生交互产生的。这些行为实体既与环境（包括各种信息系统）进行交互，相互之间也进行交互，产生大量的交互型数据。根据交互实体为一个或多个，本报告将从单交互实体最优策略的学习技术和多交互实体决策的博弈建模及学习技术等两方面对交互型数据的进展进行阐述。

2.5.1单交互实体最优策略的学习技术

目前针对单实体交互型任务的学习问题，国内外研究者已经提出了大量的强化学习算法，以期快速学习到最优策略。传统的强化学习主要关注的是基于值表、线性函数、核函数、浅层神经网络的表示技术。面对大规模数据和任务空间的学习问题，传统表示方法较为低效，取而代之是结合深度表示的强化学习，即深度强化学习。例如针对常见的交互型游戏，如“雅达利”（Atari），Google DeepMind团队提出了结合深度卷积网络的DQN算法(Deep Q-Networks) [108]，其改进版本在Atari游戏平台中49款游戏达到了人类专家水平[109]。针对“我的世界（Minecraft）”游戏，Oh等人采用了基于存储的深度强化学习，其实验效果优于现有的深度强化学习结构[110]。针对围棋（Go）游戏，AlphaGo通过深度策略网络缩小搜索广度、通过深度评估网络缩小搜索深度，并结合蒙特卡洛树搜索，战胜了韩国著名围棋九段选手李世石，在全世界范围内引起轰动[111]。

2.5.2多交互实体决策的博弈建模及推理

上节提到的强化学习方法只能处理有1-2个行为实体参与的学习问题。对于存在多个行为实体的交互型数据任务，目前尚缺乏有效的解决方案。在此类交互型数据复杂决策中，需要事先构造博弈模型，并通过相应的算法进行均衡策略的求解。如有研究者对众包用户之间的潜在博弈关系进行建模，并给出了在相应机制下的均衡解[113]。交互型数据同时具有序列决策和自利博弈的性质，因此也需要基于博弈的多agent学习技术来学习交互实体的最优策略。例如有研究者针对竞合型任务的多agent强化学习，采用马尔可夫博弈进行建模[117]。然而这样的博弈模型会出现学习效率较低的问题。近年来,有研究者研究基于迁移的多agent强化学习，迁移相似博弈的均衡策略[118]，或者迁移博弈约简情况下相似马尔可夫决策过程（MDP）的值函数[119]。这些研究大大加快了agent的学习速度。虽然这些工作在加快学习速度方面取得了一定的进展，但是面对大规模复杂任务场景，现有方法仍然面临着计算开销过大的问题。

综上所述，对于交互型数据的研究基本处于空白，尚缺少对交互型数据分析的理论和技术体系。然而，传统的强化学习、在线学习、多agent学习和博弈论，在近年来取得了长足的发展。相关理论和技术发展，已为建立交互型数据分析的理论和技术体系奠定了初步的基础。

2.6 非独立同分布学习

非独立同分布学习（Non-IID Learning）是指任何面向非独立同分布（Non-IID）的数据的学习方法[1]。经典的数据分析、机器学习、人工智能、模式识别、图像处理、信号处理等理论系统和工具大多是建立在独立同分布（IID，Independent and Identical Distributed）的数据假设之下的。这些工作从样本、属性、值等不同层面对于数据的独立性和分布的一致性进行假设。这样的假设在处理小规模的单一数据时有效地简化了问题的复杂性，可以使相关方法取得很好的效果。然而，对于复杂的大数据与小数据，独立同分布的假设已经无法反应其数据的复杂性。使用以独立同分布假设为基础的理论系统和工具对复杂数据进行分析，会得到不完整甚至错误的结论。因此，非独立同分布学习是大数据处理的一项重要理论基础。

非独立同分布学习的核心思想与任务是学习复杂数据中的多层次、多类型的耦合关系（Coupling Relationships，即非独立性）和异构性（Heterogeneity，即非同分布性）。非独立同分布学习是数据科学（包括大数据分析、机器学习、统计学习）中的基本问题，涉及多源异构数据、各种大/小的复杂数据、行为数据、高维数据、交互学习等各种问题。非独立同分布学习各类与各领域的数据。

下面，从非独立同分布学习的理论研究、非独立同分布学习在特定领域的方法和应用两个方面对国内外研究现状进行简要讨论。

2.6.1非独立同分布学习的理论研究

关于非独立同分布数据的研究已有多年的历史，主要涉及基于条件概率的统计学习、基于隐关系与隐变量的学习、基于从非独立同分布向独立同分布数据转换的分析等。在开展了一系列的深入研究的基础上，Cao[146]对于非独立同分布学习问题与理论进行了系统性地阐述。非独立同分布学习理论[146]认为复杂数据（可能是大数据、也可能是小数据）中存在着从属性值、属性到样本（甚至数据源、方法、学习结果等）的层次化的耦合关系与异构性，这些耦合关系与异构性表现为不同的形式、类型、层次、结构、分布、关系等。这里所指的耦合关系可能包括已经研究得比较清楚的相关性（Correlation）、关联性（Association）以及依赖关系（Dependency），也可能包括目前还未能很好的形式化的关系，比如经济、社会、文化关系，定性与定量关系，隐式与显式关系、确定与不确定关系等。具有这种层次化的复杂耦合关系与异构性的数据被称之为非独立同分布数据。

非独立同分布数据的特点与复杂性是经典的基于独立同分布假设的数据处理与学习理论与方法所不能有效解决的。同时，Cao[146]对非独立同分布学习的需求、挑战和机遇进行了比较系统的探讨。此后，Cao[147]对非独立同分布学习中的非独立性学习（即耦合学习，Coupling Learning）进行了进一步的研究。其从数据属性值、数据属性、数据样本、数据源、学习方法/模型、学习结果（如模式）等多个层次与方面分析讨论了如何层次化地对不同类型的耦合关系进行建模和检测，并且给出了耦合学习的形式化定义和框架。

此外，Steinwart [148] 等人也对SVM在学习非独立数据时的学习能力进行了理论分析。对于非同分布数据的理论研究主要集中在数据分布的变化和迁移过程上。Mohri和Rostamizadeh [149] 给出了非独立同分布过程的稳定边界。Ralaivola等人 [150] 提出了针对非独立同分布数据的PAC-贝叶斯学习边界，从理论上分析了针对非同分布数据的学习性能上界，并应用到了β混合过程的分析中。Steinwart和Christmann [151] 提出了面向非同分布观测对象的快速学习方法。

2.6.2 非独立同分布学习方法与应用

近些年来，随着对非独立同分布学习理论的深入与系统研究，一系列基于非独立同分布数据假设的学习方法、模型、与应用得以提出、实现和应用。从对数据的处理流程来说，这些非独立同分布学习方法可以分成两大类。第一类方法属于间接的非独立同分布学习。这一类方法关注于将非独立同分布的数据转化、表示为独立同分布的形式，然后采用现有的机器学习方法在转化后的独立同分布空间中进行学习。第二类方法属于直接的非独立同分布学习。其直接对复杂的非独立同分布数据进行分析、建模和学习。本节分别就这两类方法中的现有工作进行分析讨论。

2.6.3 间接非独立同分布学习方法与应用

间接的非独立同分布学习方法与应用一般建立一个从非独立同分布数据到独立同分布数据的空间转换，在转换后的独立同分布空间上进行分析与学习。Wang等人[152][153]提出了对非独立同分布数据中的层次化耦合关系的学习方法，并将耦合关系显式的嵌入到数据的相似度空间之中。具体来说，该方法测量了数据值之间在分布上的相关关系，数据属性之间的共现关系，以及在此基础上的数据样本之间耦合关系。Wang等人[154]分析了非独立同分布数据中属性间的高阶耦合关系，进一步增强了对非独立同分布的表示能力。此后，Jian等人[155]研究了数据值之间层次化的复杂耦合关系，并将其嵌入（Embedding）表达在向量空间之中。在这些非独立同分布的表示基础之上，分类、聚类、回归等经典的基于独立同分布假设的机器学习方法都可以适用。实验结果表明，相较于在非独立同分布数据上直接使用基于独立同分布假设的机器学习方法，在转化后的数据上使用这些方法得到了显著的性能提升[156][157]。

2.6.4 直接非独立同分布学习方法与应用

直接针对非独立同分布数据进行建模与学习需要考虑数据与领域的具体特点加以进行。针对不同领域的数据特点，直接对非独立同分布数据建模学习的方法有着显著的区别。在群体行为分析领域[171]，Cao等人[158]和Song等人[159]分别对金融市场交易者行为中的个体行为耦合序列、群体行为间的耦合等行为非独立同分布性进行建模分析，建立基于耦合隐马尔可夫模型的群体异常行为分析模型，并捕捉到市场的合谋操纵行为。Cao等人[160]进一步利用深度模型对于金融市场中复杂的耦合关系进行建模学习。在图像处理领域，Xu等人[161]捕捉了社交图片的属性内和属性间的耦合关系，从非独立同分布的角度对社交图片进行了分析。Shi等人[162]对图像和多源数据的耦合关系进行学习，从而提升了基于图片的阿茲海默症诊断性能。在社区发现领域，Fan等人[163][164][165]利用非参贝叶斯方法和统计连接关系对网络中成员的关联关系进行学习，有效的捕获了网络中的复杂耦合关系，从而提升了社区发现的性能。在异常检测领域，Pang等人[166][167]通过对层次化的特征值之间的耦合关系进行建模来对非独立同分布数据的异常样本进行检测以及特征选择。Pang等人[168]进一步对同质的耦合关系进行建模学习，从而消除了非独立同分布数据异常检测中噪音的干扰。Pang等人[166][167][168]同时处理了特征冗余、高噪声、高维等问题。在推荐系统领域，Cao [169][170]对用户非独立同分布性、产品非独立同分布性、用户和产品间存在的隐式与显式的非独立同分布性进行了系统探讨，提出了非独立同分布推荐系统的框架以及初步应用，显著提升了推荐系统的处理能力与性能[157]。

此外，非独立同分布学习研究还在诸多领域得以展开，比如对象与模式关系分析[172]，基于文本中关键词之间[173]、关键词对间关系学习[174]的文本分析，基于关键词关系的检索查询方法[175，176]，分类[156]，医学图像中异常检测[177]等。从以上的工作可以看出，虽然针对不同的数据特点所提出的非独立同分布学习有着显著的区别，但是这些方法的核心思想都是捕获和学习非独立同分布数据中的复杂的耦合关系和异构性。

3 发展趋势与展望

数据科学是一门融合了多种学科的科学。本文是从大数据时代数据分析的挑战这一角度，主要介绍了数据科学在机器学习领域的最新进展。

未来的数据科学研究，需要依赖研究者对各类型的大数据分析，与各领域（包括生物，天文，地理，商业等各个领域）产生的大数据打交道，了解数据的产生机理与机制，对复杂的数据建模，提出新的解决大数据科学问题的方法论。

本文介绍了数据科学中与机器学习相关的五个方面。在数据表示方面，尽管目前深度学习大幅提升了传统数据特征表示方法的性能，数据表示仍然有可以进一步发展的空间。例如，对于异构数据，时间序列数据，关系型数据等的表示方法，仍然存在着诸多值得进一步研究的课题。硬件计算设备的发展，给解决高维数据的分析任务带来了便利。传统的高维数据学习方法主要是从特征选择、数据降维等角度对该问题进行处理。然而，数据大部分时候不仅高维，还可能存在异构多模态、数据量大等特点，使得传统的方法无法处理。针对这些多种挑战同时存在的高维数据处理，目前还有较大的研究空间。关于多源异构数据的研究，近几年涌现了非常多的研究工作，后续的发展方向包括跨模态的数据生成融合等。不同模态下的数据的公共成分分析，模态差异消除和相似性学习等仍是值得进一步研究的方向。数据的结构关系学习是解决大数据复杂结构的重要手段之一。已有的数据结构关系学习方法主要用于解决小数据量的问题。在大数据时代，数据量增大，结构学习仍然是一个待解决的问题。数据的产生通常都是带有人为干预的，可能涉及到多个agent相互协作和博弈。近年来，强化学习、多agent博弈得到了比较大的关注。对于交互式数据的学习，强化学习、多agent博弈是值得继续研究的方向，与它相关的理论研究以及技术体系也有待完善。

4 结束语

数据科学是解决大数据问题的基础科学，得到了国内外研究者的重点关注。本文先介绍了数据科学的发展简史、概念体系与组成，接着较系统地介绍了在大数据时代，数据科学在大数据的几个重要问题上的最新进展。目前国内外的研究者在该领域都做出了令人兴奋的工作，希望本文可以对国内外的研究者有所启发，引导他们在数据科学领域做出更多有创新性的工作。

本报告的整理得到国家自然科学基金委员会大数据重点项目群项目、军民共用重大研究计划“面向大数据的知识表示、推理、在线学习理论及应用研究”(编号：61432008, U1435214)的支持。霍静、宋锦华、李文斌、杨尚东、祁磊、庄韫恺、于谦、杨丽等同志参加了整理工作，在此一并致谢。

参考文献：

[1] Cao L. Data science: a comprehensive overview[J]. ACM Computing Surveys (CSUR), 2017, 50(3): 43.

[2] Hilbert M. Big data for development: A review of promises and challenges[J]. Development Policy Review, 2016, 34(1): 135-174.

[3] Cao L., Fayyad U. Data science: Challenges and directions[J]. Commun. ACM, 2016: 1-9.

[4] Cao L. Data science: nature and pitfalls[J]. IEEE Intelligent Systems, 2016, 31(5): 66-75.

[5] Dhar V. Data science and prediction[J]. Communications of the ACM, 2013, 56(12): 64-73.

[6] Schutt R, O'Neil C. Doing data science: Straight talk from the frontline[M]. " O'Reilly Media, Inc.", 2013.

[7] LeCun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324.

[8] Krizhevsky A, Sutskever I, Hinton G E. ImageNet classification with deep convolutional neural networks[C]//Advances in neural information processing systems. 2012: 1097-1105.

[9] Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition[J]. arXiv preprint arXiv:1409.1556, 2014.

[10] Szegedy C, Liu W, Jia Y, et al. Going deeper with convolutions[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2015: 1-9.

[11] Szegedy C, Vanhoucke V, Ioffe S, et al. Rethinking the inception architecture for computer vision[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2016: 2818-2826.

[12] He K, Zhang X, Ren S, et al. Deep residual learning for image recognition[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2016: 770-778.

[13] Abdel-Hamid O, Mohamed A, Jiang H, et al. Convolutional neural networks for speech recognition[J]. IEEE/ACM transactions on audio, speech, and language processing, 2014, 22(10): 1533-1545.

[14] Huang J T, Li J, Gong Y. An analysis of convolutional neural networks for speech recognition[C]//Acoustics, Speech and Signal Processing (ICASSP), 2015 IEEE International Conference on. IEEE, 2015: 4989-4993.

[15] Kim Y. Convolutional neural networks for sentence classification[J]. arXiv preprint arXiv:1408.5882, 2014.

[16] Zhang X, Zhao J, LeCun Y. Character-level convolutional networks for text classification[C]//Advances in neural information processing systems. 2015: 649-657.

[17] Hochreiter S, Schmidhuber J. LSTM can solve hard long time lag problems[C]//Advances in neural information processing systems. 1997: 473-479.

[18] Cho K, Van Merriënboer B, Bahdanau D, et al. On the properties of neural machine translation: Encoder-decoder approaches[J]. arXiv preprint arXiv:1409.1259, 2014.

[19] Sutskever I, Martens J, Hinton G E. Generating text with recurrent neural networks[C]//Proceedings of the 28th international conference on machine learning (ICML-11). 2011: 1017-1024.

[20] Mikolov T, Karafiát M, Burget L, et al. Recurrent neural network based language model[C]//Interspeech. 2010, 2: 3.

[21] Mikolov T, Kombrink S, Burget L, et al. Extensions of recurrent neural network language model[C]//Acoustics, Speech and Signal Processing (ICASSP), 2011 IEEE International Conference on. IEEE, 2011: 5528-5531.

[22] Kim Y, Jernite Y, Sontag D, et al. Character-Aware Neural Language Models[C]//AAAI. 2016: 2741-2749.

[23] Liu S, Yang N, Li M, et al. A recursive recurrent neural network for statistical machine translation[C]. Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics (ACL) 2014.

[24] Sutskever I, Vinyals O, Le Q V. Sequence to sequence learning with neural networks[C]//Advances in neural information processing systems. 2014: 3104-3112.

[25] Auli M, Galley M, Quirk C, et al. Joint Language and Translation Modeling with Recurrent Neural Networks[C]// The 2013 Conference on Empirical Methods on Natural Language Processing (EMNLP). 2013, 3(8):

[26] Wu Y, Schuster M, Chen Z, et al. Google's neural machine translation system: Bridging the gap between human and machine translation[J]. arXiv preprint arXiv:1609.08144, 2016.

[27] Graves A, Jaitly N. Towards end-to-end speech recognition with recurrent neural networks[C]//Proceedings of the 31st International Conference on Machine Learning (ICML-14). 2014: 1764-1772.

[28] Mao J, Xu W, Yang Y, et al. Deep captioning with multimodal recurrent neural networks (m-rnn)[J]. arXiv preprint arXiv:1412.6632, 2014.

[29] Xu K, Ba J, Kiros R, et al. Show, attend and tell: Neural image caption generation with visual attention[C]//International conference on Machine Learning. 2015: 2048-2057.

[30] Visin F, Kastner K, Cho K, et al. ReNet: A recurrent neural network based alternative to convolutional networks[J]. Computer Science, 2015, 25(7):2983-2996.

[31] Kuen J, Wang Z, Wang G. Recurrent Attentional Networks for Saliency Detection[C]// Computer Vision and Pattern Recognition. IEEE, 2016:3668-3677.

[32] Deng Z, Vahdat A, Hu H, et al. Structure Inference Machines: Recurrent Neural Networks for Analyzing Relations in Group Activity Recognition. IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 2016:4772-4781.

[33] Mclaughlin N, Rincon J M D, Miller P. Recurrent convolutional network for video-based person re-identification[C]// Computer Vision and Pattern Recognition. IEEE, 2016:1325-1334.

[34] Weston J, Ratle F, Mobahi H, et al. Deep learning via semi-supervised embedding[M]//Neural Networks: Tricks of the Trade. Springer Berlin Heidelberg, 2012: 639-655.

[35] Rasmus A, Berglund M, Honkala M, et al. Semi-supervised learning with ladder networks[C]//Advances in neural information processing systems. 2015: 3546-3554.

[36] Ranzato M A, Szummer M. Semi-supervised learning of compact document representations with deep networks[C]//Proceedings of the 25th international conference on Machine learning. ACM, 2008: 792-799.

[37] Kingma D P, Mohamed S, Rezende D J, et al. Semi-supervised learning with deep generative models[C]//Advances in Neural Information Processing Systems. 2014: 3581-3589.

[38] Miyato T, Maeda S, Koyama M, et al. Distributional smoothing by virtual adversarial examples[J]. stat, 2015, 1050: 2.

[39] Hinton G E, Zemel R S. Autoencoders, minimum description length and Helmholtz free energy[C]//Advances in neural information processing systems. 1994: 3-10.

[40] Poultney C, Chopra S, Cun Y L. Efficient learning of sparse representations with an energy-based model[C]//Advances in neural information processing systems. 2007: 1137-1144.

[41] Le Q V. Building high-level features using large scale unsupervised learning[C]//Acoustics, Speech and Signal Processing (ICASSP), 2013 IEEE International Conference on. IEEE, 2013: 8595-8598.

[42] Vincent P, Larochelle H, Lajoie I, et al. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion[J]. Journal of Machine Learning Research, 2010, 11(Dec): 3371-3408.

[43] Rifai S, Vincent P, Muller X, et al. Contractive auto-encoders: Explicit invariance during feature extraction[C]//Proceedings of the 28th international conference on machine learning (ICML-11). 2011: 833-840.

[44] Kavukcuoglu K, Ranzato M A, LeCun Y. Fast inference in sparse coding algorithms with applications to object recognition[J]. arXiv preprint arXiv:1010.3467, 2010.

[45] Hinton G E, Salakhutdinov R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786): 504-507.

[46] Goodfellow I, Pouget-Abadie J, Mirza M, et al. Generative adversarial nets[C]//Advances in neural information processing systems. 2014: 2672-2680.

[47] Chen X, Duan Y, Houthooft R, et al. Infogan: Interpretable representation learning by information maximizing generative adversarial nets[C]//Advances in neural information processing systems. 2016: 2172-2180.

[48] Donahue J, Krähenbühl P, Darrell T. Adversarial feature learning[J]. arXiv preprint arXiv:1605.09782, 2016.

[49] Doersch C, Gupta A, Efros A A. Unsupervised visual representation learning by context prediction[C]//Proceedings of the IEEE international conference on computer vision. 2015: 1422-1430.

[50] Wang X, Gupta A. Unsupervised learning of visual representations using videos[C]//Proceedings of the IEEE international conference on computer vision. 2015: 2794-2802.

[51] Yang J, Parikh D, Batra D. Joint unsupervised learning of deep representations and image clusters[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2016: 5147-5156.

[52] Xie J, Girshick R, Farhadi A. Unsupervised deep embedding for clustering analysis[C]//International Conference on Machine Learning. 2016: 478-487.

[53] Guyon, I., Elisseeff, A., 2003. An introduction to variable and feature selection. The Journal of Machine Learning Research 3, 1157–1182

[54] Kononenko, I., Apr. 1994. Estimating attributes: analysis and extensions of RELIEF, in: Proc. European Conference on Machine Learning, Catania, Italy. pp. 171–182

[55] Duda, R.O., Hart, P.E., Stork, D.G., 2012. Pattern classification. John Wiley & Sons.

[56] He, X., Cai, D., Niyogi, P., Dec. 2005. Laplacian score for feature selection, in: Proc. Advances in Neural Information Processing Systems, Vancouver, B.C.. pp. 507–514.

[57] Peng, H., Long, F., Ding, C., Aug. 2005. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. Pattern Analysis and Machine Intelligence, IEEE Transactions on 27, 1226– 1238.

[58] Tibshirani, R., 1996. Regression shrinkage and selection via the Lasso. Journal of the Royal Statistical Society (Series B) 58, 267–288.

[59] Lim N, Lederer J. Efficient feature selection with large and high-dimensional data[J]. arXiv preprint arXiv:1609.07195, 2016.

[60] Maaten, L., Postma, E., Herik, H. Dimensionality reduction: A comparative review. Journal of Machine Learning Research 10.

[61] Yan, S., Xu, D., Zhang, B., Zhang, H.J., Yang, Q., Lin, S., 2007. Graph embedding and extensions: a general framework for dimensionality reduction. Pattern Analysis and Machine Intelligence, IEEE Transactions on 29, 40–51.

[63] Xu Y, Zhang D, Song F, et al. A method for speeding up feature extraction based on KPCA[J]. Neurocomputing, 2007, 70(4): 1056-1061.

[64] Yang J, Frangi A F, Yang J, et al. KPCA plus LDA: a complete kernel Fisher discriminant framework for feature extraction and recognition[J]. IEEE transactions on pattern analysis and machine intelligence, 2005, 27(2): 230-244.

[65] Tenenbaum J B, De Silva V, Langford J C. A global geometric framework for nonlinear dimensionality reduction[J]. Science, 2000, 290(5500): 2319-2323.

[66] Roweis S T, Saul L K. Nonlinear dimensionality reduction by locally linear embedding[J]. Science, 2000, 290(5500): 2323-2326.

[67] Belkin M, Niyogi P. Laplacian eigenmaps for dimensionality reduction and data representation[J]. Neural computation, 2003, 15(6): 1373-1396.

[68] Giampouras P V, Rontogiannis A A, Themelis K E, et al. Online Low-Rank Subspace Learning from Incomplete Data: A Bayesian View[J]. arXiv preprint arXiv:1602.03670, 2016.

[69] Sheikholesalmi F, Giannakis G B. Online subspace learning and nonlinear classification of Big Data with misses[C]//Information Sciences and Systems (CISS), 2015 49th Annual Conference on. IEEE, 2015: 1-6.

[70] Xu, C., Tao, D. and Xu, C., A survey on multi-view learning. ArXiv e-prints 1304.5634, 2013.

[71] A. Blum and T. Mitchell. Combining labeled and unlabeled data with co-training. In Annual Conference on Learning Theory (COLT), 1998

[72] M. Balcan, A. Blum, and K. Yang. Co-training and expansion: towards bridging theory and practice. Advances in neural information processing systems (NIPS), 89-96, 2005.

[73] G. Li, C. Kuiyu, S. Hoi. Multi-view semi-supervised learning with consensus. IEEE transaction on knowledge and data engineering (TKDE), vol.24, no.11, pp.2040-2051, 2012.

[74] K. Chaudhuri, S. M. Kakade, K. Livescu, K. Sridharan. Multi-view clustering via canonical correlation analysis. In Proc. of the 26th International Conference on Machine Learning (ICML),2009.

[75] T. Diethe, D. Hardoon, J. Shawe-Taylor, Multi-view Fisher discriminant analysis, In NIPS workshop on learning from multiple sources, 2008.

[76] E. Xing, R. Yan, A. Hauptmann. Mining associated text and images with dual-wing harmoniums. In Uncertainty in Artificial Intelligence (UAI), 2005.

[77] Y. Feng, J. Xiao, Y. Zhuang, and X. Liu. Adaptive unsupervised multi-view feature selection for visual concept recognition. In Asian Conference on Computer Vision (ACCV) 2012.

[78] Wang, H., Nie, F., Huang, H., Jun. 2013. Multi-view clustering and feature learning via structured sparsity, in: Proceedings of the 30th International Conference on Machine Learning, Atlanta. pp. 352–360.

[79] Gu Q, Li Z, Han J. Joint feature selection and subspace learning. International Joint Conference on Artificial Intelligence (IJCAI). 2011, 22(1): 1294.

[80] Zhang L, Zhu P, Hu Q, et al. A linear subspace learning approach via sparse coding. Computer Vision (ICCV), 2011 IEEE International Conference on. IEEE, 2011: 755-761.

[81] White M, Zhang X, Schuurmans D, et al. Convex multi-view subspace learning. Advances in Neural Information Processing Systems. 2012: 1673-1681.

[82] Kim E, Lee M, Oh S. Elastic-Net Regularization of Singular Values for Robust Subspace Learning. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2015: 915-923.

[83] Mignon A, Jurie F. CMML: a new metric learning approach for cross modal matching[C]. Asian Conference on Computer Vision. 2012: 14 pages.

[84] Wu L, Du L, Liu B, et al. Heterogeneous Metric Learning with Content-based Regularization for Software Artifact Retrieval[C]. Data Mining (ICDM), 2014 IEEE International Conference on. IEEE, 2014: 610-619.

[85] Zhen Y, Rai P, Zha H, et al. Cross-Modal Similarity Learning via Pairs, Preferences, and Active Supervision[C]. AAAI Conference on Artificial Intelligence (AAAI). 2015: 3203-3209.

[86] Kang C, Liao S, He Y, et al. Cross-modal similarity learning: A low rank bilinear formulation[C]. Proceedings of the 24th ACM International on Conference on Information and Knowledge Management. ACM, 2015: 1251-1260

[87] Lucchi A, Li Y, Smith K, et al. Structured image segmentation using kernelized features. In Proc. European Conference on Computer Vision (ECCV), 2012: 400-413.

[88] M. Blaschko and C. Lampert. Learning to Localize Objects with Structured Output Regression [M]. In Proc. European Conference on Computer Vision (ECCV), 2008.

[89] Blaschko M B, Lampert C H. Object Localization with Global and Local Context Kernels. In Proc. British Machine Vision Conference (BMVC). 2009: 1-11.

[90] Yao R, Shi Q, Shen C, et al. Robust tracking with weighted online structured learning. In Proc. European Conference on Computer Vision (ECCV), 2012: 158-172.

[91] Hare, S., Saffari, A., Torr, P.: Struck: Structured output tracking with kernels. In International Conference on Computer Vision (ICCV), 2011: 263–270.

[92] Lan T, Wang Y, Yang W, et al. Beyond actions: Discriminative models for contextual group activities. In Proc. Advances in Neural Information Processing Systems (NIPS), 2010: 1216-1224.

[93] Niebles J C, Chen C W, Fei-Fei L. Modeling temporal structure of decomposable motion segments for activity classification. In Proc. European Conference on Computer Vision (ECCV), 2010: 392-405.

[94] Taskar B, Guestrin C, and Koller D, Max-margin Markov networks, In Proc. Advances in Neural Information Processing Systems Conference (NIPS), 2003.

[95] Tsochantaridis I, Joachims T, Hofmann T, et al. Large margin methods for structured and interdependent output variables. Journal of Machine Learning Research. 2005: 1453-1484.

[96] Taskar B, Lacoste-Julien S, Jordan M. Structured prediction via the extra gradient method. In Proc. Advances in Neural Information Processing Systems Conference (NIPS). 2005: 1345-1352.

[97] Ratliff N, Bagnell J A, Zinkevich M. Subgradient methods for maximum margin structured learning. In Proc. ICML Workshop on Learning in Structured Output Spaces. 2006, 46.

[98] Desai C, Ramanan D, Fowlkes C C. Discriminative models for multi-class object layout [J]. International Journal of Computer Vision, 2011, 95(1): 1-12.

[99] Shen J, Liu G, Chen J, et al. Unified structured learning for simultaneous human pose estimation and garment attribute classification. IEEE Transactions on Image Processing, 2014, 23(11): 4786-4798.

[100] Lou X, Hamprecht F. Structured learning from partial annotations. arXiv preprint arXiv:1206.6421, 2012.

[101] Domke J. Structured learning via logistic regression. In Proc. Advances in Neural Information Processing Systems (NIPS). 2013: 647-655.

[102] Tsamardinos I, Brown L E, Aliferis C F. The max-min hill-climbing Bayesian network structure learning algorithm. Machine Learning, 2006, 65(1): 31-78.

[103] Pinto P C, Nagele A, Dejori M, et al. Using a local discovery ant algorithm for Bayesian network structure learning. Evolutionary Computation, IEEE Transactions on, 2009, 13(4): 767-779.

[104] Heckerman D, Geiger D, Chickering D M. Learning Bayesian networks: The combination of knowledge and statistical data. Machine Learning, 1995, 20(3): 197-243.

[105] Eaton D, Murphy K. Bayesian structure learning using dynamic programming and MCMC. arXiv preprint arXiv:1206.5247, 2012.

[106] De Campos C P, Ji Q. Efficient structure learning of Bayesian networks using constraints. The Journal of Machine Learning Research, 2011, 12: 663-689.

[107] Teyssier M, Koller D. Ordering-based search: A simple and effective algorithm for learning Bayesian networks. arXiv preprint arXiv:1207.1429, 2012.

[108] Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Alex Graves, Ioannis Antonoglou, Daan Wierstra, Martin A. Riedmiller: Playing Atari with Deep Reinforcement Learning. NIPS Workshop 2013.

[109] Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Andrei A. Rusu, Joel Veness, et al: Human-Level Control through Deep Reinforcement Learning. Nature 518(7540): 529-533 (2015).

[110] Junhyuk Oh, Valliappa Chockalingam, Satinder P. Singh, Honglak Lee: Control of Memory, Active Perception, and Action in Minecraft. International Conference on Machine Learning (ICML) 2016: 2790-2799.

[111] David Silver, Aja Huang, Chris J. Maddison, Arthur Guez, Laurent Sifre, et al: Mastering The Game of Go with Deep Neural Networks and Tree Search. Nature 529(7587): 484 – 489 (2016).

[113] Yang Gao, Yan Chen, K. J. Ray Liu: On Cost-Effective Incentive Mechanisms in Microtask Crowdsourcing. IEEE Trans. Comput. Intellig. and AI in Games 7(1): 3-15 (2015).

[117] Francisco S. Melo, M. Isabel Ribeiro: Emerging Coordination in Infinite Team Markov Games. AAMAS (1) 2008: 355-362.

[118] Yujing Hu, Yang Gao, Bo An: Accelerating Multiagent Reinforcement Learning by Equilibrium Transfer. IEEE T. Cybernetics 45(7): 1289-1302 (2015).

[119] Yujing Hu, Yang Gao, Bo An: Learning in Multi-agent Systems with Sparse Interactions by Knowledge Transfer and Game Abstraction. AAMAS 2015: 753-761.

[120] Xingguo Chen, Yang Gao, Ruili Wang: Online Selective Kernel-Based Temporal Difference Learning. IEEE Trans. Neural Netw. Learning Syst. 24(12): 1944-1956 (2013).

[121] Shangdong Yang, Yang Gao, Bo An, Hao Wang, Xingguo Chen: Efficient Average Reward Reinforcement Learning Using Constant Shifting Values. AAAI 2016: 2258-2264.

[122] Qingyu Guo, Bo An, Yevgeniy Vorobeychik, Long Tran-Thanh, Jiarui Gan, Chunyan Miao. Coalitional Security Games. AAMAS 2016: 159-167.

[123] Yue Yin, Haifeng Xu, Jiarui Gan, Bo An, Albert Jiang. Computing Optimal Mixed Strategies for Security Games with Dynamic Payoffs. IJCAI 2015: 681-688.

[124] Jiarui Gan, Bo An, Yevgeniy Vorobeychik. Security Games with Protection Externalities. AAAI 2015: 914-920.

[125] Yujing Hu, Yang Gao, Bo An: Multiagent Reinforcement Learning With Unshared Value Functions. IEEE T. Cybernetics 45(4): 647-662 (2015).

[126] Jinhua Song, Yang Gao, Hao Wang, Bo An: Measuring the Distance Between Finite Markov Decision Processes. AAMAS 2016: 468-476.

[127] Yu Y, Wang C, Gao Y, et al. A coupled clustering approach for items recommendation[C]//Pacific-Asia Conference on Knowledge Discovery and Data Mining. Springer, Berlin, Heidelberg, 2013: 365-376.

[128] Jian Y, David Z, Frangi A F, et al. Two-dimensional PCA: a new approach to appearance-based face representation and recognition. [J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2004, 26(1):131-137.

[129] Deng Cai, Chiyuan Zhang, Xiaofei He, Unsupervised Feature Selection for Multi-Cluster Data, 16th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD'10), July 2010.

[130] Xiaofei He, Deng Cai, and Partha Niyogi, Laplacian Score for Feature Selection, Advances in Neural Information Processing Systems 18 (NIPS'05), Vancouver, Canada, 2005

[131] Wright J, Ma Y, Mairal J, et al. Sparse representation for computer vision and pattern recognition[J]. Proceedings of the IEEE, 2010, 98(6): 1031-1044.

[132] W. Wang and Z.-H. Zhou. A new analysis of co-training. In Proc. of the 27th International Conference on Machine Learning (ICML), 1135-1142, 2010.

[133] Wanqi Yang, Yang Gao, Yinghuan Shi and Longbing Cao, “MRM-Lasso: A Sparse Multi-View Feature Selection Method via Low-Rank Analysis,” in IEEE Trans. on Neural Networks and Learning Systems (TNNLS), 2015, 26(11): 2801- 2815.

[134] Jing Huo, Yang Gao, Yinghuan Shi, Wanqi Yang, Hujun Yin. Ensemble of Sparse Cross-Modal Metrics for Heterogeneous Face Recognition. ACM Multimedia, 2016.

[135] Jing Huo, Yang Gao, Yinghuan Shi, Wanqi Yang, Hujun Yin. Heterogeneous Face Recognition by Margin Based Cross-Modality Metric Learning IEEE Trans. on Cybernetics (TCYB), 2017.

[136] Huang G, Liu Z, Weinberger K Q, et al. Densely connected convolutional networks[J]. arXiv preprint arXiv:1608.06993, 2016.

[137] Yang Z, Cohen W W, Salakhutdinov R. Revisiting semi-supervised learning with graph embeddings[J]. arXiv preprint arXiv:1603.08861, 2016.

[138] Kipf T N, Welling M. Semi-supervised classification with graph convolutional networks[J]. arXiv preprint arXiv:1609.02907, 2016.

[139] Frieze A, Kannan R, Vempala S. Fast Monte-Carlo algorithms for finding low-rank approximations. Journal of the ACM (JACM), 2004, 51(6): 1025-1041.

[140] Deshpande A, Rademacher L, Vempala S, et al. Matrix approximation and projective clustering via volume sampling. Proceedings of the seventeenth annual ACM-SIAM symposium on Discrete algorithm. Society for Industrial and Applied Mathematics, 2006: 1117-1126.

[141] Drineas P, Mahoney M W, Muthukrishnan S. Relative-error CUR matrix decompositions. SIAM Journal on Matrix Analysis and Applications, 2008, 30(2): 844-881.

[142] Boutsidis C, Drineas P, Magdon-Ismail M. Near-optimal column-based matrix reconstruction. SIAM Journal on Computing, 2014, 43(2): 687-717.

[143] Wang S, Zhang Z. Improving CUR matrix decomposition and the Nyström approximation via adaptive sampling. The Journal of Machine Learning Research, 2013, 14(1): 2729-2769.

[144] Yang T, Li Y F, Mahdavi M, et al. Nyström method vs random Fourier features: A theoretical and empirical comparison. Advances in neural information processing systems. 2012: 476-484.

[145] Guruswami V, Sinop A K. Optimal column-based low-rank matrix reconstruction. The 23rd Annual ACM-SIAM Symposium on Discrete Algorithms. SIAM, 2012: 1207-1214.

[146] Cao L. Non-IIDness Learning in Behavioral and Social Data [J]. The Computer Journal, 2014, 57(9): 1358–1370.

[147] Cao L. Coupling Learning of Complex Interactions [J]. Journal of Information Processing and Management, 2015, 51(9): 167–186.

[148] Steinwart I, Hush D, Scovel C. Learning from dependent observations [J]. Journal of Multivariate Analysis, Elsevier Inc., 2009, 100(1): 175–194.

[149] Mohri M, Rostamizadeh A. Stability bounds for non-iid processes [C]//Advances in Neural Information Processing. 2008, 11: 1025--1032.

[150] Ralaivola L, Szafranski M, Stempfel G. Chromatic PAC-Bayes Bounds for Non-IID Data: Applications to Ranking and Stationary β-Mixing Processes[J]. Journal of Machine Learning Research, 2009, 11(1999): 1927–1956.

[151] Steinwart I, Christmann A. Fast Learning from Non-i.i.d. Observations [C]//Advances in Neural Information Processing Systems. 2009, 22: 1–9.

[152] Wang C, Cao L, Wang M等. Coupled Nominal Similarity in Unsupervised Learning [C]//CIKM. ACM Press, 2011: 973–979.

[153] Wang C, Dong X, Zhou F等. Coupled Attribute Similarity Learning on Categorical Data [J]. IEEE Transactions on Neural Networks and Learning Systems, 2015, 26(4): 781–797.

[154] Wang C, She Z, Cao L. Coupled Attribute Analysis on Numerical Data[C]// International Joint Conference on Artificial Intelligence. 2013: 1736–1742.

[155] Jian S, Cao L, Pang G 等. Coupled Attribute Analysis on Numerical Data[C]// International Joint Conference on Artificial Intelligence. 2017.

[156] Liu C, Cao L. A Coupled k-Nearest Neighbor Algorithm for Multi-label Classification [C]// The Pacific-Asia Conference on Knowledge Discovery and Data Mining. 2015: 176–187.

[157] Li F, Xu G, Cao L. Coupled Matrix Factorization within Non-IID Context [C]// The Pacific-Asia Conference on Knowledge Discovery and Data Mining. 2015: 707–719.

[158] Cao L, Ou Y, Yu P等. Detecting Abnormal Coupled Sequences and Sequence Changes in Group-based Manipulative Trading Behaviors [C]// Proceedings of the 16th ACM SIGKDD international conference on Knowledge discovery and data mining. 2010: 85–94.

[159] Song Y, Cao L, Wu X等. Coupled Behavior Analysis for Capturing Coupling Relationships in Group-based Market Manipulation [C]// Proceedings of the 18th ACM SIGKDD international conference on Knowledge discovery and data mining. 2012: 976–984.

[160] Cao W, Hu L, Cao L等. Deep Modeling Complex Couplings within Financial Markets [C]// The AAAI Conference on Artificial Intelligence. 2015: 2518–2524.

[161] Xu Z, Zhang Y, Cao L. Social Image Analysis from a Non-IID Perspective [J]. IEEE Transactions on Multimedia, 2014, 16(7): 1986–1998.

[162] Shi Y, Suk H, Gao Y等. Joint Coupled-Feature Representation and Coupled Boosting for Alzheimer's Disease Diagnosis [C]// Conference on Computer Vision and Pattern Recognition. 2014: 2721-2728.

[163] Fan X, Cao L, Xu R. Dynamic Infinite Mixed-Membership Stochastic Blockmodel [J]. IEEE Transactions on Neural Networks and Learning Systems, 2015, 26(9): 2072–2085.

[164] Fan X, Xu R, Cao L. Copula Mixed-Membership Stochastic Blockmodel [C]// International Joint Conference on Artificial Intelligence. 2016: 1462–1468.

[165] Fan X, Xu R, Cao L 等. Learning Nonparametric Relational Models by Conjugately Incorporating Node Information in a Network [J]. IEEE transactions on cybernetics, 2017, 47(3): 589–599.

[166] Pang G, Cao L, Chen L. Outlier detection in complex categorical data by modelling the feature value couplings [C]// International Joint Conference on Artificial Intelligence. 2016: 1902–1908.

[167] Pang G, Cao L, Chen L. Unsupervised Feature Selection for Outlier Detection by Modelling Hierarchical Value-Feature Couplings. [C]// IEEE International Conference on Data Mining. 2016: 410–419.

[168] Pang G, Cao L, Chen L. Modeling Homophily Couplings for Wrapper-based Noise-resilient Outlier Detection. [C]// International Joint Conference on Artificial Intelligence. 2017.

[169] Cao L. Non-IID Recommender Systems: A Review and Framework of Recommendation Paradigm Shifting [J]. Engineering, 2016, 2(2): 212-224.

[170] Cao L, Yu P. Non-IID Recommendation Theories and Systems [J]. IEEE Intelligent Systems, 2016, 31(2): 81-84.

[171] Cao, L., Ou, Y. Yu, P. Coupled Behavior Analysis with Applications [J]. IEEE Trans. on Knowledge and Data Engineering, 24(8): 1378-1392 (2012).

[172] Cao, L. Combined Mining: Analyzing Object and Pattern Relations for Discovering and Constructing Complex but Actionable Patterns, WIREs Data Mining and Knowledge Discovery, 3(2): 140-155, 2013

[173] Cheng, X., Miao, D, Wang, C., Cao, L. Coupled Term-Term Relation Analysis for Document Clustering, IJCNN2013.

[174] Chen, Q., Hu, L., Xu, J., Liu, W., Cao, L. Document similarity analysis via involving both explicit and implicit semantic couplings. DSAA 2015: 1-10.

[175] Meng, X., Cao, L. and Shao, J. Semantic Approximate Keyword Query Based on Keyword and Query Coupling Relationship Analysis. CIKM 2014: 529-538.

[176] Meng, X., Cao, L. Zhang, X. and Shao, J. Top-k coupled keyword recommendation for relational keyword queries. Knowl. Inf. Syst. 50(3): 883-916 (2017)

[177] Shi, Y., Li, W., Gao, Y., Cao, L., Shen, D. Beyond IID: Learning to Combine Non-IID Metrics for Vision Tasks. AAAI2017.

中国计算机学会

微信号：ccfvoice