Dense Associative Memory Is Robust to Adversarial Inputs

Dense Associative Memory Is Robust to Adversarial Inputs

https://github.com/DimaKrotov/Dense_Associative_Memory/blob/master/Dense_Associative_Memory_training.ipynb

Abstract

Deep neural networks (DNNs) trained in a supervised way suffer from two known problems. First, the minima of the objective function used in learning correspond to data points (also known as rubbish examples or fooling images) that lack semantic similarity with the training data. Second, a clean input can be changed by a small, and often imperceptible for human vision, perturbation so that the resulting deformed input is misclassified by the network. These findings emphasize the differences between the ways DNNs and humans classify patterns and raise a question of designing learning algorithms that more accurately mimic human perception compared to the existing methods.

Our article examines these questions within the framework of dense associative memory (DAM) models. These models are defined by the energy function, with higher-order (higher than quadratic) interactions between the neurons. We show that in the limit when the power of the interaction vertex in the energy function is sufficiently large, these models have the following three properties. First, the minima of the objective function are free from rubbish images, so that each minimum is a semantically meaningful pattern. Second, artificial patterns poised precisely at the decision boundary look ambiguous to human subjects and share aspects of both classes that are separated by that decision boundary. Third, adversarial images constructed by models with small power of the interaction vertex, which are equivalent to DNN with rectified linear units, fail to transfer to and fool the models with higher-order interactions. This opens up the possibility of using higher-order models for detecting and stopping malicious adversarial attacks. The results we present suggest that DAMs with higher-order energy functions are more robust to adversarial and rubbish inputs than DNNs with rectified linear units.

1  Introduction

In a recent paper Krotov and Hopfield (2016) proposed that dense associative memory (DAM) models with higher-order interactions in the energy function learn representations of the data, which strongly depend on the power of the interaction vertex. The network extracts features from the data for small values of this power, but as the power of the interaction vertex is increased, there is a gradual shift to a prototype-based representation, the two extreme regimes of pattern recognition known in cognitive psychology. Remarkably, there is a broad range of powers of the energy function, for which the representation of the data is already in the prototype regime, but the accuracy of classification is still competitive with the best available algorithms (based on DNN with rectified linear units, ReLUs). This suggests that the DAM models might behave very differently compared to the standard methods used in deep learning with respect to adversarial deformations.

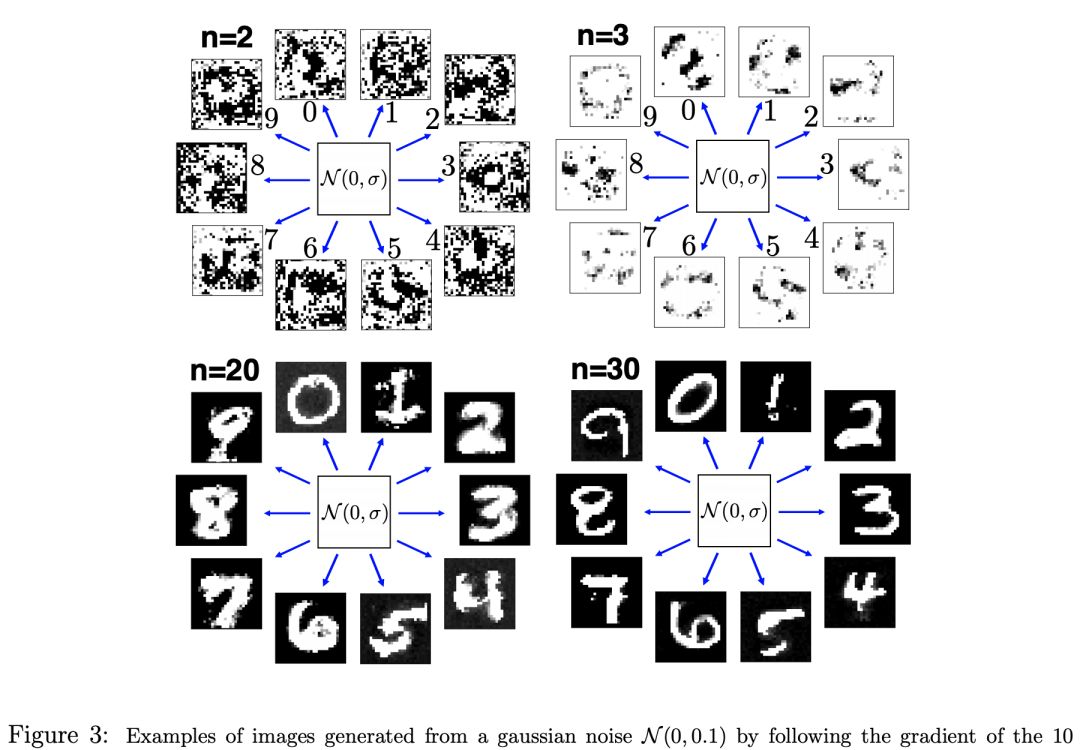
In this article, we report three main results. First, using gradient descent in the pixel space, a set of “rubbish” images is constructed that correspond to the minima of the objective function used in training. This is done on the MNIST data set of handwritten digits using different values of the power of the interaction vertex, which is denoted by  n n . For small values of the power  n n , these images indeed look like speckled rubbish noise and do not have any semantic content for human vision, a result consistent with (Nguyen et al., 2015). However, as the power of the interaction vertex is increased, the images gradually become less speckled and more semantically meaningful. In the limit of very large  n≈20,…,30 n ≈ 20 , … , 30 , these images are no longer rubbish at all. They represent plausible images of handwritten digits that could possibly have been produced by a human. Second, starting from clean images from the data set, a set of adversarial images is constructed in such a way that each image is placed exactly on the decision boundary between two label classes. For small powers  n n , these images look very similar to the initial clean image with a little bit of speckled noise added, but they are misclassified by the neural network, a result consistent with Szegedy et al. (2013). However, as the power of the interaction vertex is increased, these adversarial images become less and less similar to the initial clean image. In the limit of very large powers, these adversarial images look either like a morphed image of two digits (the initial clean image and another digit from the class that the deformation targets) or the initial digit superimposed on a ghost image from the target class. Either way, the interpretation of the artificial patterns generated by the neural net on the decision boundary requires the presence of another digit from the target class in addition to the initial seed from the data set and cannot be explained by simply adding noise to the initial clean image. Third, adversarial and rubbish images generated by models with small  n n  can be transferred to and fool another model with a small (but possibly different) value  n n . However, they fail to transfer to models with large  n n . Thus, rubbish and adversarial images generated by models with small  n n  cannot fool models with large  n n . In contrast, the “rubbish” images generated by models with large  n n  can be transferred to models with small  n n , but this is not a problem since those “rubbish” images are actually not rubbish at all and look like credible handwritten digits. These results suggest that the DAMs with a large power of the interaction vertex in the energy function better mimic the psychology of human visual perception than DAMs with a small power (at least on a simple MNIST data set). The latter are equivalent to DNNs with ReLUs (Krotov & Hopfield, 2016).

7  Discussion and Conclusion

Although modern machine learning techniques outperform humans on many classification tasks, there is a serious concern that they do not understand the structure of the training data. A clear demonstration of this lack of understanding was presented in Szegedy et al. (2013) and Nguyen et al. (2015), which showed two examples of nonsensical predictions of DNNs that contradict human visual perception: adversarial images and rubbish images. In this article, we propose that DAMs with higher-order interactions in the energy function produce more sensible interpretations (consistent with human vision) of adversarial and rubbish images on MNIST. We argue that these models better mimic human visual perception than DNNs with ReLUs.

A possible explanation of adversarial examples, pertaining to neural networks being too linear, was given in Goodfellow et al. (2014). Our explanation follows the same line of thought with some differences. One result of Krotov and Hopfield (2016) is that DAMs with large powers of the interaction vertex in the energy function are dual to feedforward neural nets with highly nonlinear activation functions—the rectified polynomials of higher degrees. From the perspective of this duality, one might expect that by simply replacing the ReLUs in DNNs by the higher rectified polynomials, one might solve the problem of adversarial and rubbish images for a sufficiently large power of the activation function. We tried that and discovered that although DNNs with higher rectified polynomials alone perform better than DNNs with ReLUs from the adversarial perspective, they are worse than DAMs with the update rule, equation 2.1. These observations need further comprehensive investigation. Thus, simply changing ReLUs to higher rectified polynomials is not enough to get rid of adversarial problems, and other aspects of the training algorithm presented in section 2 are important.

For all values of  n n  studied in this article, the classification decision is made based on the votes of both feature and prototype detectors. These votes are “undemocratic,” so that the larger  n n  is, the stronger the prototype votes are. In the extreme limit  n→∞ n → ∞ , DAM reduces to the nearest-neighbor classifier. In this regime, DAMs are somewhat similar to RBF networks in which the hidden units compute a gaussian weight around a set of memorized templates. RBF networks are resistant to adversarial examples (Goodfellow et al., 2014) but are poor at generalization, as are DAMs at  n→∞ n → ∞ . In a sense, the contribution of this study is the identification of a strength of nonlinearity of the neural networks (power  n n ) for which the generalization ability is still strong but the adversarial problems are already sufficiently mitigated. In all four models that we have discussed, the power  n n  is chosen in such a way that features cooperate with prototypes to have a good generalization performance. Thus, it is important to keep  n n large but finite, so that DAMs are not in the pure RBF regime.

There are two straightforward ideas for possible extensions of this work. First, it would be interesting to complement the proposed training procedure with adversarial training—in other words, to train the large  n n  networks using the algorithm of section 2but on a combination of clean images and adversarial images, along the lines of Goodfellow et al. (2014) and Nøkland (2015). We expect that this should further increase the robustness to adversarial examples and increase the classification accuracy on the clean images. Second, it would be interesting to investigate the proposed methods in the convolutional setting. Naively, one expects that the adversarial problems are more severe in the fully connected networks than in the convolutional networks. For this reason, we used the fully connected networks for our experiments. We expect that the training algorithm of section 2 can be combined with convolutional layers to better describe images.

Although more work is required to fully resolve the problem of adversarial and rubbish images, we believe that this article has identified a promising computational regime that significantly mitigates the vulnerability of neural networks to adversarial and rubbish images and that remains little investigated.

参考：

https://arxiv.org/pdf/1701.00939.pdf

https://github.com/DimaKrotov/Dense_Associative_Memory/blob/master/Dense_Associative_Memory_training.ipynb