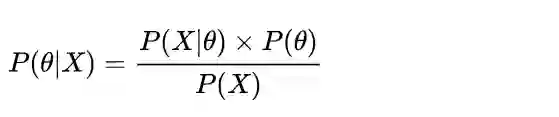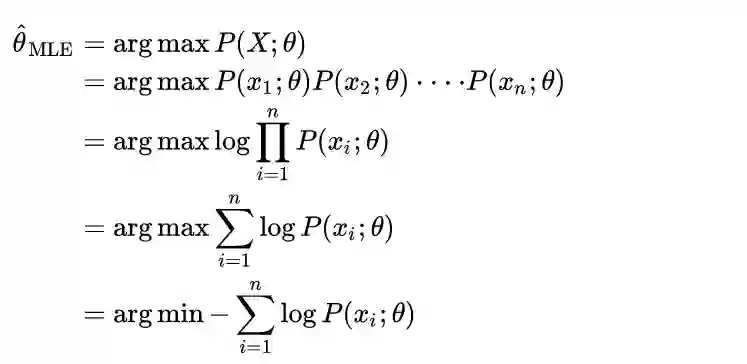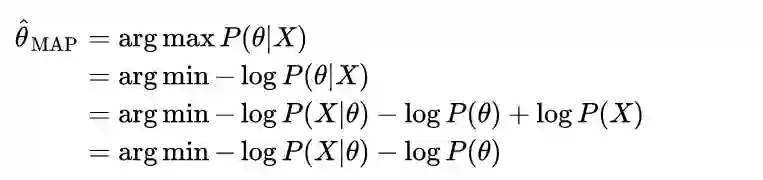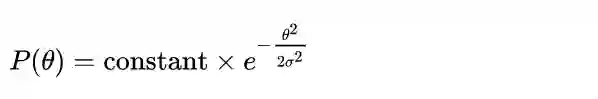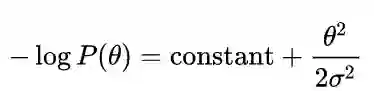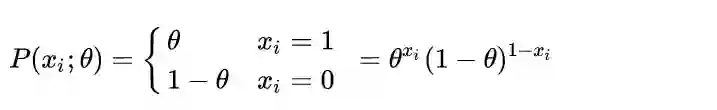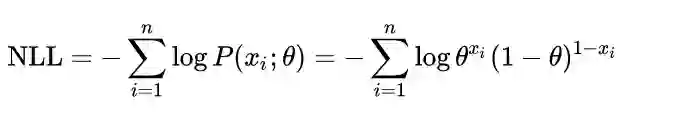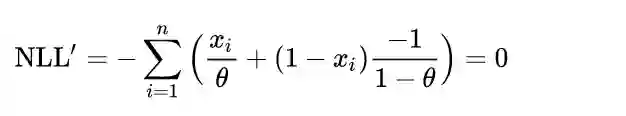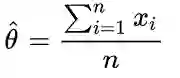频率学派还是贝叶斯学派？聊一聊机器学习中的MLE和MAP

作者：夏飞
Google | 软件工程师
量子位 已获授权编辑发布
转载请联系原作者

本文作者夏飞，清华大学计算机软件学士，卡内基梅隆大学人工智能硕士，现为谷歌软件工程师。

在这篇文章中，他探讨了机器学习中的MLE和MAP两大学派的争论。

• 频率学派 - Frequentist - Maximum Likelihood Estimation (MLE，最大似然估计)

• 贝叶斯学派 - Bayesian - Maximum A Posteriori (MAP，最大后验估计)

概述

有时候和别人聊天，对方会说自己有很多机器学习经验，深入一聊发现，对方竟然对MLE和MAP一知半解，至少在我看来，这位同学的机器学习基础并不扎实。难道在这个深度学习盛行的年代，不少同学都只注重调参数？

现代机器学习的终极问题都会转化为解目标函数的优化问题，MLE和MAP是生成这个函数的很基本的思想，因此我们对二者的认知是非常重要的。这次就和大家认真聊一聊MLE和MAP这两种estimator。

两大学派的争论

抽象一点来讲，频率学派和贝叶斯学派对世界的认知有本质不同：频率学派认为世界是确定的，有一个本体，这个本体的真值是不变的，我们的目标就是要找到这个真值或真值所在的范围；而贝叶斯学派认为世界是不确定的，人们对世界先有一个预判，而后通过观测数据对这个预判做调整，我们的目标是要找到最优的描述这个世界的概率分布。

在对事物建模时，用θ表示模型的参数，请注意，解决问题的本质就是求θ。那么：

(1) 频率学派：存在唯一真值θ。举一个简单直观的例子—抛硬币，我们用P(head)来表示硬币的bias。抛一枚硬币100次，有20次正面朝上，要估计抛硬币正面朝上的bias P(head)=θ。在频率学派来看，θ= 20 / 100 = 0.2，很直观。

当数据量趋于无穷时，这种方法能给出精准的估计；然而缺乏数据时则可能产生严重的偏差。例如，对于一枚均匀硬币，即θ= 0.5，抛掷5次，出现5次正面 (这种情况出现的概率是1/2^5=3.125%)，频率学派会直接估计这枚硬币θ= 1，出现严重错误。

(2) 贝叶斯学派： θ是一个随机变量，符合一定的概率分布。在贝叶斯学派里有两大输入和一大输出，输入是先验 (prior)和似然 (likelihood)，输出是后验 (posterior)。

先验，即P(θ)，指的是在没有观测到任何数据时对θ的预先判断，例如给我一个硬币，一种可行的先验是认为这个硬币有很大的概率是均匀的，有较小的概率是是不均匀的；似然，即P(X|θ)，是假设θ已知后我们观察到的数据应该是什么样子的；后验，即P(θ|X)，是最终的参数分布。

贝叶斯估计的基础是贝叶斯公式，如下：

同样是抛硬币的例子，对一枚均匀硬币抛5次得到5次正面，如果先验认为大概率下这个硬币是均匀的 (例如最大值取在0.5处的Beta分布)，那么P(head)，即P(θ|X)，是一个distribution，最大值会介于0.5~1之间，而不是武断的θ= 1。

这里有两点值得注意的地方：

随着数据量的增加，参数分布会越来越向数据靠拢，先验的影响力会越来越小

如果先验是uniform distribution，则贝叶斯方法等价于频率方法。因为直观上来讲，先验是uniform distribution本质上表示对事物没有任何预判。

MLE - 最大似然估计

Maximum Likelihood Estimation, MLE是频率学派常用的估计方法！

假设数据X₁，X₂，…，X_n是i.i.d.的一组抽样，X=(X₁，X₂，…，X_n)。其中i.i.d.表示Independent and identical distribution，独立同分布。那么MLE对θ的估计方法可以如下推导：

最后这一行所优化的函数被称为Negative Log Likelihood (NLL)，这个概念和上面的推导是非常重要的！

我们经常在不经意间使用MLE，例如

上文中关于频率学派求硬币概率的例子，其方法其实本质是由优化NLL得出。本文末尾附录中给出了具体的原因 :-)

给定一些数据，求对应的高斯分布时，我们经常会算这些数据点的均值和方差然后带入到高斯分布的公式，其理论依据是优化NLL

深度学习做分类任务时所用的cross entropy loss，其本质也是MLE

MAP - 最大后验估计

Maximum A Posteriori, MAP是贝叶斯学派常用的估计方法！

同样的，假设数据X₁，X₂，…，X_n是i.i.d.的一组抽样，X=(X₁，X₂，…，X_n) 。那么MAP对θ的估计方法可以如下推导：

其中，第二行到第三行使用了贝叶斯定理，第三行到第四行P(X)可以丢掉因为与θ无关。注意-log P(X|θ)其实就是NLL，所以MLE和MAP在优化时的不同就是在于先验项-log P(θ)。好的，那现在我们来研究一下这个先验项，假定先验是一个高斯分布，即

那么，

。至此，一件神奇的事情发生了 — 在MAP中使用一个高斯分布的先验等价于在MLE中采用L2的regularizaton !

再稍微补充几点：

我们不少同学大学里学习概率论时，最主要的还是频率学派的思想，其实贝叶斯学派思想也非常流行，而且实战性很强

CMU的很多老师都喜欢用贝叶斯思想解决问题；我本科时的导师朱军老师也在做贝叶斯深度学习的工作，有兴趣可以关注一下。

相关研究论文：

https://arxiv.org/abs/1709.05870

后记

有的同学说：“了解这些没用，现在大家都不用了。”这种想法是不对的，因为这是大家常年在用的知识，是推导优化函数的核心，而优化函数又是机器学习 (包含深度学习) 的核心之一。这位同学有这样的看法，说明对机器学习的本质并没有足够的认识，而让我吃惊的是，竟然有不少其他同学为这种看法点赞。内心感到有点儿悲凉，也引发了我写这篇文章的动力，希望能帮到一些朋友 :-)

参考资料

[1] Bayesian Method Lecture, UT Dallas.
http://www.utdallas.edu/~nrr150130/cs7301/2016fa/lects/Lecture_14_Bayes.pdf

[2] MLE, MAP, Bayes classification Lecture, CMU.
http://www.cs.cmu.edu/~aarti/Class/10701_Spring14/slides/MLE_MAP_Part1.pdf

附录

为什么说频率学派求硬币概率的算法本质是在优化NLL？

因为抛硬币可以表示为参数为θ的Bernoulli分布，即：

其中x_i= 1 表示第i次抛出正面。那么，

求导数并使其等于零，得到


即

，也就是出现正面的次数除以总共的抛掷次数。

点击左下角“阅读原文”，可解锁更多作者的文章

还可以直接参与讨论~

量子位特约稿件，转载请联系原作者。

— 完 —

加入社群

量子位AI社群13群开始招募啦，欢迎对AI感兴趣的同学，加小助手微信qbitbot5入群；

此外，量子位专业细分群(自动驾驶、CV、NLP、机器学习等)正在招募，面向正在从事相关领域的工程师及研究人员。

进群请加小助手微信号qbitbot5，并务必备注相应群的关键词~通过审核后我们将邀请进群。（专业群审核较严，敬请谅解）

诚挚招聘

量子位正在招募编辑/记者，工作地点在北京中关村。期待有才气、有热情的同学加入我们！相关细节，请在量子位公众号(QbitAI)对话界面，回复“招聘”两个字。

量子位 QbitAI · 头条号签约作者

վ'ᴗ' ի 追踪AI技术和产品新动态