QA派|初识GraphSAGE

文 · 成森      封面 · pixabay

QA派|初识GraphSAGE

图网络中节点的低维embedding，对于各类预测、图分析任务都非常有用；相对于要求一整张图作为输入的GCN，能分批训练的GraphSAGE在工业界似乎更加常用。本文通过问答的形式，来对GraphSAGE有个初步全面的了解。

QA派，用问答的形式为加深对模型、问题的理解，同时也有助于不断深入。

目录

• 基本概念

• 有了GCN为啥还要GraphSAGE？

• GraphSAGE有什么优点？

• GraphSAGE的基本思路是什么？

• 跳数（hops）、搜索深度（search depth）、阶数（order）有啥区别？

• 采样

• 为什么要采样？

• 采样数大于邻接节点数怎么办？

• 采样的邻居节点数应该选取多大？

• 每一跳采样需要一样吗？

• 适合有向边吗？

• 采样是随机的吗？

• 聚合函数

• 聚合函数的选取有什么要求？

• GraphSAGE论文中提供多少种聚合函数？

• 均值聚合的操作是怎样的？

• pooling聚合的操作是怎样的？

• 使用LSTM聚合时需要注意什么？

• 均值聚合和其他聚合函数有啥区别？

• max-和mean-pooling有什么区别？

• 这三种聚合方法，哪种比较好？

• 一般聚合多少层？层数越多越好吗？

• 什么时候和GCN的聚合形式“等价”？

• 无监督学习

• GraphSAGE怎样进行无监督学习？

• GraphSAGE如何定义邻近和远处的节点？

• 如何计算无监督GraphSAGE的损失函数？

• GraphSAGE是怎么随机游走的？

• GraphSAGE什么时候考虑边的权重了？

• 训练

• 如果只有图、没有节点特征，能否使用GraphSAGE？

• 训练好的GraphSAGE如何得到节点Embedding？

• minibatch的子图是怎么得到的？

• 增加了新的节点来训练，需要为所有“旧”节点重新输出embeding吗？

• GraphSAGE有监督学习有什么不一样的地方吗？

• 对比

• 那和DeepWalk、Node2vec这些有什么不一样？

基本概念

有了GCN为啥还要GraphSAGE？

GCN灵活性差、为新节点产生embedding要求 额外的操作 ，比如“对齐”：

• GCN是  直推式（transductive） 学习，无法直接泛化到新加入（未见过）的节点；
• GraphSAGE是  归纳式（inductive） 学习，可以为新节点输出节点特征。

GCN输出固定：

• GCN输出的是节点 唯一确定 的embedding；
• GraphSAGE学习的是节点和邻接节点之间的关系，学习到的是一种 映射关系 ，节点的embedding可以随着其邻接节点的变化而变化。

GCN很难应用在超大图上：

• 无论是拉普拉斯计算还是图卷积过程，因为GCN其需要对 整张图 进行计算，所以计算量会随着节点数的增加而递增。
• GraphSAGE通过采样，能够形成 minibatch 来进行批训练，能用在超大图上。

GraphSAGE有什么优点？

• 采用 归纳学习 的方式，学习邻居节点特征关系，得到泛化性更强的embedding；
• 采样技术，降低空间复杂度，便于构建minibatch用于 批训练 ，还让模型具有更好的泛化性；
• 多样的聚合函数 ，对于不同的数据集/场景可以选用不同的聚合方式，使得模型更加灵活。

GraphSAGE的基本思路是什么？

既然新增的节点，一定会改变原有节点的表示，那么为什么一定要得到每个节点的一个固定的表示呢？何不直接学习一种节点的表示方法呢？

为了回答上面的问题，GraphSAGE的基本思路是：利用一个 聚合函数 ，通过 采样 和学习聚合节点的局部邻居特征，来为节点产生embedding。

跳数（hops）、搜索深度（search depth）、阶数（order）有啥区别？

我们经常听到一阶邻居、二阶邻居，1-hops、2-hops等等，其实他们都是一个概念，就是该节点和目标节点的路径长度，如果路径长度是1，那就是一阶邻接节点、1-hops node。

搜索深度其实和深度搜索的深度的概念相似，也是用路径长度来衡量。

简单来说，这几个概念某种程度上是等价。

在GraphSAGE中，还有聚合层数\迭代次数，比如说只考虑了一阶邻接节点，那就只有一层聚合（迭代了一次），以此类推。

采样

为什么要采样？

出于对计算效率的考虑，对每个节点采样一定数量的邻接节点作为待聚合信息的节点。

从训练效率考虑：

• 通过采样，可以得到一个 固定大小 的领域集，可以拼成一个batch，送到GPU中进行批训练。

从复杂度角度考虑：

• 如果没有采样，单个batch的内存使用和预期运行时间是 不可预测 的；最坏的情况是 ，即所有的节点都是目标节点的邻接节点。
• 而GraphSAGE的每个batch的空间和时间复杂度都是 固定 的， ，其中K是指层数，也就是要考虑多少阶的邻接节点， 是在第i层采样的数量。

采样数大于邻接节点数怎么办？

设采样数量为n：

• 若节点邻居数少于n，则采用 有放回 的抽样方法，直到采样出K个节点。
• 若节点邻居数大于n，则采用 无放回 的抽样。

当然，若不考虑计算效率，我们完全可以对每个节点利用其所有的邻居节点进行信息聚合，这样是信息无损的。但这么做可能就没法使用批训练了。

采样的邻居节点数应该选取多大？

关于邻居的个数，文中提到 ，即两次扩展的邻居数之积小于500，大约每次只需要扩展20来个邻居时获得较高的性能。

实验中也有关于邻居采样数量的对比，如下图，随着邻居抽样数量的递增，边际效益递减，而且计算时间也会增大。

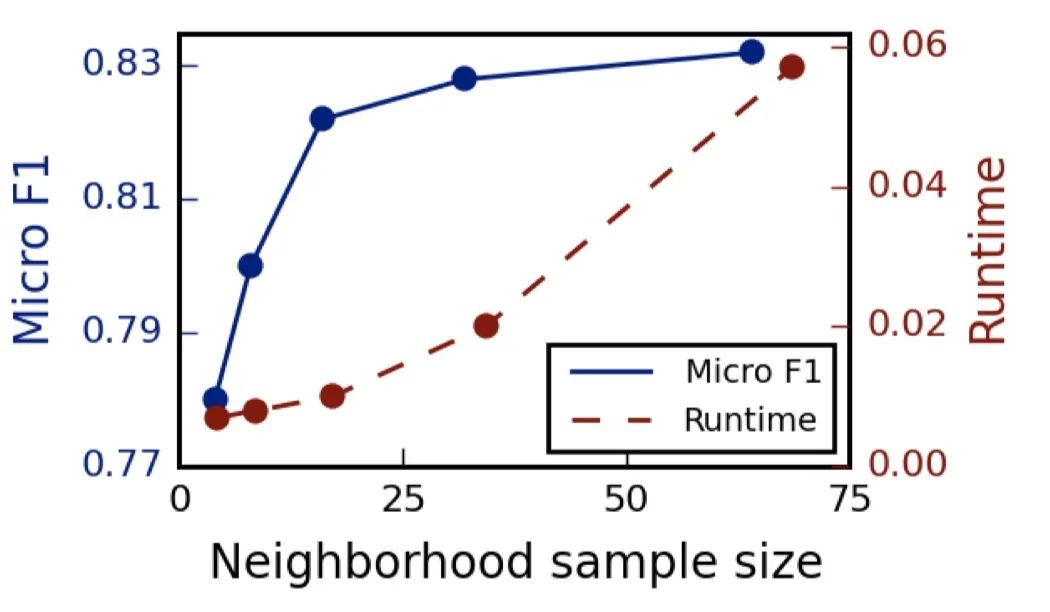
每一跳采样需要一样吗？

不需要，可以分别设置每一跳的采样数量，来进一步缓解因 阶数越高涉及到的节点越多 的问题。

原文中，一阶采样数是25，二阶采样数是10。这时候二阶的节点总数是250个节点，计算量大大增加。

适合有向边吗？

适合，只需要采样邻居节点时考虑边的方向即可。

采样是随机的吗？

原论文里使用的是uniform sampling，即均匀采样。

同时原文指出，探索非均匀采样是值得探索的方向（比如pinSAGE的重要性采样）。

聚合函数

聚合函数的选取有什么要求？

由于在图中节点的邻居是 天然无序 的，所以我们希望构造出的聚合函数是 对称 的（即改变输入的顺序，函数的输出结果不变），同时具有 较强的表达能力 （比如可以参数学习）。

GraphSAGE论文中提供多少种聚合函数？

原文中提供三种聚合函数：

• 均值聚合
• pooling聚合(max-pooling/mean-pooling)
• LSTM聚合

均值聚合的操作是怎样的？

1. 目标节点 和邻居节点
2. 把目标节点和邻居节点的特征 纵向拼接 起来 
3. 对拼接起来的向量进行 纵向均值化 操作 
4. 将得到的结果做一次 非线性变换 产生目标节点的向量表征。

pooling聚合的操作是怎样的？

1. 目标节点 和邻居节点
2. 先对邻接节点的特征向量进行一次非线性变换
3. 之后进行一次pooling操作(max-pooling or mean-pooling)
4. 将得到结果与第k-1层的目标节点的表示向量拼接
5. 最后再经过一次非线性变换得到目标节点的第k层表示向量。

使用LSTM聚合时需要注意什么？

复杂结构的LSTM相比简单的均值操作具有更强的表达能力，然而由于LSTM函数 不是关于输入对称 的，所以在使用时需要对节点的邻居进行 乱序操作 。

均值聚合和其他聚合函数有啥区别？

除了聚合方式，最大的区别在于均值聚合 没有拼接操作 （算法1的第五行），也就是均值聚合不需要把 当前节点上一层的表征 拼接到 已聚合的邻居表征上。

这一拼接操作可以简单看成不同“搜索深度”之间的“ skip connection ”（残差结构），并且能够提供显著的性能提升。

max-和mean-pooling有什么区别？

原文中提到，max-pooling和mean-pooling在测试中并没有明显的区别，所以原文主要使用max-pooling。

这三种聚合方法，哪种比较好？

如果按照其学习参数数量来看，LSTM > Pooling > 均值聚合。

而在实验中也发现，在Reddit数据集中，LSTM和max-pooling的效果确实比均值聚合要好一些。

一般聚合多少层？层数越多越好吗？

和GCN一样，一般只需要 1～2层 就能获得比较好的结果；如果聚合3层及以上，其时间复杂度也会随着层数的增加而大幅提升，而且效果并没有什么变化。

在GraphSAGE，两层比一层有10-15%的提升；但将层数设置超过2，边际效果上只有0-5%的提升，但是计算时间却变大了10-100倍。

什么时候和GCN的聚合形式“等价”？

聚合函数为 均值聚合 时，其聚合形式与GCN“近似等价”，也就是论文中提到的GraphSAGE-GCN。

无监督学习

GraphSAGE怎样进行无监督学习？

基本思想是：希望 邻近 的节点具有相似的向量表征，同时让 远处 的节点的表示尽可能区分。

通过负采样的方法，把邻近节点作为正样本，把远处节点作为负样本，使用类似word2vec的方法进行无监督训练。

GraphSAGE如何定义邻近和远处的节点？

从 节点u 出发，能够通过 随机游走 到达的节点，则是邻近节点v；其他则是远处节点 。

如何计算无监督GraphSAGE的损失函数？

其中：

• ：节点 是从节点 的负采样分布 采样的
• ：负采样的数量
• ：是当前节点； ：随机游走可到达的邻居； ：远处节点（负采样节点）
• ：GraphSAGE为该节点输出的embedding，和以前embedding方法不同的是， 是由节点及其局部邻居节点共同决定产生，而不是每个节点的唯一embedding（通过look-up表获得那种）
• embedding之间的相似度通过 向量点积 的方法计算得到（余弦相似度）。

至于为什么负采样的公式长成这样，建议阅读《 word2vec Explained: Deriving Mikolov et al.’s Negative-Sampling Word-Embedding Method 》

GraphSAGE是怎么随机游走的？

在原文中，为每个节点进行50次步长为5的随机游走，随机游走的实现方式是直接使用DeepWalk的Python代码。

至于具体的实现，可以针对数据集来设计你的随机游走算法，比如考虑了权重的有偏游走。

GraphSAGE什么时候考虑边的权重了？

类似的问题：GraphSAGE什么时候使用用了图信息？

• 在采样的时候。
• （带权）随机游走进行负采样的时候。

训练

如果只有图、没有节点特征，能否使用GraphSAGE？

原文里有一段描述：our approach can also make use of structural features that are present in all graphs (e.g., node degrees). Thus, our algorithm can also be applied to graphs without node features.

所以就节点没有特征，但也可以根据其结构信息为其构建特征，比如说节点的度数等等。

训练好的GraphSAGE如何得到节点Embedding？

假设GraphSAGE已经训练好，我们可以通过以下步骤来获得节点embedding，具体算法请看下图的算法1。

训练过程则只需要将其产生的embedding扔进损失函数计算并反向梯度传播即可。

• 对图中每个节点的邻接节点进行 采样 ，输入节点及其n阶邻接节点的特征向量
• 根据K层的 聚合函数 聚合邻接节点的信息
• 就产生了各节点的embedding

minibatch的子图是怎么得到的？

其实这部分看一下源码就容易理解了。下图的伪代码，核心步骤和算法1差不多，就是在其前向传播之前，多了个minibatch的操作。

• 先对所有需要计算的节点进行采样（算法2中的2～7行）。用一个字典来保存节点及其对应的邻接节点。

• 然后训练时随机挑选n个节点作为一个batch，然后通过字典找到对应的一阶节点，进而找到二阶甚至更高阶的节点。这样一阶节点就形成一个batch，K=2时就有三个batch。

• 抽样时的顺序是： ；训练时，使用迭代的方式来聚合，其顺序是： 。简单来说，从上到下采样，形成每一层的batch；每一次迭代都从下到上，计算k-1层batch来获得k层的节点embedding，如此类推。

• 每一个minibatch只考虑batch里的节点的计算，不在的不考虑，所以这也是节省计算方法。

• 在算法2的第3行中， ，也就是说采样邻居节点时，也考虑了自身节点的信息。相当于GCN中邻接矩阵增加单位矩阵。

增加了新的节点来训练，需要为所有“旧”节点重新输出embeding吗？

需要。因为GraphSAGE学习到的是节点间的关系，而增加了新节点的训练，这会使得关系参数发生变化，所以旧节点也需要重新输出embedding。

GraphSAGE有监督学习有什么不一样的地方吗？

没有。监督学习形式根据任务的不同，直接设置目标函数即可，如最常用的节点分类任务使用交叉熵损失函数。

对比

那和DeepWalk、Node2vec这些有什么不一样？

DeepWalk、Node2Vec这些embedding算法直接训练每个节点的embedding，本质上依然是直推式学习，而且需要大量的额外训练才能使他们能预测新的节点。同时，对于embedding的正交变换（orthogonal transformations），这些方法的目标函数是不变的，这意味着生成的向量空间在不同的图之间不是天然泛化的，在再次训练（re-training）时会产生漂移（drift）。

与DeepWalk不同的是，GraphSAGE是通过聚合节点的邻接节点特征产生embedding的，而不是简单的进行一个embedding lookup操作得到。