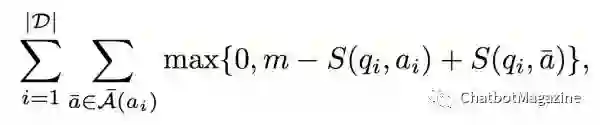揭开知识库问答KB-QA的面纱3·向量建模篇

作者丨刘大一恒

学校丨四川大学博士生

本期我们将介绍 KB-QA 传统方法之一的向量建模（Vector Modeling），我们以一个该方法的经典代表作为例，为大家进一步揭开知识库问答的面纱。该方法来自 Facebook 公司 Bordes A, Chopra S, Weston J 的论文 Question answering with subgraph embeddings（文章发表于 2014 年的 EMNLP 会议）。

1. 向量建模的核心思想

向量建模方法的思想和信息抽取的思想比较接近。首先根据问题中的主题词在知识库中确定候选答案。把问题和候选答案都映射到一个低维空间，得到它们的分布式表达（Distributed Embedding），通过训练数据对该分布式表达进行训练，使得问题向量和它对应的正确答案向量在低维空间的关联得分（通常以点乘为形式）尽量高。

当模型训练完成后，则可根据候选答案的向量表达和问题表达的得分进行筛选，找出得分最高的作为最终答案。 

此时，你的心中可能会出现两个问题，一是如何将问题和答案映射到低维空间，显然我们不能仅仅将自然语言的问题和答案进行映射，还要将知识库里的知识也映射到这个低维空间中（否则我们就只是在做 QA 而非 KB-QA 了）。

第二个问题是，如果做过类似工作（one-shot，imgae caption，word embedding 等）的朋友应该知道，使用这种方法是需要大量数据去训练这个低维空间的分布式表达的，而 KB-QA 中的 benchmark 数据集 WebQuestion 只含有 5800 多个问题答案对，这样的数据是难以训练好这种表达的。 

接下来，就让我们带着这两个问题，一起看看作者是怎么解决的。

2. 如何用分布式表达表示答案和问题

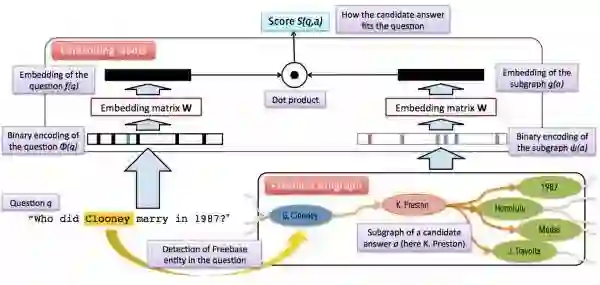
问题的分布式表达：首先我们把自然语言问题进行向量化，作者将输入空间的维度 N 设置为字典的大小+知识库实体数目+知识库实体关系数目，对于输入向量每一维的值设置为该维所代表的单词（当然这一维也可能代表的是某个实体数目或实体关系，对于问题的向量化，这些维数都设置为 0）在问题中出现的次数（一般为 0 或 1 次），可以看出这是一种 multi-hot 的稀疏表达，是一种简化版的词袋模型（Bag-of-words model）。 

我们用 q 代表问题，用 Φ(q) 代表 N 维的问题向量，用矩阵 W 将 N 维的问题向量映射到 k 维的低维空间，那么问题的分布式表达即 f(q)=WΦ(q)。

答案的分布式表达：我们想想可以怎样对答案进行向量化，最简单的方式，就是像对问题一样的向量化方式，使用一个简化版的词袋模型。由于答案都是一个知识库实体，那么这样的表达就是一个 one-hot 的表达，显然，这种方式并没有把知识库的知识引入到我们的输入空间中。 

第二种方式，我们把知识库想象成一个图，图的节点代表实体，边代表实体关系。通过问题中的主题词可以定位到图中的一个节点，该节点到答案节点有一条路径，我们把该路径上的所有边（实体关系）和点（实体）都以 multi-hot 的形式存下来作为答案的输入向量。

我们这里只考虑一跳（hop）或者两跳的路径，如路径（barack obama, place of birth, honolulu）是一跳，路径（barack obama, people.person.place of birth, location.location.containedby, hawaii）是两跳。因此这种表示是一种 3-hot 或 4-hot 的表示。 

第三种方式，让我们回想一下我们在揭开知识库问答KB-QA的面纱3·信息抽取篇介绍的信息抽取的方法，对于每一个候选答案，该答案所对应的属性（type/gender 等）和关系都是能够帮助我们判断它是否是正确答案的重要信息。

因此我们可以把每个候选答案对应的知识库子图（1 跳或 2 跳范围）也加入到输入向量中，假设该子图包含 C 个实体和 D 个关系，那么我们最终的表达是一种 3+C+D-hot 或者 4+C+D-hot 的表达。和信息抽取方法一样，我们也对关系的方向进行区分，因此我们输入向量的大小变为字典的大小+2*（知识库实体数目+知识库实体关系数目）。

同样的，我们用 a 表示答案，用 Ψ(a) 表示答案的输入向量，用矩阵 W 将问题向量映射到 k 维的低维空间，答案的分布式表达即 g(a)=WΨ(a)。

向量得分：最后我们用一个函数表征答案和问题的得分，我们希望问题和它对应的正确答案得尽量高分，通过比较每个候选答案的得分，选出最高的，作为正确答案。得分函数定义为二者分布式表达的点乘，即。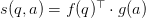

上述整个流程如下图所示：

3. 如何训练分布式表达

对于训练数据集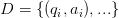，我们一个定义 margin-based ranking 损失函数，公式如下：

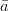
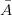
做过 zero-shot 或者对 SVM 了解的朋友应该对这个式子不会陌生，其中  表示负样本集  中的一个负样本（错误答案），m 是一个值为 0.1 的 margin。最小化这个损失函数，意味着我们希望正确答案和问题的得分要比任意错误答案的得分高出一个 margin。 

和训练 word embedding 一样，为减少计算量，我们通过采样的方式构造负样本，50% 来自随机挑选，50% 来自与问题主题词实体相连的其它路径。 

由于 benchmark 数据集 WebQuestion 包含的样本数过少，作者还构造了其他几个数据集： 

Freebase：选取 freebase 中包含出现频率高于 5 次实体的三元组，得到一个知识库子集（含 2.2M 实体和 7K 关系），对于每一个三元组如（subject, type1.type2.predicate, object），我们通过自动化的方式，生成这样的问题答案对： 

Quesiton：“What is the predicate of the type2subject?” Answer：object 

ClueWeb Extractions：由于 Freebase 的三元组都是形式化语言，并不贴近自然语言，我们也用同样的方式将 ClueWeb 上提取出的三元组（subject, “text string”, object）通过少量模板作同样的变换（作者提取了 2M 对三元组）。 

这样我们就在 WebQuestion 数据集的基础上，得到了一个新的扩展数据集，该数据集的例子如下表所示：

可以看出，扩增版的数据集，问题大多数都是自动构造的，缺乏多样性和真实性。怎么办呢？我们希望训练数据中问题的分布式表达尽量贴近它所类似的真实问题的分布式表达。

因此，作者在 WikiAnswers 中抓取了 2.2M 问题（不含答案），通过问题的分类标签，将它们分为了 350k 个类簇（可以理解为每个类簇里的自然语言问题它所表达的意思是一样的）。

如下表所示：

接下来我们就可以进行一个多任务学习（multi-task），让同一个类簇的问题得分较高，即，其训练方式和之前训练答案和问题得分是一样的。

至此，通过以上两种训练，我们的分布式表达就训练完毕了。

4. 论文实验与总结

根据问题首先要确定候选答案，这里作者确定候选答案的方式和信息抽取略有不同。首先在从问题中主题词对应的知识库实体出发，通过 beam search 的方式保存10个和问题最相关的实体关系（通过把实体关系当成答案，用 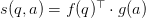 式子的得分作为 beam search 的排序标准）。

接下来选取主题词两跳范围以内的路径，且该路径必须包含这 10 个关系中的关系，将满足条件的路径的终点对应的实体作为候选答案，其中，1 跳路径的权值是 2 跳的 1.5 倍（因为 2 跳包含的元素更多）。 

确定完候选答案后，选取  得分最高的作为最终答案。 

该方法在 WebQuestion 数据集上进行测试，取得了 39.2 的 F1-Score。 

可以看出，相比信息抽取和语义解析的方法，该方法几乎不需要任何手工定义的特征（hand- crafted features），也不需要借助额外的系统（词汇映射表，词性标注，依存树等）。

相对来说，比较简单，也较容易实现，能取得 39.2 的 F1-score 得分（斯坦福 13 年的语义解析方法只有 35.7）也说明了该方法的强大性。通过自动化的方式扩展数据集和多任务训练也部分解决了实验数据不足的缺点。 

然而，向量建模方法，是一种趋于黑盒的方法，缺少了解释性（语义解析可以将问题转化成一种逻辑形式的表达，而信息抽取构造的每一维特征的含义也是离散可见的），更重要的是，它也缺少了我们的先验知识和推理（可以看出其 F1-score 略低于 14 年使用了大量先验知识的信息抽取方法，该方法 F1-score 为 42.0），事实上，这也是现在深度学习一个比较有争议的诟病。 

就这篇论文的向量建模方法来说，也存在一些问题，比如对问题的向量表示采用了类似词袋模型的方法，这样相当于并未考虑问题的语言顺序（比如 “谢霆锋的爸爸是谁？” 谢霆锋是谁的爸爸？ 这两个问题用该方法得到的表达是一样的，然而这两个问题的意思显然是不同的），且训练分布式表达的模型很简单，相当于一个两层的感知机。这些问题，可以通过深度学习来解决。

随着深度学习的加入，KB-QA 进入了一个新的时代。下一期，我们将进入深度学习篇，由于深度学习可以对传统的三种方法都可以进行提升，因此我们打算将深度学习篇拆成 2-3 篇来进行讲解，进一步揭开 KB-QA 的面纱，敬请期待本系列后续文章。

* 本文经授权转载自微信公众号：智言科技AI（zhiyan_AI）

关于PaperWeekly

PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域，欢迎在公众号后台点击「交流群」，小助手将把你带入 PaperWeekly 的交流群里。