DeepMind提出可微分逻辑编程，结合深度学习与符号程序优点

本文经AI新媒体量子位（公众号 ID: QbitAI）授权转载，转载请联系出处。

夏乙 编译自 DeepMind Blog
量子位 出品 | 公众号 QbitAI

神经网络的强大功能有目共睹，但它往往需要大量与目标测试领域数据分布相似的训练数据；而用于符号领域的归纳逻辑编程只需少量数据，却无法对抗噪声，适用领域也很狭窄。

DeepMind在最近发表的一篇论文中，提出了可微分归纳逻辑编程方法∂ILP，既能解决传统归纳逻辑编程擅长的符号类任务，也对噪声数据、训练集中的误差有一定容忍度，还可以通过梯度下降来训练。

怎么样？我们来看看DeepMind在官方博客上对这种方法的解读：

想象一下踢足球的场景，球到了你脚下，你决定把它传给没人盯防的前锋。这个看似简单的行为，需要两种不同的思维。

首先，你认识到自己脚下有一个球，这需要的是直观的感性思维——你没办法简单地描述出你是怎么知道脚下有个球的。

其次，你决定把球传给特定的一个前锋。这个决策需要概念性思维，你的决定依赖于理由——你把球传给这个前锋的原因，是没有人盯防她。

这种区别对我们来说很有意思，因为这两类思维对应着两种不同的机器学习方法：深度学习和符号程序合成（symbolic program synthesis）。

深度学习专注于直观的感性思维，而符号程序合成专注于概念性的、基于规则的思考。这两个系统各有各的优点，深度学习系统能适用于噪声数据，但难以解释，而且需要大量训练数据；符号系统更易于解释，需要的训练数据也更少，但一遇到噪声数据就不行了。

人类认知将这两种截然不同的思维方式无缝结合在了一起，但想要把这种结合复制到一个AI系统里，我们还不太清楚是否可能、如何做到。

我们最近在《JAIR》期刊（Journal of AI Research）上发表的论文表明，系统可以将直观的感性思维和概念性的可解释推理结合起来。我们所描述的∂ILP（可微分归纳逻辑编程，Differentiable Inductive Logic Programming）系统具有下列特性：抗噪声、数据上很经济、能产生可解释的规则。

我们用一个归纳任务来演示∂ILP的工作原理：

已知一对表示数字的图片，系统需要根据左侧图像数字是否小于右侧图像的数字，输出0或1的标签，如下图所示：

解决这个问题涉及两种思维方式。从图像中认出数字，需要直观的感性思维；要整体理解“小于”关系，则需要概念性的思考。

其实，如果给标准的深度学习模型（例如带有MLP的卷积神经网络）提供足够的训练数据，它能学会有效地解决这个问题，训练完成后给它一对从未见过的新图像，它也可以正确分类。

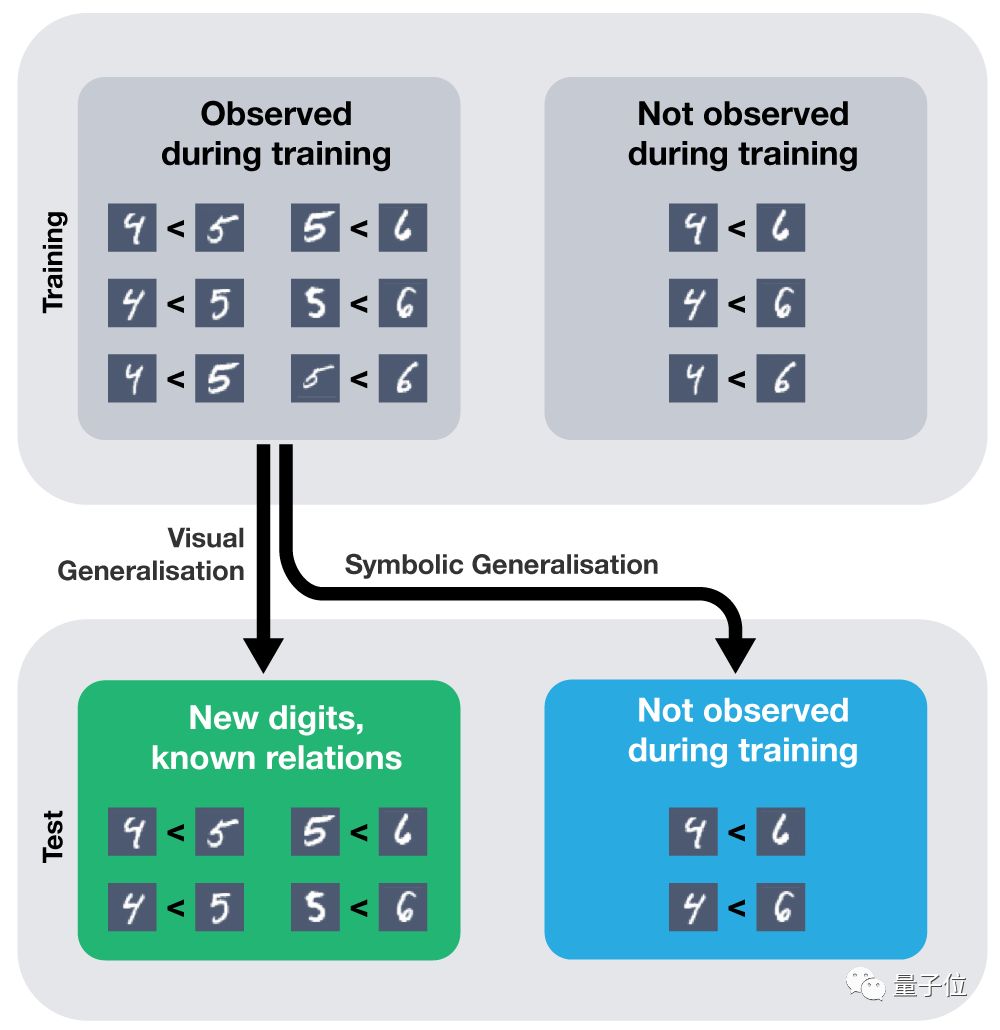
但实际上，只有每对数字你都给它多个样例，它才能正确地泛化。这个模型擅长视觉上的泛化，比如说测试集中的每一对数字它都见过了，要泛化到新的图像，就很容易（见下图绿色方块）。但它不适用于符号的泛化，比如说它就不能泛化到从未见过的数字（见下图蓝色方块）。

马库斯（Gary Marcus）、Joel Grus等研究者最近都撰文指出了这一点。

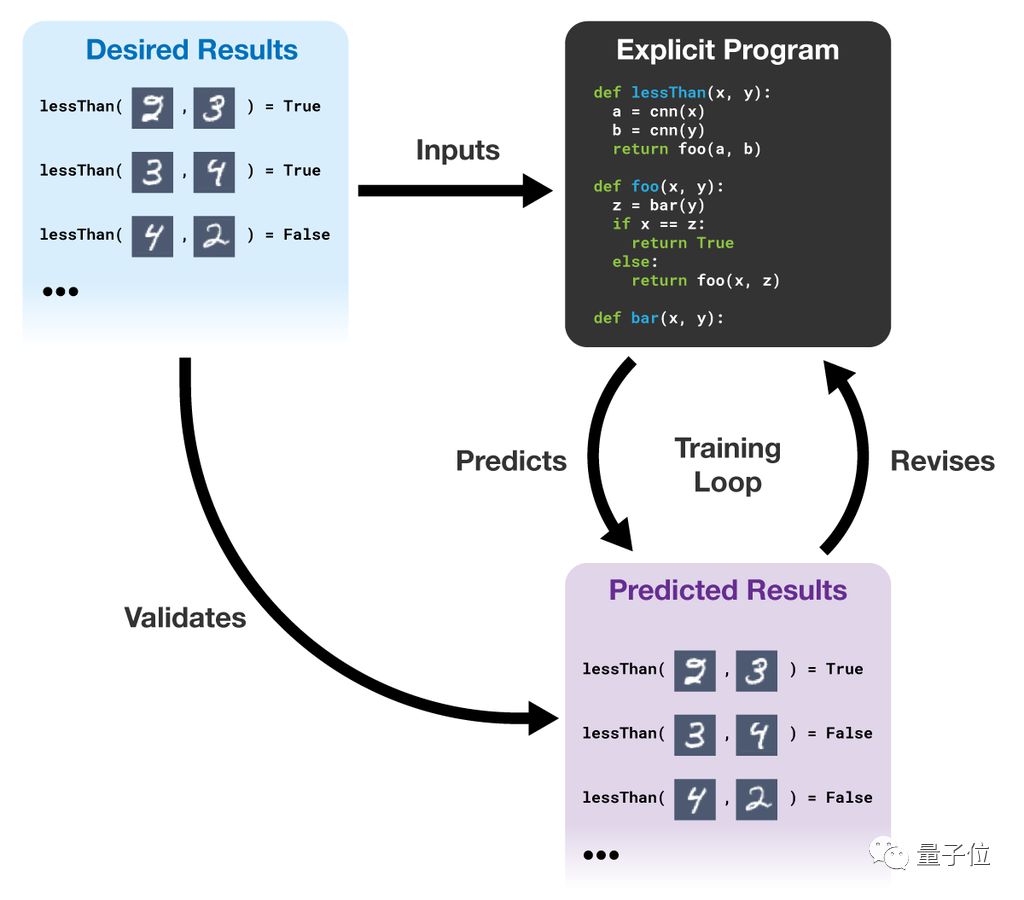
不同于标准的神经网络，∂ILP能够进行符号的泛化；它和标准的符号程序也不一样，可以进行视觉上的泛化。∂ILP从样例中学习可读、可解释、可验证的，明确的程序。已知部分样例（也就是预期的结果，下图中的desired results），∂ILP能生成一个满足需求的程序。它用梯度下降从程序空间中搜索，如果程序的输出与参考数据需要的输出相冲突，系统就会修改程序以更好地匹配数据。

∂ILP的训练过程如下图所示：

∂ILP能进行符号性的泛化，给它足够多x<y、y<z、x<z的样例，它就能考虑到“小于”关系可能具有传递性。一旦它掌握了这条一般规则，就可以将它应用到从未见过的新数字对上去。

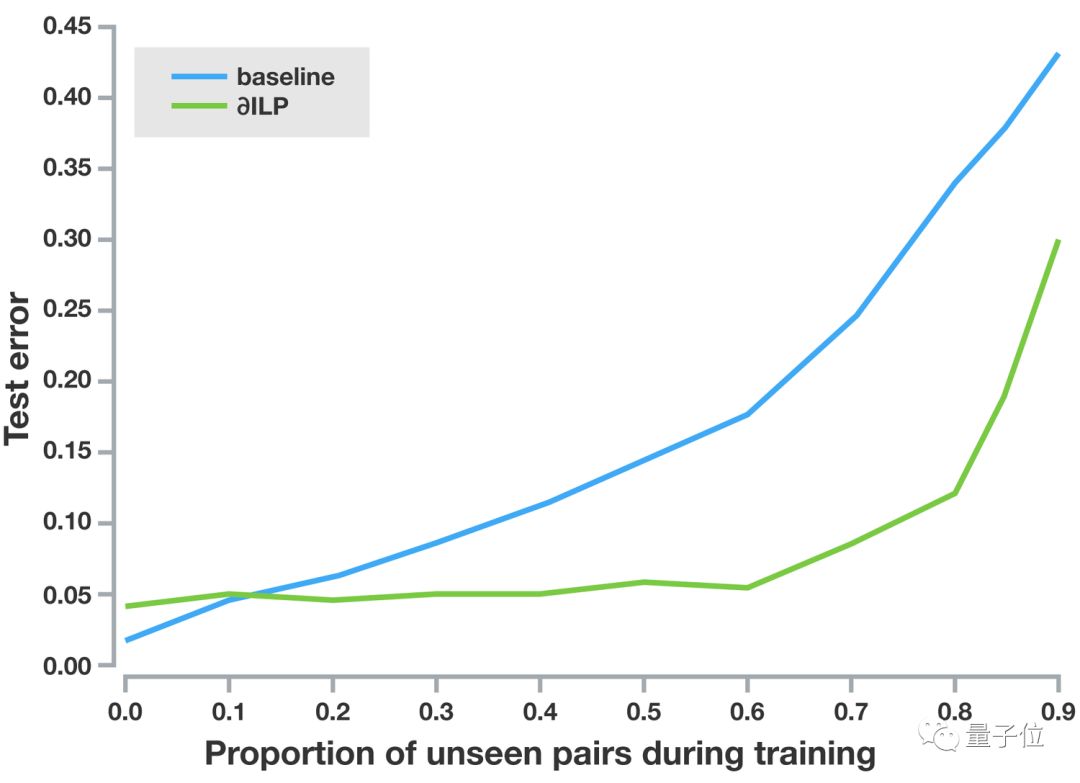
上图总结了我们的“小于”实验：蓝色曲线表示标准的深度神经网络，无法正确泛化到从未见过的数字对，相比之下，在只用40%数字对训练过的情况下，绿色曲线表示的∂ILP依然能保持较低的测试误差。这表明，∂ILP能够进行符号性的泛化。

我们相信，对于深度神经网络中是否能够实现符号泛化这个问题，我们的系统能够在某种程度上给予答案。今后，我们计划将类似∂ILP的系统集成到强化学习智能体以及更大的深度学习模块中，赋予系统推理、反应的能力。

相关论文：

Learning Explanatory Rules from Noisy Data
Richard Evans, Edward Grefenstette
http://www.jair.org/media/5714/live-5714-10391-jair.pdf

原文地址：

https://deepmind.com/blog/learning-explanatory-rules-noisy-data/

— 完 —

量子位 QbitAI · 头条号签约作者

վ'ᴗ' ի 追踪AI技术和产品新动态