基于反向传播NEAT算法的神经网络演化

来源：otoro

编译：weakish

编者按：Google Brain的hardmaru创造了一个demo，使用遗传算法以生成高效而不同寻常的神经网络结构，分类TensorFlow Playground中的数据集。你可以亲自尝试这个demo的效果，地址：http://otoro.net/ml/neat-playground/。

动机

TensorFlow Playground是Google发布的TensorFlow在线Demo。如果你还没有试用过，我建议你去试试看。这个精心设计的在线Demo可以展示基于几个仿制数据集处理一个简单的分类问题的神经网络训练进度。网络的许多方面都可以自定义，例如层数，每层的神经元数和激活函数，初始输入特征等。

我最感兴趣的事情之一是demo用户的反应。人们开始尝试不同的神经网络配置，例如实际需要多少神经网络层来适应某个数据集，或者应该为另一个数据集使用什么样的初始特征。还有哪个激活函数更适合哪个数据集？

在典型的基于神经网络的分类问题中，数据科学家基于人类启发来设计和组合预定义的神经网络，而任务中的机器学习实际上是由网络的权重集合完成的，也就是利用随机梯度下降的一些变体和反向传播算法来计算权重梯度，以使网络在特定的正则化约束下拟合特定的训练数据。TensorFlow Playground刻画了这类任务的本质，但我一直在思考的问题是机器学习是否也可以有效地用于设计针对给定任务的实际神经网络。如果我们能够自动化发现神经网络架构的过程呢？

我决定通过创建这个demo来试验这个想法。我们不会用传统方法组织许多具有统一的激活函数的神经元层，而是尝试彻底放弃层的概念，让每个神经元都可以连接到网络中的任何其他神经元。同时，我们不会坚持使用sigmoid或relu之类的统一的激活函数，而将允许具有多种类型的激活函数（如sigmoid、tanh、relu、 sine、gaussian、abs、square，甚至包括加法门和乘法门）的多种类型的神经元。

我们将使用名为NEAT的遗传算法让我们的神经网络从一个非常简单的初始网络演化成更复杂的神经网络（经过许多代演化）。神经网络的权重将通过反向传播调整。karpathy创造的recurrent.js库很赞，这个库可以用来构建具有任意激活函数的任意神经网络的计算图表示。我实现了NEAT算法来生成recurrent.js可以处理的神经网络表示，NEAT发现的神经网络可以基于recurrent.js进行前向传播，并通过反向传播优化神经网络的权重。

神经演化

大多数学习机器学习的学生都学过，为了训练一个神经网络，应该定义一个目标函数来测量神经网络执行某个任务的表现，并且使用反向传播来求解这个目标函数对应各个权重的导数，接着使用这些梯度来迭代搜寻良好的神经网络权重集合。该框架被称为端到端训练。

虽然反向传播算法对当前的许多应用而言是最有效的方法，但它当然不是唯一的方法。还有其他方法来调整神经网络的权重。举一个极端的例子，一种方法是随机猜测神经网络的权重，直到我们得到可以帮助我们执行某个任务的权重集合。

遗传算法离随机猜测仅有一步之遥。它的工作原理如下：想象一下，如果我们的神经网络有100个随机权重集合，我们评估对应每个权重集合的神经网络，看看它执行一定任务的表现。评估之后，我们只保留最佳的20个权重集合。我们将每组权重转换为一维数组。接着，我们可以从我们保存的20个集合中进行随机选择，取代剩余的80个权重集合，同时应用简单的交配和突变运算来构成新的权重集合：

简单的交配和突变的例子（图片来源：www.abrandao.com）

新的80个权重集合将是前20个权重的突变组合，一旦再次具备了100个权重，我们可以重复进化过程直到我们获得满足需求的权重集合。

这类算法是神经演化的一个例子，该方法用于求解难以定义数学性状良好的目标函数（例如没有明确导数的函数）的神经网络的权重非常好用。我曾使用这种简单的方法来训练神经网络平衡倒立的钟摆，玩软泥排球，并让代理共同学习以躲避障碍。

尽管这种方法易于实现，易于使用，但它并不能很好地伸缩，特别是在网络规模超过一千个连接的情况下。排球代理的大脑只有十几个激活函数。深度Q学习（Deep Q Learning）和策略梯度之类现代方法将允许我们训练用于这些控制任务的（更大的）网络，或基于反向传播处理游戏任务。话是这么说，我敢打赌，我的简单排球代理仍然能打败DQN :-)

过去几年的深度学习研究给了我们许多有用的工具来有效地使用反向传播来完成许多机器学习任务。除了权重正则化之外，我们还有dropout、rmsprop（均方根传播）、批量归一化等方法。因此，我觉得，随着研究人员发现将更多问题纳入端到端框架的方法，未来反向传播仍会是一个训练神经网络的好方法。

除了权重搜索之外，深度学习研究还产生了许多强大的神经网络架构，这些架构是重要的构件。从历史上看，大多数神经网络架构都是由才华横溢的人手工打造的。例如，LSTM门是手工打造的，以避免RNN的梯度衰减问题。创造卷积网络是为了最小化计算机视觉问题所需的连接数量。设计残差网络是为了能够高效地堆叠多层神经网络。通常情况下，在这样的创新架构被发现和被主流学术研究适应之后，其他研究人员事后回顾的时候会意识到实际上这样的发现多么简单，很遗憾他们不能第一个想到这个主意。

我认为神经演化是神经网络架构设计的重要工具。遗传算法不仅仅能够发现神经网络连接的权重，它也可以被扩展，用来发现整个神经网络。我认为使计算机能够自动发现新的神经网络架构是一个非常酷的想法，所以我创建了这个简单的demo来探索这个概念。

演化神经网络拓扑

增强拓扑神经演化（Neuroevolution of Augmenting Topologies，NEAT） 是一种基于遗传算法演化新型神经网络的方法。它是Ken Stanley十多年前发表的，流行于关注演化计算的AI研究人员的非主流小社区。在深度学习占统治地位的主流机器学习研究中，演化计算当然不流行。深度学习的研究人员像是AI社区的流行乐偶像，而非主流研究人员更像是一些没有人听说过的晦涩难懂的车库独立金属乐队。

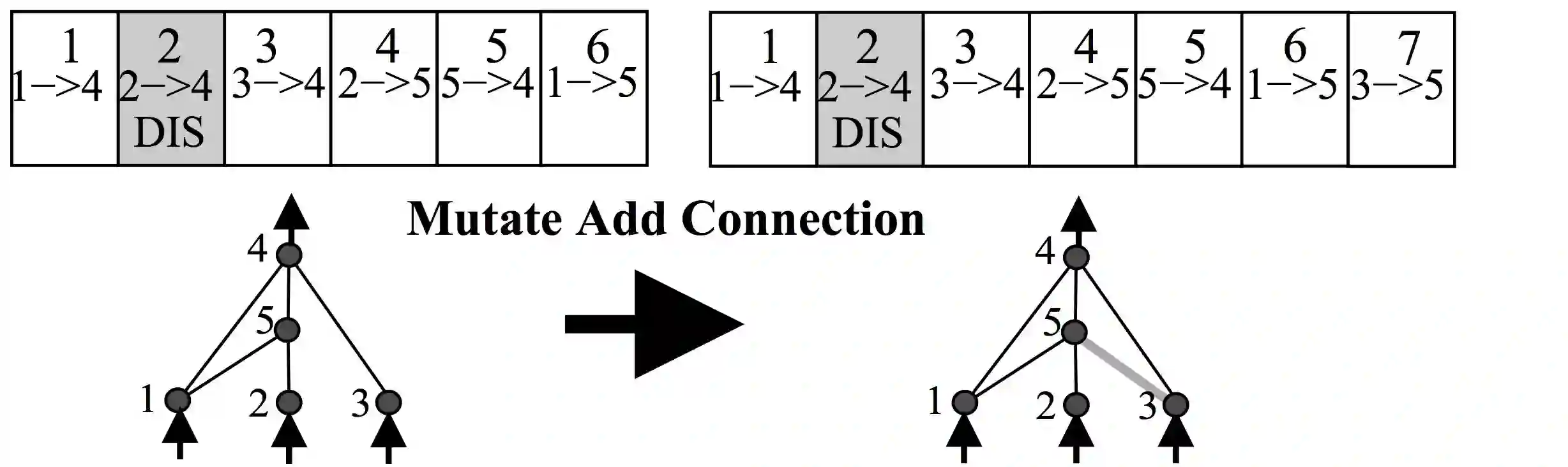
反正NEAT的工作方式是将神经网络表示为连接列表。一开始，网络的初始种群将有一个非常简单的架构，比如每个输入信号和偏置直接连接到输出，中间没有隐藏层。在突变运算中，有一定的概率会创建新的神经元。新的神经元将被放置在现有的连接之间，因此在引入一个新的神经元之后会创建一个新的连接，如下所示：

同时也有一定的概率，在一次突变运算中会创建一个新的连接，如下所示：

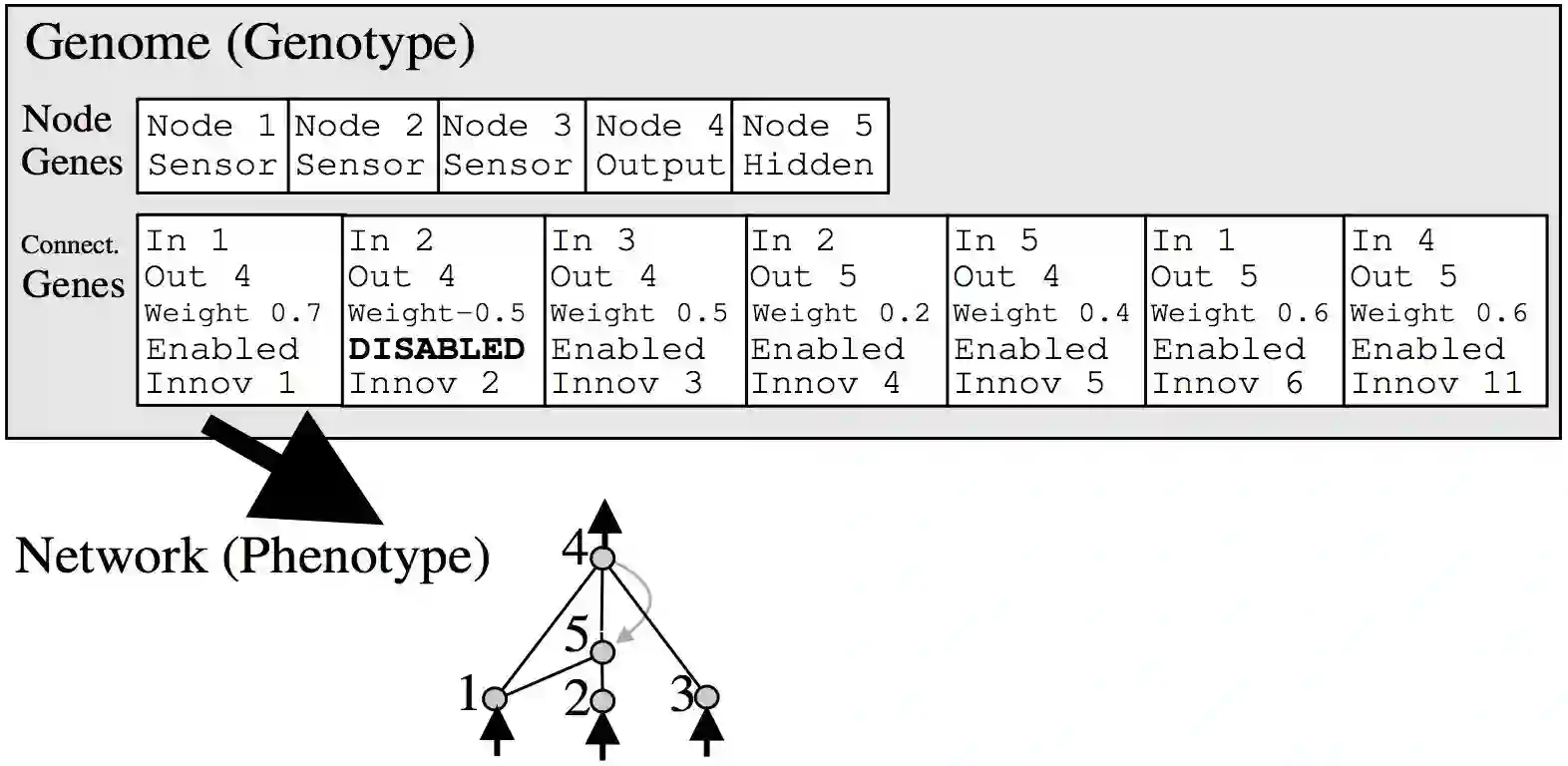
在整个种群中，每个神经元和连接是唯一的，会分配一个唯一的整数标签。所以每个网络只是一个连接的列表，以及这些连接相应的权重。注意，两个不同的网络可以有类似的连接，但每个网络的权重通常不会一样。

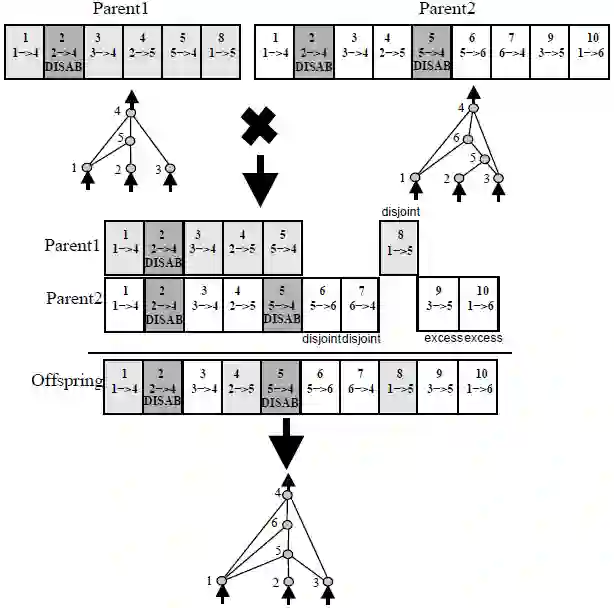
因为每个神经元和每个连接都是全局唯一的，所以有可能合并两个不同的网络，以产生一个新网络。这正是NEAT中的交配运算：

NEAT原论文中所附的示意图，强烈推荐阅读这篇论文

交配运算相当强大。如果我们有一个擅长某个子任务的网络，另一个擅长于某个其他子任务的网络，我们可以培育一个后代网络，这个后代网络可能集上一代网络所长，在执行更大的任务时比上一代网络表现更好。

定义了突变和交配运算之后，我们可以简单地使用前面介绍的遗传算法演化许多代网络，从而发现新的网络。但是，还没到时候，因为NEAT算法不止包括这些遗传运算。

物种形成

在演化计算中，物种形成分组基因群，组与组之间物种不同。有些成员可能不是最擅长执行任务的，但是行为和那些当前表现最好的成员看起来很不一样。物种形成让这些成员有更多的时间充分发展它们的潜力，而不是在每一代杀死这类成员。

想象一个只有狼和企鹅的孤岛。如果我们顺其自然，企鹅在第一代之后将成为死肉，只剩下狼群。但是如果在岛上创建一个安全区（no kill zone），设定狼群进入这个区域后不允许杀死企鹅，那么就会有一定数量的企鹅永远存在，并且有时间演变成飞行企鹅，回归存在大量植被的大陆，而狼群将永远停留在岛上。也有可能，一个有身份认同危机的怪狼和一只企鹅坠入爱河，在这个区域组建一个家庭，说不定最终会产生一群飞行狼企鹅，并逐渐统治大陆。物种形成是人工演化中一个强大的概念。

举一个更具体的例子，考虑前文100个权重集合的例子。想象一下，如果我们修改算法，不是只保留最好的20个集合，并剔除剩余的集合，而是首先根据相似性将100个权重集合分成5组，比方说，根据权重之间的欧几里得距离。现在我们有5个小组，或者说物种，每个小组由20个网络组成。同样，每个小组我们只保留前20％的成员（因此每个物种我们保留4个权重集合），并剔除其余的16个集合。然后我们可以决定通过交配-突变每个物种留下的4个成员，来繁衍剩余的16个成员，或者基于整个种群中所有存活的成员繁衍下一代。这样修改遗传算法以允许物种形成之后，特定类型的基因有时间充分发挥其全部潜力，而且多样性将导向嵌入不同物种的最佳部分的更好的基因。没有物种形成的话，种群容易陷入局部最优。

NEAT论文还定义了物种形成的方法。它定义了一个距离运算符来衡量一个网络和另一个网络的差异度。基本上，它计算两个网络不共享的连接数量，以及共享的连接数量，测量共同连接内部权重的差异，两个网络之间的距离是这些因素的线性组合。一旦我们计算出种群中每个网络之间的距离，NEAT规定了一个公式，这一公式把一定距离内的网络分为一组，以形成一个物种或一个子种群。论文列出了一些关于如何处理不同物种的想法，以及何时进行物种杂交，何时实施物种灭绝的细节。

我个人的看法是，物种形成的概念固然很重要，但如何达成物种形成的具体实现是很灵活的，没有事实上的标准方案。在我实现这个demo的NEAT算法时，我其实忽略了NEAT的物种形成方法，最终使用K-Medoids算法，根据计算出的网络间距，将100个网络的种群分成5个聚类。我们不能使用K均值聚类，因为我们只知道每个网络之间的距离，而不知道每个网络在超维空间中的具体位置。这个方法最后取得了不错的效果，对于本demo中的简单分类任务来说，我觉得这个方法更优雅、更简单。

反向传播NEAT

忘了Torch、Tensorflow和Theano。我决定使用JavaScript实现反向传播NEAT，因为数据科学道场（Data Science Dojo）认为JavaScript是深度学习的最佳语言。

我在之前的Neurogram项目中实现了NEAT的遗传运算部分。这个项目允许用户使用NEAT风格的交配和突变运算交互式地演化一个神经网络种群。生成图片中每个像素的坐标是神经网络的输入，输出则是该像素的颜色。网络越复杂，最终得到的图片就越具体。

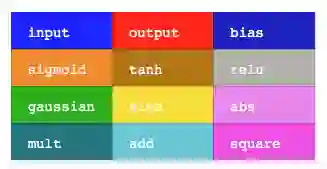
在我们的NEAT实现中，我允许使用许多种类的激活函数，这些激活函数在神经网络中以不同颜色表示：

add运算符对输入没有任何影响（这是输入连接的输出的加权总和），而mult运算符则将所有的加权输入相乘。sine运算符使网络可以在输出时生成重复的纹理。square和abs运算符可用于生成对称性。gaussian运算符可以帮助绘制一次性聚类区域。

从某种意义上讲，TensorFlow Playground中的分类问题可以看成是图像生成问题的一个子集。训练集中的每个数据点对应一个类（零个或一个），每个数据点都有一个(x, y)坐标。如果我们修改艺术生成程序，使其输出一个零到一之间的实数，而不是三个颜色通道，我们可以尝试让艺术生成程序只绘制一个黑白图像，黑白图像中的亮度低于0.5的区域对应于预测为零，高于0.5的区域对应于预测为一。

因此，修改Neurogram的NEAT代码，不生成图像，转而执行分类任务是相当直接的。我们唯一需要做的是实现物种形成部分的算法，使网络演变为适合拟合训练数据的专门网络，而不是生成珍奇艺术的网络。

由于我的NEAT实现通过可由recurrent.js处理的计算图来表示神经网络，因此我们还能够执行反向传播并优化每个单独神经网络架构的权重以最好地拟合训练数据。这样，NEAT严格负责想出新架构，反向传播则可以尝试确定NEAT提供的每个架构的最佳权重集合。在最初的NEAT论文中，NEAT也被用来基于遗传算法计算权重，但我认为这根本不高效，特别是我们知道反向传播是用于得出简单分类问题的权重的更好方法。在我的实现中，在每个网络上执行反向传播时，我还会加入一个针对权重的L2正则化项。以后，我也可能实现其他技术，比如dropout。

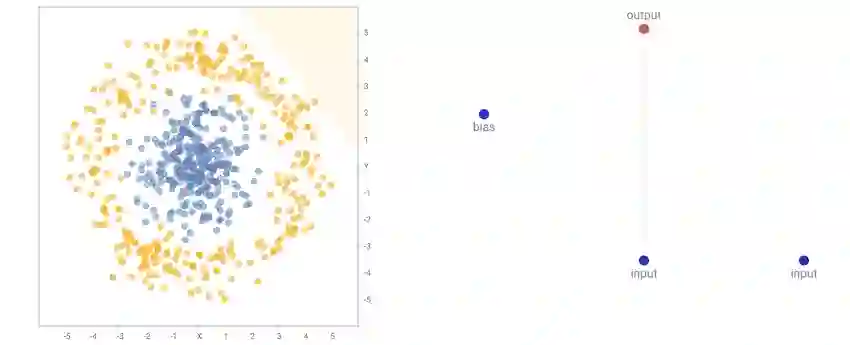
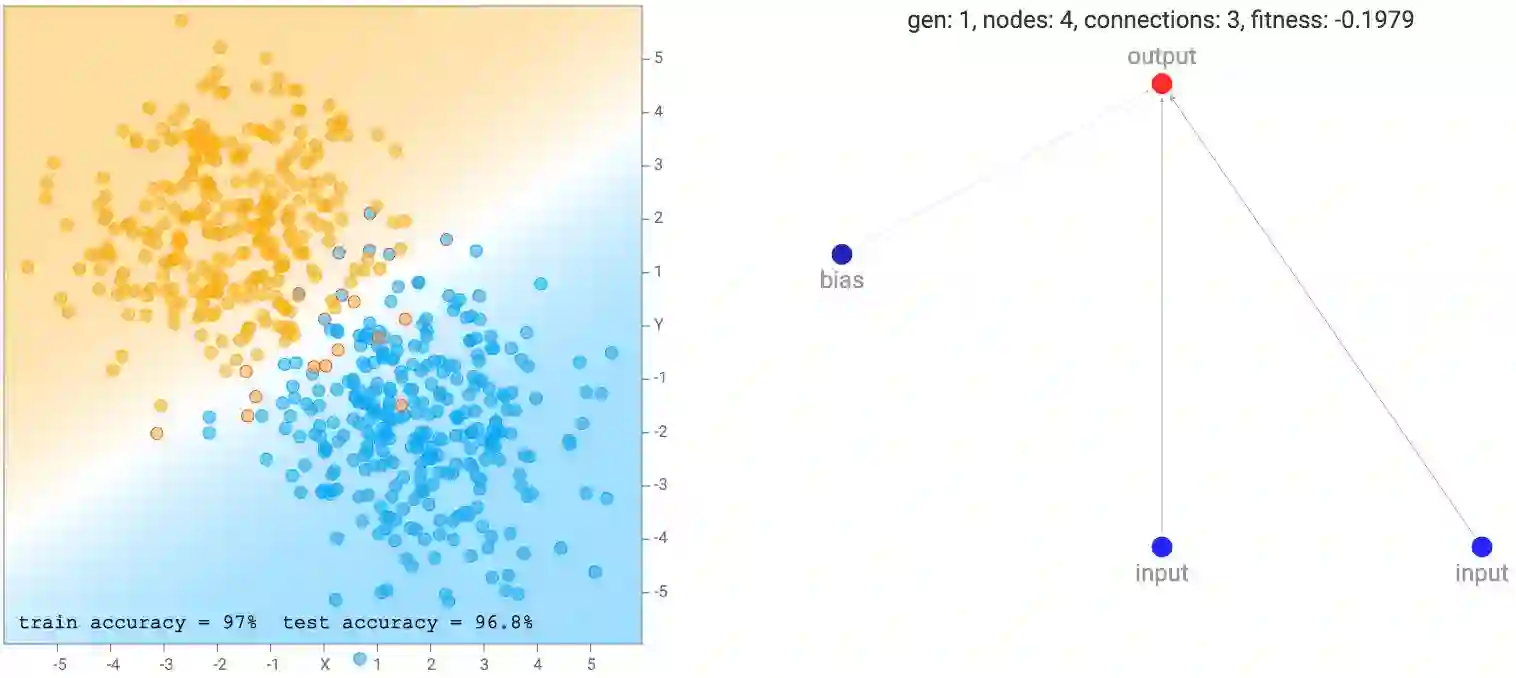
一开始，网络的种群看起来非常简单和最小化，如下所示。请注意，对于这个demo而言，输出神经元也是一个sigmoid算子，因为我们将通过标记为零或一的类进行分类。所以基本上初代网络都是具有不同的随机初始权的逻辑回归网络。

output = σ(w_1 * x + w_2 * y + w_3 * b)

这个简单的网络只是将坐标线性组合成一个sigmoid层，sigmoid层不过是如上图所示，将平面划分成由一条线分开的两部分。输出接近于零的区域将被涂成橙色。接近于一的区域将被涂成蓝色，而零到一之间的区域将是两种颜色的混合，而位于0.5的区域将完全是白色的。我们看到，当数据集是两个高斯聚类时，最简单的默认网络已经表现得相当好了。实际上，刚开始由纯粹的随机权重构成的100个简单网络的初始种群，在应用任何反向传播或遗传算法之前，种群中的最佳网络对于这种类型的数据集而言已经足够好了。

在评估每个网络时，我们需要为每个网络分配一个拟合评分，以便在遗传算法中进行排序。除了基于最大似然衡量每个网络对训练数据的拟合程度，连接的数量也会影响网络的拟合评分。如果有回归精度相同的两个网络，我们会选择较简单的那个网络，而不是较复杂的那个。在某些情况下，我们甚至会选择一个相对而言简单很多的网络，而不是一个非常复杂的网络，即使较简单的网络在拟合训练数据方面表现得不那么精确。为了达到这个目的，我把拟合评分乘以一个与连接数的平方根成比例的因子。

拟合度 = -回归错误 * sqrt(1 + 连接数惩罚 * 连接数)

相比具有更少连接的网络，具有更多连接的网络的拟合评分会是一个更大的负值。我使用了平方根函数，因为我觉得有51个连接的网络应该和有50个连接的网络差不多，而有5个连接的网络和有4个连接的网络大不一样。其他凹型效用函数可能会达到相同的效果。从某种意义上说，就像权重的L2正则化一样，这种惩罚是神经网络结构本身的正则化的一种形式。

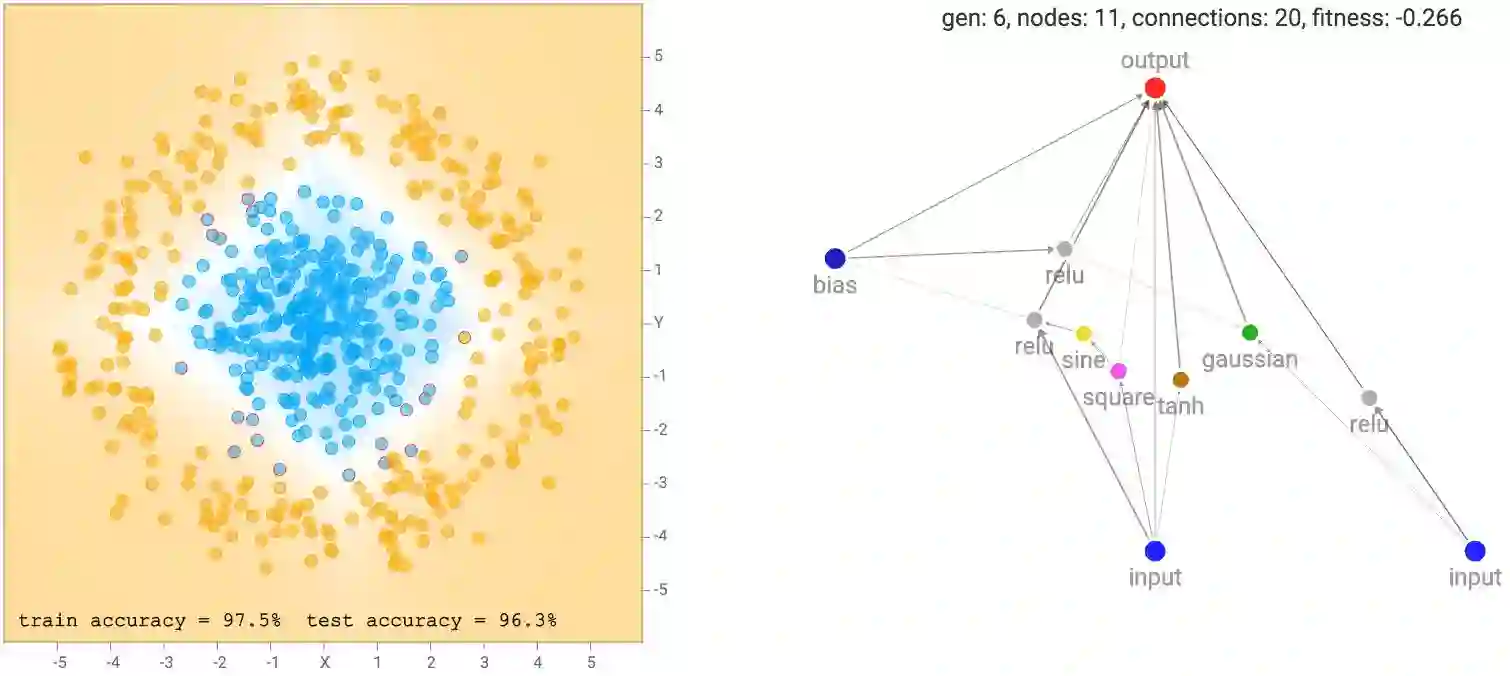
经过几代NEAT进化步骤（在计算拟合评分之前在每个网络上执行了反向传播），我们最终得到一些试图拟合训练数据的网络：

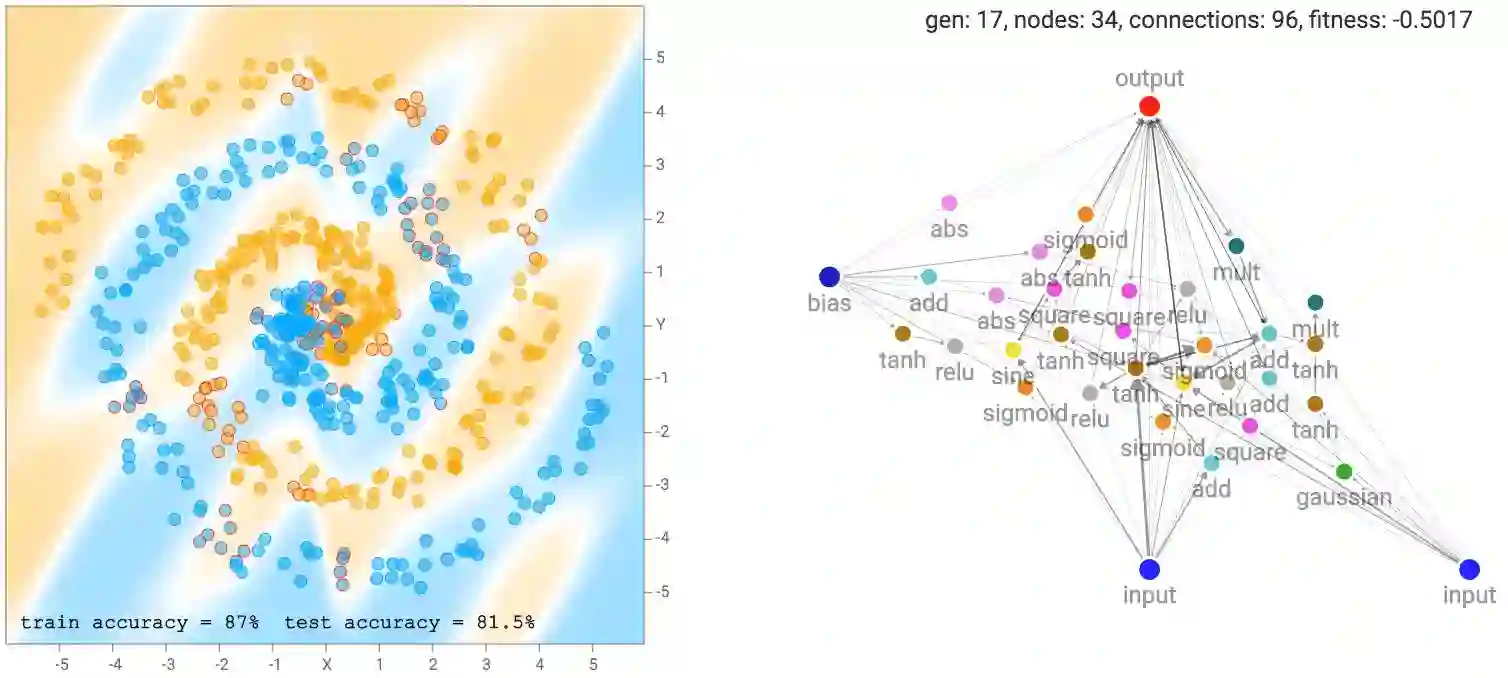
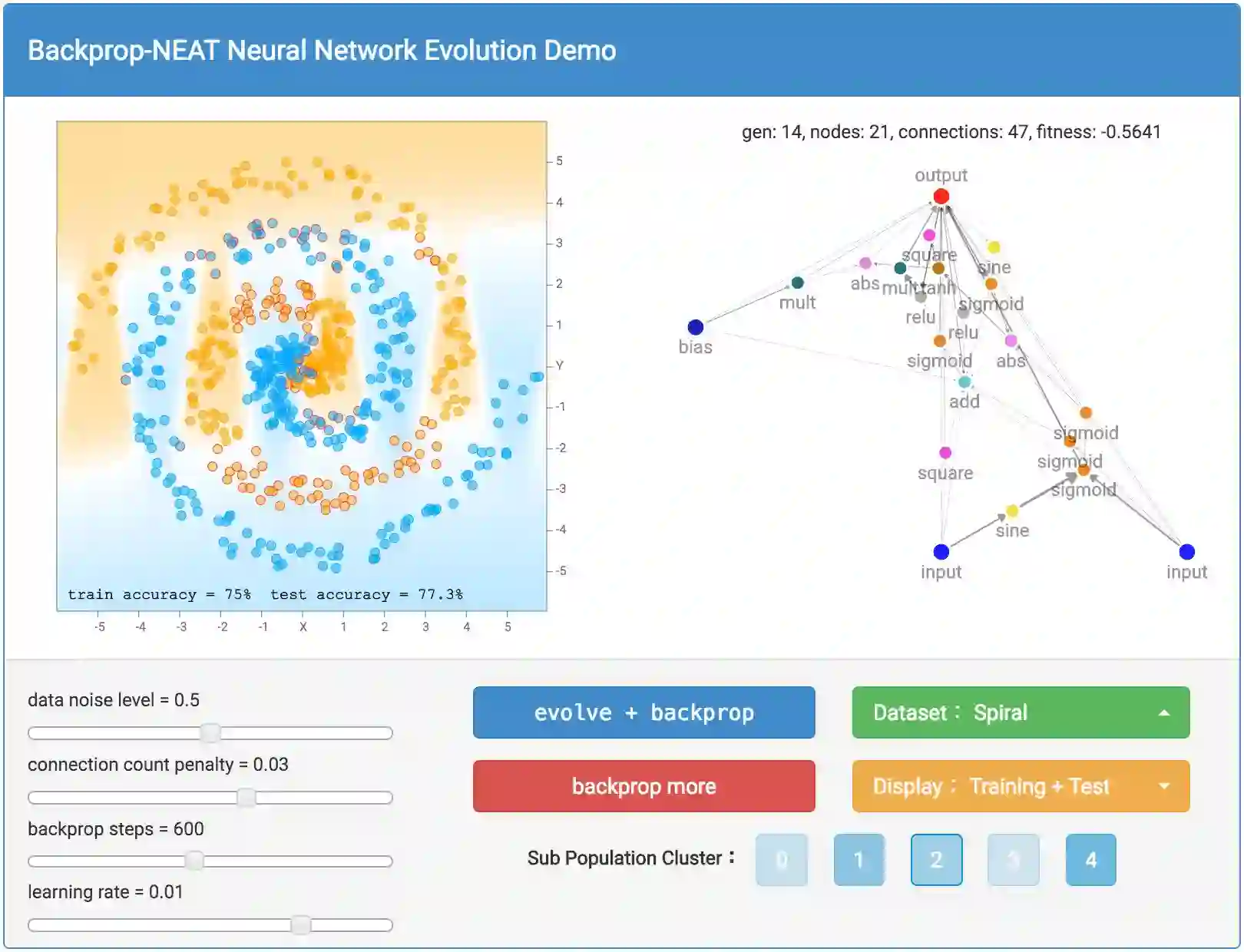
更复杂的数据集，比如螺旋型的数据集需要更复杂的网络以拟合训练数据。

演化过程

在我的实现中，我保持了100个网络的固定种群规模。正如前面所讨论的，我使用K-Medoids算法将子种群数量固定为5，因此整个种群将被聚类为5组，每组由20个类似的网络组成。

在演化步骤中，每个子网络的下一代将通过以下方法创建：随机选择同一子网络的上一代的两个网络（同一个网络可能被选中两次），使用和拟合评分成比例的概率进行加权。所以得分更高的网络将有更大的可能性被选中进行交配并繁衍下一代。NEAT算法的交配+突变遗传算子将在这一步骤中应用，因此，相比于前一代，下一代网络平均而言会具有更多的神经元和连接，来自不同神经元类型的新型激活函数将被实验性地选用于下一代，看看它们是否能改善网络。

但是有时下一代相对于当前一代来说实际上并没有提供任何改进，即使有的话，所有新的神经元和连接对于手头的任务而言也可能都是无用的。为了应对这个问题，我还保留了上一代最优秀的10个网络，并将它们储存在一个特殊的名人堂基因库中，这样每一代的最佳成员都会被克隆出来以备将来使用，以防孩子们都比父母变笨了。迈克尔·乔丹的儿子不太可能在篮球上超过迈克尔·乔丹。在这个世界中，你可能需要与自己正当盛年的父母竞争。

在计算每个网络的拟合评分之前，将对每个网络进行反向传播以优化其权重。默认情况下，每个网络将被反向传播600次。之后，它们的逻辑回归误差将结合一个惩罚连接数量的因子来计算每个网络的拟合得分。拟合评分将在下一个演化过程中再次使用。

在每一代演化之后，我们有50％的概率迫使表现最差的物种灭绝，杀死所有20个成员。为了弥补出现的20个缺口，我们允许上一代表现最好的物种繁衍20个额外的后代。如果企鹅随着时间的过去不学习飞行，我们会让狼进入。这将导致表现最好的物种被分成两个亚种，之后朝不同的方向发展。

使用Demo

好了，讨论了遗传算法，NEAT和反向传播的细节之后，我们终于可以讨论具体如何使用这个demo探索不同的选项。

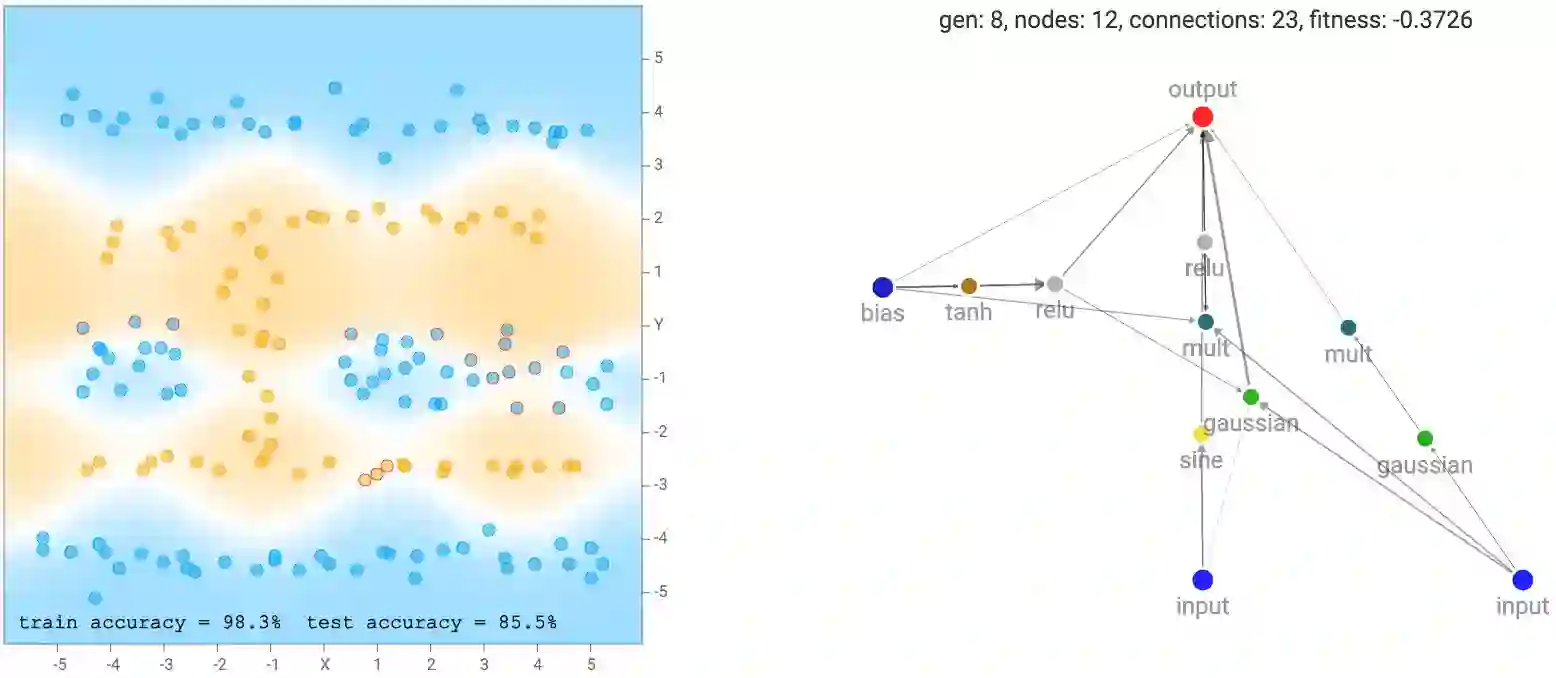
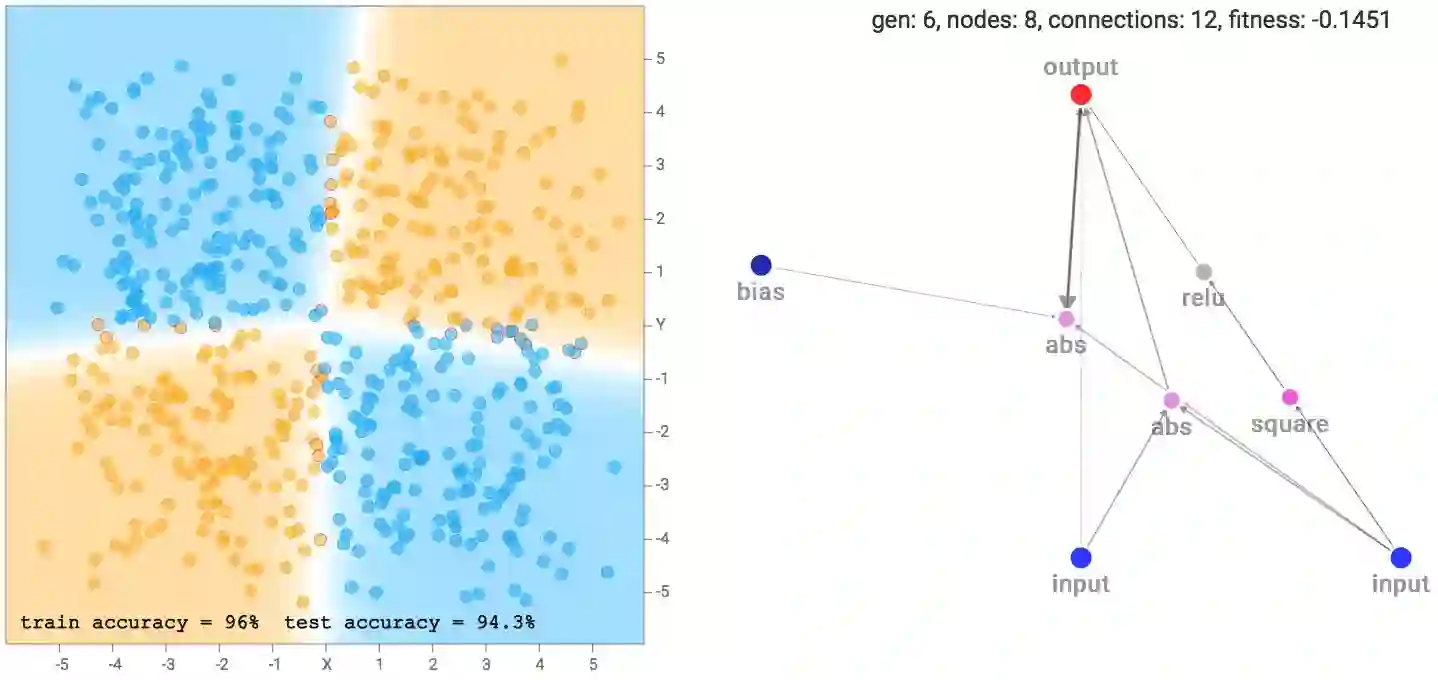
首先，我们使用绿色按钮选择数据集。我镜像了TensorFlow Playground中使用的数据集，所以如果你愿意的话，可以比较下结果。其中包括大圈套小圈的数据集，XOR数据集，由2个高斯聚类组成的数据集，以及一个更具挑战性的螺旋数据集。每个数据集的随机性可以通过左边的data noise level滑杆设置。你也可以随时重置数据集。Demo还包括了定制数据集模式，所以你可以通过鼠标和触摸板创建你自己的数据集。

一半的生成数据将属于训练集，另一半则将属于测试集。通过橙色按钮可以选择显示训练集还是测试集。

定制数据集，数据点越多越好

按下蓝色的evolve + backprop按钮后，魔法生效了。这个按钮将如前一节中描述的那样演化100个网络的一代，然后在新一代的每个网络上执行反向传播。有时候，如果你认为网络还没有达到局部最优，那么你可能需要尝试进一步反向传播，对于规模非常庞大的网络来说，情况很可能会如此。所以Demo包括一个红色的backprop more按钮，以允许纯粹的反向传播，而不进行演化。另外，我们可以通过调整相应的滑杆来控制每次反向传播的步数，以及学习速率。

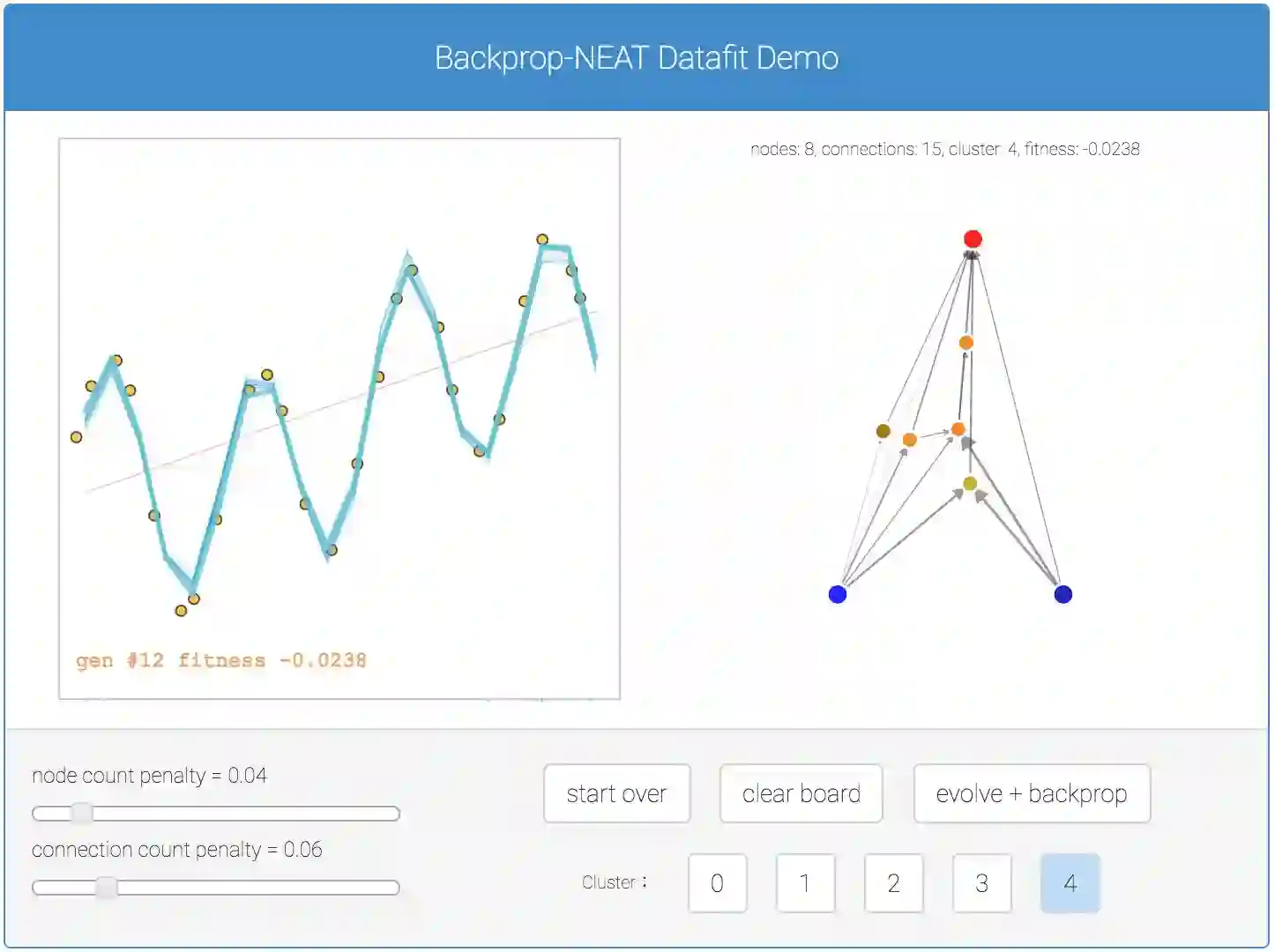
点击evolve + backprop或backprop only按钮之后，屏幕右侧会绘制拟合评分最高的网络，包含所有神经元和连接。较粗的连接线意味着权重的绝对值较大。计算出的分类区域和分类精确性也将显示在屏幕的左侧。除了绘制分类区域之外，错误预测的样本周围会有红色的小圈以指示预测错误。网络上方会显示代数、神经元数、连接数，以及最佳网络的拟合评分。如前所述，拟合评分还取决于连接计数惩罚因子，该因子的大小可以通过左下角的滑杆控制。

你还可以选择查看5个子种群各自的最佳网络。每个子群体都对应一个按钮，点击其一，将显示该子群体的最佳网络，所有相关信息都将基于该网络。这允许你查看不同物种的不同结构，并欣赏种群的（被迫）多样性。默认选中最佳子群体，因此显示的会是最佳网络。子种群按钮颜色的相对明暗表示每个子种群的最佳成员的相对拟合评分，越凝固越强。

结果

TensorFlow Playground中，用户可以作弊，直接将一些预定义的特征应用到输入上，比如，平方、乘法、正弦，然后将输入和所有这些手工的预处理特征传入多层神经网络。这有利于人类直观地识别数据集中的特征，并选择好的特征来计算，以简化神经网络的任务。例如，如果数据集是大圈套小圈，我们知道界限将是半径，甚至半径的平方，所以先对两个输入进行平方运算，那就完成了大部分网络需要做的工作了。

我感兴趣的是遗传算法能否通过演化过程自己发现这些特征，并通过额外的激活函数，将这些特征计算纳入实际的神经网络，而不是依靠人类手工设计。因此，每个NEAT网络的原始输入将只是x和y坐标，偏置为1。任何特征，如平方、相乘、正弦，都必须由算法来发现。

我注意到，大圈套小圈的数据集，最终网络更可能由sine、square、abs激活门组成，因为给定数据集是对称的。而对于XOR数据集，往往趋向于更多的ReLU激活函数，因为数据集需要ReLU函数来生成基本上是直线和尖角的界限。

我注意到的一个更有趣的事情是，相比梯度膨胀的恶劣网络，反向传播良好的网络在演化过程中更容易受到青睐，因为权重值膨胀的网络更可能给出垃圾的分类结果，从而导致很差的拟合评分。将反向传播步数调低，或者调高学习速率，可能导致遗传算法产生不同类型的网络，这些网络在那样的环境中表现会更好。

因此，对一个特定网络而言，即使存在一个能准确拟合训练数据的权重集合，如果反向传播条件不允许该网络学习该权重集合，这个网络最终可能被演化抛弃。这也许可以类比生活中的情况，智商极高的人，如果生活在崇尚单纯的蛮力和弱肉强食的蛮族时代（barbaric era）这样非常恶劣的环境中，可能永远无法发挥其全部潜力。即使在现代，智力高的人如果缺乏人际能力，无法影响社会中的同类，使自己的想法被接受，也可能会失败。

以后的工作

分类问题以外，我之前还创建了一个类似的demo，基于反向传播NEAT处理回归问题。

我感兴趣的另一个任务是基于演化来发现新类型的小型神经网络构件，比如LSTM模块，这些模块通常在更大的深度神经网络或者递归神经网络中重复使用。给定一个深度学习任务和大量的GPU（每隔几个月就会变得更容易负担），或许在未来，基于不断演化的小型神经网络构件，并行训练100个深度网络几十次会是可行的，看看能否在这一过程中发现能够很好地解决特定问题的新类型的小型网络构件。

也许“A”可以演化？（图片来源：colah.github.io）

感谢很多之前帮助我测试这个神经演化网络demo的朋友，以及他们宝贵的改进意见。

GitHub代码仓库：https://github.com/hardmaru/backprop-neat-js

原文地址：http://blog.otoro.net/2016/05/07/backprop-neat/