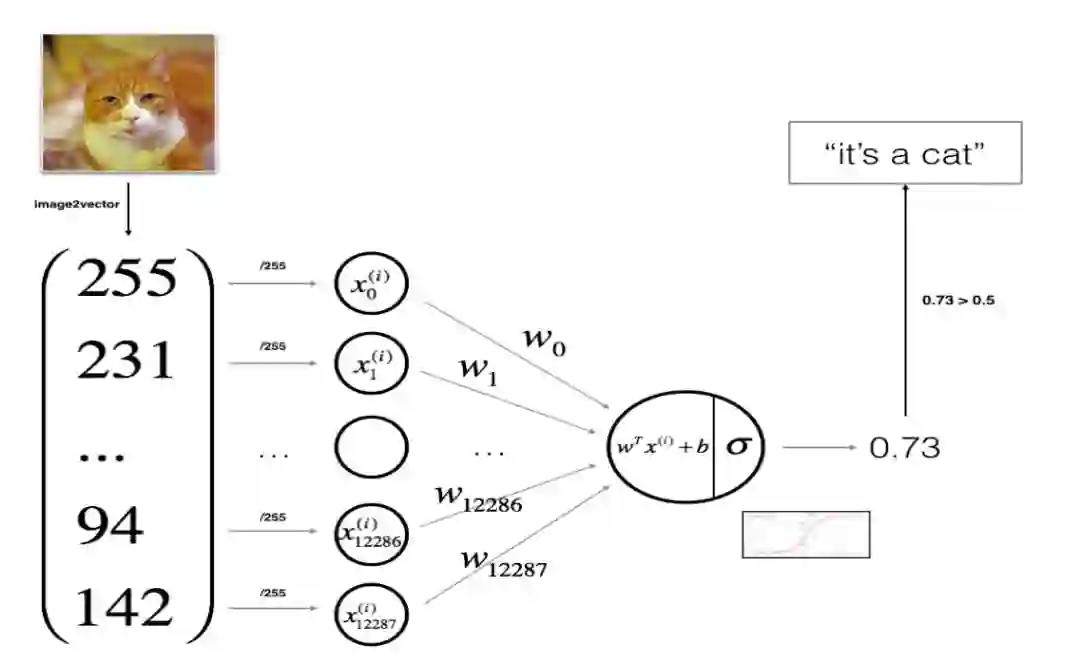
从零开始深度学习：利用numpy手写一个感知机

    很多人说深度学习就是个黑箱子，把图像预处理之后丢进 tensorflow 就能出来预测结果，简单有效又省时省力。但正如我在上一篇推送中所说，如果你已是一名功力纯厚的深度学习工程师，这么做当然没问题。但我想大多数人也和我一样，都是走在学习深度学习的路上，一上来就上框架并没有什么特别不妥之处，但总归是对你理解深度学习的黑箱机制是了无裨益的。所以，我建议在学习深度学习的路上，从最简单的感知机开始写起，一步一步捋清神经网络的结构，以至于激活函数怎么写、采用何种损失函数、前向传播怎么写、后向传播又怎么写，权值如何迭代更新，都需要你自己去实现。若在一开始就直接调用框架，小的 demo 可以跑起来，糊弄一时，看起来就像是鸠摩智在内力未到的情形下强行练习少林寺的 72 绝技，最后走火入魔。

    无论你是在看那本深度学习的花书，还是在学习 Adrew NG 的 deeplearningai，或者是在cs231n 课程，对神经网络的基本理论了如指掌的你一定想亲手用 python 来实现它。笔记1就在不借助任何深度学习框架的基础上，利用 python 的科学计算库 numpy 由最初级的感知机开始，从零搭建一个神经网络模型。

感知机结构

    对于感知机模型、神经网络理论这里就不再叙述，相信志在精通深度学习的你对此一定很熟练了。至于对于神经网络中的输入层、隐藏层、输出层、权重与偏置、激活函数、损失函数、前向传播、反向传播、权值更新、梯度下降、微积分中的链式求导、方向梯度等概念，我也假设你很熟练了。所以，接下来就让我们从零搭建一个最初级的神经网络模型。

    在写代码前，必须先捋一下思路，咱们先要什么，然后再写什么，你心中必须有个数。要从零开始写一个神经网络，通常的方法是：

• 定义网络结构（指定输出层、隐藏层、输出层的大小）

• 初始化模型参数

• 循环操作：执行前向传播/计算损失/执行后向传播/权值更新

    

    有了上面这个思路，我们就可以开始写了。当然了，本节是写一个最简单的感知机模型，所以网络结构就无需特别定义。首先来定义我们的激活函数，激活函数有很多种，这里我们使用大名鼎鼎的 sigmoid 函数：

    直接利用 numpy 进行定义 sigmoid()

import numpy as np
def sigmoid(x):    return 1 / (1 + np.exp(-x))

    在无需定义网络结构的情形下，第二步我们就可以直接对模型参数进行初始化。模型参数主要包括权值 w 和偏置 b ，这也是神经网络学习过程要学的东西。继续利用  numpy  对参数进行初始化：

def initilize_with_zeros(dim):    w = np.zeros((dim, 1))    b = 0.0    #assert(w.shape == (dim, 1))    #assert(isinstance(b, float) or isinstance(b, int))    return w, b

    接下来就要进入模型的主体部分，执行最后一步那个大的循环操作，这个循环中包括前向传播和计算损失、反向传播和权值更新。这也是神经网络训练过程中每一次需要迭代的部分。这里简单说一下，很多初学者容易被这两个概念绕住，前向传播简单而言就是计算预测 y 的过程，而后向传播则是根据预测值和实际值之间的误差不断往回推更新权值和偏置的过程。

前后传播与后向传播

    下面我们来定义一个大的前向传播函数，预测值y为模型从输入到经过激活函数处理后的输出的结果。损失函数我们采用交叉熵损失，利用 numpy 定义如下函数：

def propagate(w, b, X, Y):    m = X.shape[1]    A = sigmoid(np.dot(w.T, X) + b)    cost = -1/m * np.sum(Y*np.log(A) + (1-Y)*np.log(1-A))    dw = np.dot(X, (A-Y).T)/m    db = np.sum(A-Y)/m    
    assert(dw.shape == w.shape)    
    assert(db.dtype == float)    cost = np.squeeze(cost)    
    assert(cost.shape == ())    grads = { 'dw': dw, 
              'db': db    }    
    
    return grads, cost

    在上面的前向传播函数中，我们先是通过激活函数直接表示了感知机输出的预测值，然后通过定义的交叉熵损失函数计算了损失，最后根据损失函数计算了权值 w 和偏置 b的梯度，将参数梯度结果以字典和损失一起作为函数的输出进行返回。这就是前向传播的编写思路。

    接下来循环操作的第二步就是进行反向传播操作，计算每一步的当前损失根据损失对权值进行更新。同样定义一个函数 backward_propagation :

def backward_propagation(w, b, X, Y, num_iterations, learning_rate, print_cost=False):    cost = []    
    for i in range(num_iterations):        grad, cost = propagate(w, b, X, Y)        dw = grad['dw']        db = grad['db']        w = w - learing_rate * dw        b = b - learning_rate * db        
        if i % 100 == 0:            cost.append(cost)        
        if print_cost and i % 100 == 0:            print("cost after iteration %i: %f" %(i, cost))    params = {"dw": w,
              "db": b    }    grads = {"dw": dw,
             "db": db    }    
             
    return params, grads, costs

    在上述函数中，我们先是建立了一个损失列表容器，然后将前一步定义的前向传播函数放进去执行迭代操作，计算每一步的当前损失和梯度，利用梯度下降法对权值进行更新，并用字典封装迭代结束时的参数和梯度进行返回。

    如上所示，一个简单的神经网络模型（感知机）就搭建起来了。通常模型建好之后我们还需要对测试数据进行预测，所以我们也定义一个预测函数 predict，将模型的概率输出转化为0/1值。

def predict(w, b, X):    m = X.shape[1]    Y_prediction = np.zeros((1, m))    w = w.reshape(X.shape[0], 1)    A = sigmoid(np.dot(w.T, X)+b)    
    for i in range(A.shape[1]):        
        if A[:, i] > 0.5:            Y_prediction[:, i] = 1        else:            Y_prediction[:, i] = 0    assert(Y_prediction.shape == (1, m))    
    return Y_prediction

    到这里整个模型算是写完了，但是我们定义了这么多函数，调用起来太麻烦，所以致力于要写出 pythonic的代码的你们肯定想对这些函数进行一下简单的封装：

def model(X_train, Y_train, X_test, Y_test, num_iterations = 2000, learning_rate = 0.5, print_cost = False):    # initialize parameters with zeros     w, b = initialize_with_zeros(X_train.shape[0])        parameters, grads, costs = backward_propagation(w, b, X_train, Y_train, num_iterations, learning_rate, print_cost)      b = parameters["b"]    
    # Predict test/train set examples     Y_prediction_train = predict(w, b, X_train)    Y_prediction_test = predict(w, b, X_test)    
    # Print train/test Errors    print("train accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100))    print("test accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100))    d = {"costs": costs,        
         "Y_prediction_test": Y_prediction_test,         "Y_prediction_train" : Y_prediction_train,         "w" : w,         "b" : b,         
         "learning_rate" : learning_rate,
         "num_iterations": num_iterations}    
    return d

    如此这般一个简易的神经网络就被你用 numpy就写出来了。现在社会浮躁，很多人学习都没有耐心，总是抱着鸠摩智的心态想要一步登天。学习机器学习和深度学习方法很多，但我相信，只有对基本的算法原理每一步都捋清楚，每一步都用最基础的库去实现，你成为一名优秀的机器学习工程师只是时间问题。深度学习第一次推送笔记，加油吧各位！

参考资料：

https://www.coursera.org/learn/machine-learning

https://www.deeplearning.ai/

长按二维码关注“数萃大数据”