1小时赢1000美元的AI赌神是怎样炼成的？幕后团队在线答疑

会员服务 ·

1小时赢1000美元的AI赌神是怎样炼成的？幕后团队在线答疑

2019 年 7 月 20 日 新智元

新智元原创

来源：Reddit

编辑：鹏飞

【新智元导读】德扑被认为是难度远超其他游戏的人工智能挑战项目。然而CMU和Facebook联合打造的AI赌神Pluribus，训练成本150美元、8天训练时间即吊打职业选手，每小时赢1000美元！如此强悍的AI是如何炼成的？要研究其算法该如何入手？有请幕后研究人员为您解答。

人们发现规则明确的游戏，即使像星际这样战局多变的即时战略游戏，人类也无法战胜拥有碾压性算力优势的计算机。于是有人寄希望于带有运气成分、需要大量心里战的德州扑克。

德州扑克（Texas hold'em，有时也简称为Hold'em或Holdem），简称德扑，是世界上最流行的公牌扑克衍生游戏，也是国际扑克比赛的正式竞赛项目之一。德州扑克是位置顺序影响最大的扑克衍生游戏之一，因为所有轮数的下注次序维持不变。它也是美国多数赌场内最受欢迎的扑克牌类游戏，在美国以外的地区也十分流行，理论上一桌同时最多可容纳22位（若不销牌则为23位）牌手，但一般是二至十人一桌。

https://zh.wikipedia.org/wiki/%E5%BE%B7%E5%B7%9E%E6%92%B2%E5%85%8B

赌神下凡：1小时赢7000块，一周炼成百万富翁

扑克是典型的不完美信息博弈游戏。德州扑克中，玩家无法获知已发生事件的全部信息，一对一无限注中包含10^160个决策点（decision points）。

每个点需要根据出牌方的理解，产生不同的路径。这种不完整信息的特质，使得德州扑克成为难度远超其他游戏的人工智能挑战项目。

然而，其实结局早就在暗中被注定了。40年来，科学家就一直没有停止过对德州的研究。

10年前，计算机第一次在有限制的德州扑克游戏中，战胜了人类顶级选手；4年前，来自加拿大阿尔伯塔大学的研究团队开发出Cepheus(仙王座)，一个号称人类无法战胜的扑克机器人；2年前，也就是2017年，加拿大和捷克的科学家在arXiv上发表论文，提出名为DeepStack的算法，称可以让人工智能在比赛中拥有“直觉”。

而前两天，在CMU科学家的努力下，人工智能已经在六人无限注德扑比赛上击败所有人类顶尖玩家。只存在于电影电视剧中的赌神，现在真实的存在于现实世界了！

https://www.nature.com/articles/d41586-019-02156-9

https://science.sciencemag.org/content/early/2019/07/10/science.aay2400

https://www.techmeme.com/

而这个赌神Pluribus的“炼成”却很像一个寒门子弟黑马突袭的故事：用来训练Pluribus的电脑1000块人民币不到，在2块CPU上实施运行。

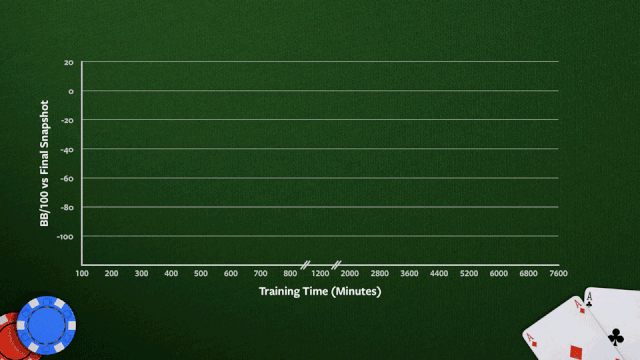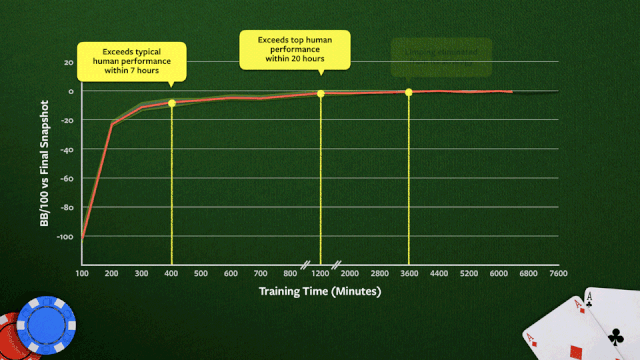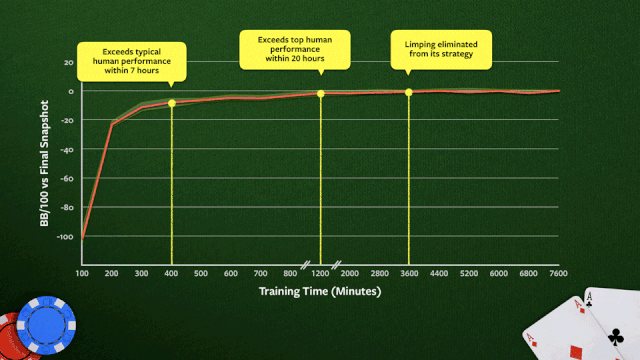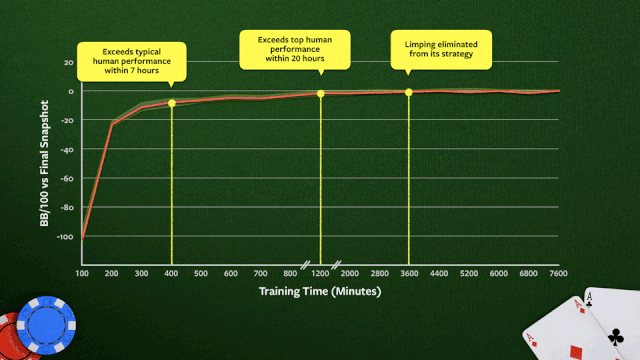
上图显示了在64核CPU训练期间，Pluribus的蓝图策略的改进过程。绩效是根据训练的最终快照来衡量的。

正是凭着这么简陋的装备，Pluribus一小时赢了人类将近7000人民币。按照这样的速度，AI通过德州成为百万富翁，只需要不到一周的时间。

上面的视频中展示了Pluribus 在对阵几位职业玩家时采用的牌局策略。(牌面已公开展示)

赌神是怎么炼成的？幕后科学家在线答疑

显然，赌神AI引爆了大众情绪。技术人员最关心的，除了它能赢钱外，恐怕就是它背后的运作机制了。

近日，这位“AI赌神” Pluribus的幕后推手，Facebook AI Research研究科学家、CMU计算机科学博士在读Noam Brown，以及CMU教授Tuomas Sandholm，共同在reddit发声，揭秘赌神AI幕后花絮，并回答网友提问。大伙儿热情高涨，贡献了超过130个回帖。

会对扑克网站造成影响吗？

最为全世界最受欢迎的扑克游戏之一，德州扑克在美国及世界范围内拥有大量的玩家。大家非常关心AI赌神以后，会不会在短时间内对线上德州扑克产生影响（言外之意：是否会有老千用人工智能冒充真人用户）？此外，Reddit用户DlC3R还问了另一个大家很关心的问题：算法之间的博弈何时开始？

Noam认为，现在主流扑克网站上，都有在用先进的机器人检测技术，并且已经非常成熟，用机器人出老千的风险太大，一点都不值当。但肯定会对职业扑克（例如选手、行业、俱乐部等）产生影响，起码俱乐部可以使用人工智能来训练职业扑克选手。

不过Noam还补充了一句：我们只关注人工智能而非扑克（言外之意，我们只是痴迷与技术钻研的人，其它的，也着实没有时间和精力去顾及许多啦！）

解释一下如何使用AIVAT来减少方差因子

Noam称他们估计机器人的胜率为5bb/100，也就是说，在50美元/100美元的盲注和10000美元的筹码下，如果每个筹码等值1美元，Pluribus平均每手赢得5美元的奖金，这样的话每小时可以赚到1000美元（约等于7000人民币）。

德州扑克盈利计算单位是“每百局赢利大盲注，BB/100（p值为0.021）”。优秀的职业选手能达到3-7BB/100手，显然AI的这个胜率已经非常高了！

如果没有方差减少，那么专业人士可能需要在连续4个月内，每周5天、每天8小时打牌，才能获得有价值的样本量。

感谢阿尔伯塔大学和布拉格查尔斯大学的研究人员开发了名为AIVAT的扑克方差减少算法，最终减少了约12.5倍的手数。

AIVAT可以有效的减少运气的成分，例如，如果机器人有一手牌非常强，AIVAT就会从奖金里减去一个基线值来抵消运气成分。

上面的视频中显示了蒙特卡罗CFR算法通过评估实际和假设行动值，来更新遍历者策略的过程。在Pluribus中，出于优化目的，这种遍历实际上是以深度优先的方式完成的。

研究Pluribus算法应该从何处入手？

一位名为smoke_carrot的人显然是个比较好学的人。他想要认真研究Pluribus背后的算法，但发现Pluribus所使用的方法跟他平时接触的不一样，希望研究人员能给一些指导建议，例如该从哪儿入手？该看哪方面的书籍？

Tuomas教授肯定了这位smoke_carrot的论断，确实Pluribus的算法跟强化学习、MCTS完全不同。而且，目前在解决不完美信息游戏这方面，没有很好的教材。加之这个领域发展过于迅速，以至于2010年到2015年的论文都过时了。

他建议有兴趣想进行深入研究的同学，应该去阅读本次研究的相关论文。目前最新发布的论文还是可以免费获取，这个是需要认真研读的！

随后Tuomas教授精心挑选了一些相关论文以及报告，方便大家进行学习研究：

Keynote “New Results for Solving Imperfect-Information Games” at the Association for the Advancement of Artificial Intelligence Annual Conference (AAAI), 2019, available on Vimeo. (https://vimeo.com/313942390)
Keynote “Super-Human AI for Strategic Reasoning: Beating Top Pros in Heads-Up No-Limit Texas Hold’em” at the International Joint Conference on Artificial Intelligence (IJCAI), available on YouTube. (https://www.youtube.com/watch?v=xrWulRY_t1o)
Solving Imperfect-Information Games. (http://www.cs.cmu.edu/~sandholm/Solving%20games.Science-2015.pdf) Science 347(6218), 122-123, 2015.
Abstraction for Solving Large Incomplete-Information Games. (http://www.cs.cmu.edu/~sandholm/game%20abstraction.aaai15SMT.pdf) In AAAI, Senior Member Track, 2015.
The State of Solving Large Incomplete-Information Games, and Application to Poker. (http://www.cs.cmu.edu/~sandholm/solving%20games.aimag11.pdf) AI Magazine, special issue on Algorithmic Game Theory, Winter, 13-32, 2010.
Brown, N. and Sandholm, T. 2019. Superhuman AI for multiplayer poker. (https://science.sciencemag.org/content/early/2019/07/10/science.aay2400) Science, July 11th.
Farina, G., Kroer, C., and Sandholm, T. 2019. Regret Circuits: Composability of Regret Minimizers. In Proceedings of the International Conference on Machine Learning (ICML), 2019. arXiv version. (https://arxiv.org/abs/1811.02540)
Farina, G., Kroer, C., Brown, N., and Sandholm, T. 2019. Stable-Predictive Optimistic Counterfactual Regret Minimization. In ICML. arXiv version. (https://arxiv.org/pdf/1902.04982.pdf)
Brown, N, Lerer, A., Gross, S., and Sandholm, T. 2019. Deep Counterfactual Regret Minimization In ICML. Early version (https://arxiv.org/pdf/1811.00164.pdf) in NeurIPS-18 Deep RL Workshop, 2018.
Brown, N. and Sandholm, T. 2019. Solving Imperfect-Information Games via Discounted Regret Minimization (https://arxiv.org/pdf/1809.04040.pdf). In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI). Outstanding Paper Honorable Mention, one of four papers receiving special recognition out of 1,150 accepted papers and 7,095 submissions.
Farina, G., Kroer, C., and Sandholm, T. 2019. Online Convex Optimization for Sequential Decision Processes and Extensive-Form Games (http://www.cs.cmu.edu/~gfarina/2018/laminar-regret-aaai19/). In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI).
Marchesi, A., Farina, G., Kroer, C., Gatti, N., and Sandholm, T. 2019. Quasi-Perfect Stackelberg Equilibrium (http://www.cs.cmu.edu/~gfarina/2018/qp-stackelberg-aaai19/). In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI).
Farina, G., Kroer, C., Brown, N., and Sandholm, T. 2019. Stable-Predictive Optimistic Counterfactual Regret Minimization (https://arxiv.org/pdf/1902.04982.pdf). arXiv.
Brown, N. and Sandholm, T. 2018. Superhuman AI for heads-up no-limit poker: Libratus beats top professionals. (http://science.sciencemag.org/content/early/2017/12/15/science.aao1733) Science, full Research Article.
Brown, N., Lerer, A., Gross, S., and Sandholm, T. 2018. Deep Counterfactual Regret Minimization (https://arxiv.org/pdf/1811.00164.pdf). NeurIPS Deep Reinforcement Learning Workshop. *Oral Presentation*.
Kroer, C., Waugh, K., Kilinc-Karzan, F., and Sandholm, T. 2018. Faster algorithms for extensive-form game solving via improved smoothing functions. (https://rdcu.be/8EyP) Mathematical Programming, Series A. Abstract published in EC-17.
Brown, N., Sandholm, T., and Amos, B. 2018. Depth-Limited Solving for Imperfect-Information Games. (https://arxiv.org/pdf/1805.08195.pdf) In Proc. Neural Information Processing Systems (NeurIPS).
Kroer, C. and Sandholm, T. 2018. A Unified Framework for Extensive-Form Game Abstraction with Bounds. In NIPS. Early version (http://www.cs.cmu.edu/~ckroer/papers/unified_abstraction_framework_ai_cubed.pdf) in IJCAI-18 AI^3 workshop.
Farina, G., Gatti, N., and Sandholm, T. 2018. Practical Exact Algorithm for Trembling-Hand Equilibrium Refinements in Games. (http://www.cs.cmu.edu/~gfarina/2017/trembling-lp-refinements-nips18/) In NeurIPS.
Kroer, C., Farina, G., and Sandholm, T. 2018. Solving Large Sequential Games with the Excessive Gap Technique. (https://arxiv.org/abs/1810.03063) In NeurIPS. Also Spotlight presentation.
Farina, G., Celli, A., Gatti, N., and Sandholm, T. 2018. Ex Ante Coordination and Collusion in Zero-Sum Multi-Player Extensive-Form Games. (http://www.cs.cmu.edu/~gfarina/2018/collusion-3players-nips18/) In NeurIPS.
Farina, G., Marchesi, A., Kroer, C., Gatti, N., and Sandholm, T. 2018. Trembling-Hand Perfection in Extensive-Form Games with Commitment. (http://www.cs.cmu.edu/~ckroer/papers/stackelberg_perfection_ijcai18.pdf) In IJCAI.
Kroer, C., Farina, G., and Sandholm, T*. 2018. *Robust Stackelberg Equilibria in Extensive-Form Games and Extension to Limited Lookahead. (http://www.cs.cmu.edu/~ckroer/papers/robust.aaai18.pdf) In Proc. AAAI Conference on AI (AAAI).
Brown, N., and Sandholm, T. 2017. Safe and Nested Subgame Solving for Imperfect-Information Games. (https://www.cs.cmu.edu/~noamb/papers/17-NIPS-Safe.pdf) In NIPS. *Best Paper Award, out of 3,240 submissions.
Farina, G., Kroer, C., Sandholm, T. 2017. Regret Minimization in Behaviorally-Constrained Zero-Sum Games. (http://www.cs.cmu.edu/~sandholm/behavioral.icml17.pdf) In Proc. International Conference on Machine Learning (ICML).
Brown, N. and Sandholm, T. 2017. Reduced Space and Faster Convergence in Imperfect-Information Games via Pruning. (http://www.cs.cmu.edu/~sandholm/reducedSpace.icml17.pdf) In ICML.
Kroer, C., Farina, G., Sandholm, T. 2017. Smoothing Method for Approximate Extensive-Form Perfect Equilibrium. (http://www.cs.cmu.edu/~sandholm/smoothingEFPE.ijcai17.pdf) In IJCAI. ArXiv version. (http://arxiv.org/abs/1705.09326)
Brown, N., Kroer, C., and Sandholm, T. 2017. Dynamic Thresholding and Pruning for Regret Minimization. (http://www.cs.cmu.edu/~sandholm/dynamicThresholding.aaai17.pdf) In AAAI.
Kroer, C. and Sandholm, T. 2016. Imperfect-Recall Abstractions with Bounds in Games. (http://www.cs.cmu.edu/~sandholm/imperfect-recall-abstraction-with-bounds.ec16.pdf) In Proc. ACM Conference on Economics and Computation (EC).
Noam Brown and Tuomas Sandholm. 2016. Strategy-Based Warm Starting for Regret Minimization in Games. In AAAI. Extended version with appendix. (http://www.cs.cmu.edu/~sandholm/warmStart.aaai16.withAppendixAndTypoFix.pdf)
Noam Brown and Tuomas Sandholm. 2015. Regret-Based Pruning in Extensive-Form Games. (http://www.cs.cmu.edu/~sandholm/cs15-892F15) In NIPS. Extended version. (http://www.cs.cmu.edu/~sandholm/regret-basedPruning.nips15.withAppendix.pdf)
Brown, N. and Sandholm, T. 2015. Simultaneous Abstraction and Equilibrium Finding in Games. (http://www.cs.cmu.edu/~sandholm/simultaneous.ijcai15.pdf) In IJCAI.
Kroer, C. & Sandholm, T. 2015. Limited Lookahead in Imperfect-Information Games. (http://www.cs.cmu.edu/~sandholm/limited-look-ahead.ijcai15.pdf) IJCAI.
Kroer, C., Waugh, K., Kilinc-Karzan, F., and Sandholm, T. 2015. Faster First-Order Methods for Extensive-Form Game Solving. (http://www.cs.cmu.edu/~sandholm/faster.ec15.pdf) In EC.
Brown, N., Ganzfried, S., and Sandholm, T. 2015. Hierarchical Abstraction, Distributed Equilibrium Computation, and Post-Processing, with Application to a Champion No-Limit Texas Hold’em Agent. (http://www.cs.cmu.edu/~sandholm/hierarchical.aamas15.pdf) In Proc. Internat. Conference on Autonomous Agents and Multiagent Systems (AAMAS).
Kroer, C. and Sandholm, T. 2015. Discretization of Continuous Action Spaces in Extensive-Form Games. (http://www.cs.cmu.edu/~sandholm/discretization.aamas15.fromACM.pdf) In AAMAS.
Ganzfried, S. and Sandholm, T. 2015. Endgame Solving in Large Imperfect-Information Games. (http://www.cs.cmu.edu/~sandholm/endgame.aamas15.fromACM.pdf) In AAMAS.
Kroer, C. and Sandholm, T. 2014. Extensive-Form Game Abstraction With Bounds. (http://www.cs.cmu.edu/~sandholm/extensiveGameAbstraction.ec14.pdf) In EC.
Brown, N. and Sandholm, T. 2014. Regret Transfer and Parameter Optimization. (http://www.cs.cmu.edu/~sandholm/regret_transfer.aaai14.pdf) In AAAI.
Ganzfried, S. and Sandholm, T. 2014. Potential-Aware Imperfect-Recall Abstraction with Earth Mover’s Distance in Imperfect-Information Games. (http://www.cs.cmu.edu/~sandholm/potential-aware_imperfect-recall.aaai14.pdf) In AAAI.
Ganzfried, S. and Sandholm, T. 2013. Action Translation in Extensive-Form Games with Large Action Spaces: Axioms, Paradoxes, and the Pseudo-Harmonic Mapping. (http://www.cs.cmu.edu/~sandholm/reverse%20mapping.ijcai13.pdf) In IJCAI.
Sandholm, T. and Singh, S. 2012. Lossy Stochastic Game Abstraction with Bounds. (http://www.cs.cmu.edu/~sandholm/lossyStochasticGameAbstractionWBounds.ec12.pdf) In EC.
Gilpin, A., Peña, J., and Sandholm, T. 2012. First-Order Algorithm with O(ln(1/epsilon)) Convergence for epsilon-Equilibrium in Two-Person Zero-Sum Games. (http://www.cs.cmu.edu/~sandholm/restart.MathProg12.pdf) Mathematical Programming 133(1-2), 279-298. Subsumes our AAAI-08 paper.
Ganzfried, S., Sandholm, T., and Waugh, K. 2012. Strategy Purification and Thresholding: Effective Non-Equilibrium Approaches for Playing Large Games. (http://www.cs.cmu.edu/~sandholm/StrategyPurification_AAMAS2012_camera_ready_2.pdf) In AAMAS.
Ganzfried, S. and Sandholm, T. 2012. Tartanian5: A Heads-Up No-Limit Texas Hold'em Poker-Playing Program. (http://www.cs.cmu.edu/~sandholm/Tartanian_ACPC12_CR.pdf) Computer Poker Symposium at AAAI.
Hoda, S., Gilpin, A., Peña, J., and Sandholm, T. 2010. Smoothing techniques for computing Nash equilibria of sequential games. (http://www.cs.cmu.edu/~sandholm/proxtreeplex.MathOfOR.pdf) Mathematics of Operations Research 35(2), 494-512.
Ganzfried, S. and Sandholm, T. 2010 Computing Equilibria by Incorporating Qualitative Models (http://www.cs.cmu.edu/~sandholm/qualitative.aamas10.pdf). In AAMAS. Extended version (http://www.cs.cmu.edu/~sandholm/qualitative.TR10.pdf): CMU technical report CMU-CS-10-105.
Gilpin, A. and Sandholm, T. 2010. Speeding Up Gradient-Based Algorithms for Sequential Games (Extended Abstract) (http://www.cs.cmu.edu/~sandholm/speedup.aamas10.pdf). In AAMAS.
Ganzfried, S. and Sandholm, T. 2009. Computing Equilibria in Multiplayer Stochastic Games of Imperfect Information (http://www.cs.cmu.edu/~sandholm/stochgames.ijcai09.pdf). In IJCAI.

他还补充了2008年以及之前关于不完全信息游戏的计算解决的精选论文：

Gilpin, A. and Sandholm, T. 2008. Expectation-Based Versus Potential-Aware Automated Abstraction in Imperfect Information Games: An Experimental Comparison Using Poker. (http://www.cs.cmu.edu/~sandholm/expectation-basedVsPotential-Aware.AAAI08.pdf) In AAAI.
Ganzfried, S. and Sandholm, T. 2008. Computing an Approximate Jam/Fold Equilibrium for 3-Agent No-Limit Texas Hold'em Tournaments. (http://www.cs.cmu.edu/~sandholm/3-player%20jam-fold.AAMAS08.pdf) In AAMAS.
Gilpin, A., Sandholm, T., and Sørensen, T. 2008. A heads-up no-limit Texas Hold'em poker player: Discretized betting models and automatically generated equilibrium-finding programs. (http://www.cs.cmu.edu/~sandholm/tartanian.AAMAS08.pdf) In AAMAS.
Gilpin, A. and Sandholm, T. 2007. Lossless abstraction of imperfect information games (http://www.cs.cmu.edu/~sandholm/extensive.jacm07.pdf). Journal of the ACM, 54 (5). Early versions in EC-06.
Gilpin, A., Sandholm, T., and Sørensen, T. 2007. Potential-Aware Automated Abstraction of Sequential Games, and Holistic Equilibrium Analysis of Texas Hold'em Poker. (http://www.cs.cmu.edu/~sandholm/gs3.aaai07.pdf) In AAAI.
Gilpin, A. and Sandholm, T. 2007. Better automated abstraction techniques for imperfect information games, with application to Texas Hold'em poker. (http://www.cs.cmu.edu/~sandholm/gs2.aamas07.pdf) In AAMAS.
Gilpin, A. and Sandholm, T. 2006. A competitive Texas Hold'em Poker player via automated abstraction and real-time equilibrium computation. (http://www.cs.cmu.edu/~sandholm/texas.aaai06.pdf) In AAAI.