每周一起读 #02 | ICML 2019:基于粒子的变分推断加速方法
”每周一起读“是由 PaperWeekly 发起的论文共读活动,我们结合自然语言处理、计算机视觉和机器学习等领域的顶会论文和前沿成果来指定每期论文,并且邀请论文作者来到现场,和大家展开更有价值的延伸讨论。
我们希望能为 PaperWeekly 的各位读者带来一种全新的论文阅读体验、一个认识同好、找到组织的契机、一次与国际顶会论文作者当面交流的机会。
6 月 5 日(周三)晚 7 点半,“每周一起读”将邀请清华大学计算机系博士生刘畅,和大家分享他发表于机器学习国际会议 ICML 2019 的两篇最新文章。
刘畅
清华大学计算机系博士生
刘畅,清华大学计算机系博士生,从事统计机器学习方向研究,导师为朱军教授。他于 2014 年在清华大学物理系取得理学学士学位,博士期间曾在杜克大学访学一年。他的研究兴趣主要在贝叶斯推理方法以及利用几何结构的机器学习方法。他在机器学习国际会议 ICML, NeurlPS, AAAI 等上发表了数篇论文。
ICML 2019
Abstract: Particle-based variational inference methods (ParVIs) have gained attention in the Bayesian inference literature, for their capacity to yield flexible and accurate approximations. We explore ParVIs from the perspective of Wasserstein gradient flows, and make both theoretical and practical contributions. We unify various finite-particle approximations that existing ParVIs use, and recognize that the approximation is essentially a compulsory smoothing treatment, in either of two equivalent forms. This novel understanding reveals the assumptions and relations of existing ParVIs, and also inspires new ParVIs. We propose an acceleration framework and a principled bandwidth-selection method for general ParVIs; these are based on the developed theory and leverage the geometry of the Wasserstein space. Experimental results show the improved convergence by the acceleration framework and enhanced sample accuracy by the bandwidth-selection method.
Abstract: It is known that the Langevin dynamics used in MCMC is the gradient flow of the KL divergence on the Wasserstein space, which helps convergence analysis and inspires recent particle-based variational inference methods (ParVIs). But no more MCMC dynamics is understood in this way. In this work, by developing novel concepts, we propose a theoretical framework that recognizes a general MCMC dynamics as the fiber-gradient Hamiltonian flow on the Wasserstein space of a fiber-Riemannian Poisson manifold. The “conservation + convergence” structure of the flow gives a clear picture on the behavior of general MCMC dynamics. The framework also enables ParVI simulation of MCMC dynamics, which enriches the ParVI family with more efficient dynamics, and also adapts ParVI advantages to MCMCs. We develop two ParVI methods for a particular MCMC dynamics and demonstrate the benefits in experiments.
时间:6 月 5 日(周三) 19:30–21:00
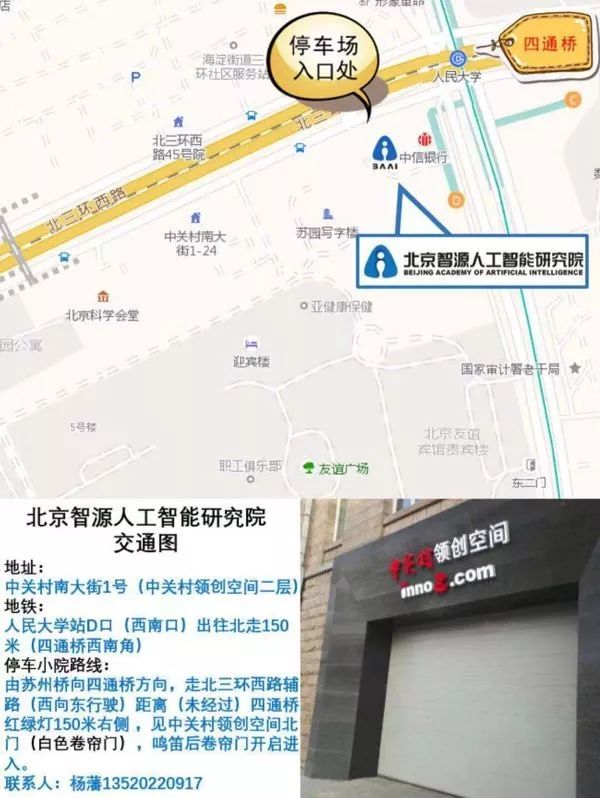
地点:北京智源人工智能研究院6号会议室
北京市海淀区中关村南大街1-1号
中关村领创空间(信息谷)
长按识别二维码,即刻报名👇
报名截止日期:6 月 5 日(周三)12:00
* 场地人数有限,报名成功的读者将收到包含电子门票二维码的短信通知,请留意查收。
注意事项:
* 如您无法按时到场参与活动,请于活动开始前 24 小时在 PaperWeekly 微信公众号后台留言告知,留言格式为放弃报名 + 报名电话;无故缺席者,将不再享有后续活动的报名资格。
1 / 扫码关注
扫码关注 PaperWeekly👇
PaperWeekly
清华大学计算机科学与技术系
北京智源人工智能研究院
🔍
现在,在「知乎」也能找到我们了
进入知乎首页搜索「PaperWeekly」
点击「关注」订阅我们的专栏吧
关于PaperWeekly
PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域,欢迎在公众号后台点击「交流群」,小助手将把你带入 PaperWeekly 的交流群里。
▽ 点击 | 阅读原文 | 立刻报名