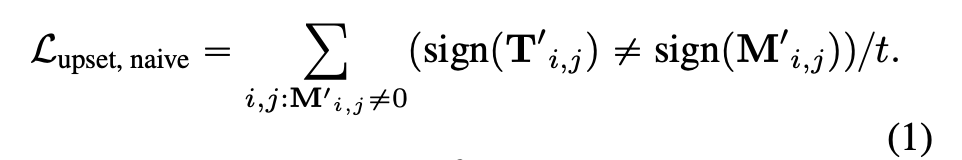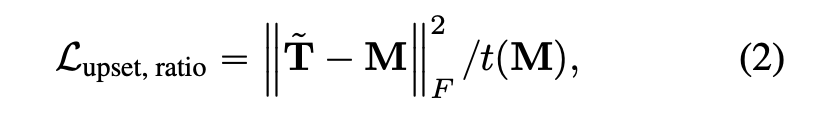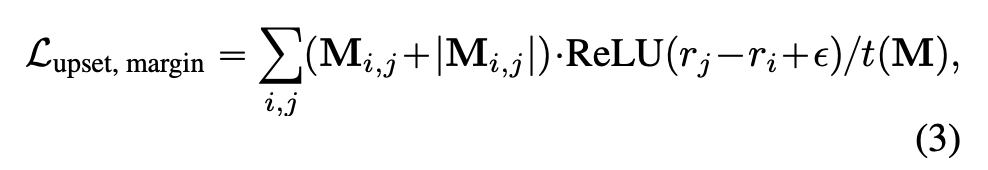ICML2022 | GNNRank: 基于有向图神经网络从两两比较中学习全局排序

会员服务 ·

ICML2022 | GNNRank: 基于有向图神经网络从两两比较中学习全局排序

2022 年 10 月 11 日 PaperWeekly

©作者 | 庄双双

来源 | MIND Laboratory

论文标题：

GNNRank: Learning Global Rankings from Pairwise Comparisons via Directed Graph Neural Networks

论文链接：

https://arxiv.org/pdf/2202.00211.pdf

代码链接：

https://github.com/SherylHYX/GNNRank

从反映相对潜在优势或分数的成对比较中恢复全球排名是信息检索及以后的一个基本问题。在分析大规模数据时，通常会寻求各种形式的数据排名（即排序），来达到识别最重要的条目、有效计算搜索和排序操作或提取主要特征。

在过去的成对比较排名的方法中，主要是基于利用直接从数据构建的适当定义的矩阵算子的特征向量的频谱方法。其中，SerialRank 通过从所谓的序列化问题中引入特定的归纳偏差，显示了对一组没有关系的全序项目进行排序的良好能力：在无噪声设置中，给定足够的成对比较，某个相似性矩阵的 Fiedler 向量可以恢复真实的排序。对称非负矩阵（或图）的 Fiedler 值定义为矩阵的组合拉普拉斯算子的第二小特征值，其对应的特征向量称为 Fiedler 向量，Fiedler 向量能够对图的有用信息进行编码。

目前 GNN 在任务排名中的能力还不够完善。少数现有作品限于特定设置，例如 top-n 个性化推荐和近似中心性度量。另一个技术差距是无法通过直接优化排名目标来学习模型，于是文中提出了 GNNRank 框架，这是一种与现有 GNN 模型兼容的端到端的排名框架，能够学习有向图的节点嵌入。

论文方法

基于有向图神经网络的 GNNRank 框架：

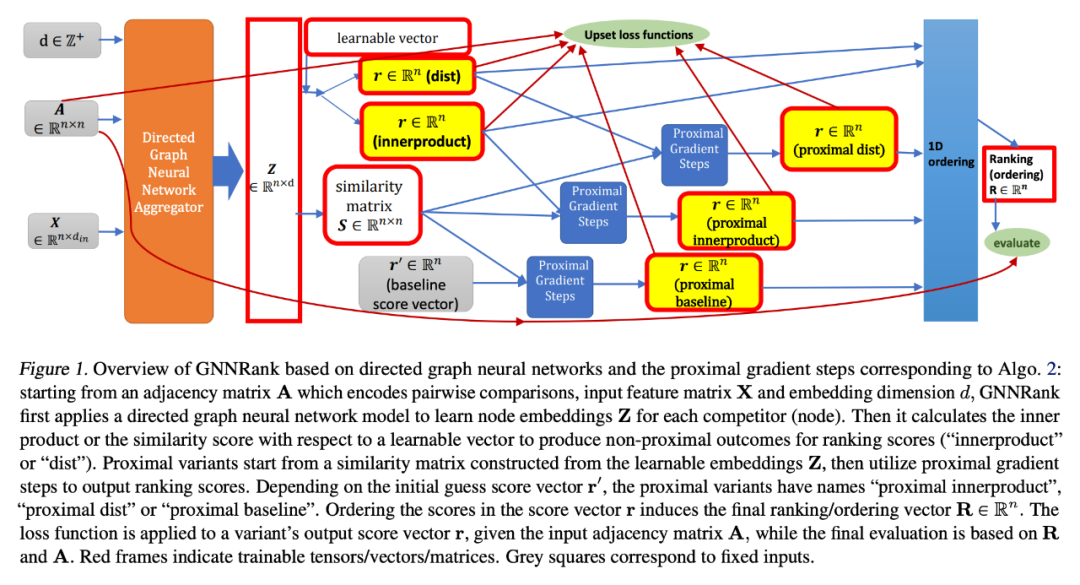
从编码成对比较、输入特征矩阵 X 和嵌入维数 d 的邻接矩阵 A 出发，GNNRank 首先应用有向图神经网络模型来学习每个竞争者 (节点) 的节点嵌入 Z。然后，它计算内积或关于可学习向量的相似性分数，以产生非近端结果的排名分数 (“innerproduct” 或 “dist”)。

近端变体从可学习的嵌入 Z 构建的相似性矩阵开始，然后利用近端梯度步骤输出排名得分。根据初始猜测评分向量 r'，近端变体具有名称 “近端内积” 、“近端 dist” 或 “近端基线”。对分数向量 r 中的分数排序诱导最终排名/排序向量 R。在给定输入邻接矩阵 a 的情况下，将损失函数应用于变量的输出分数向量 r，而最终评估基于 R 和 A。

1.1 Problem Definition

不失一般性，从考虑比赛中的成对比较，这些比较可以在有向图（有向图）𝐺=（𝑉，𝐸）中进行编码。

节点集𝑉： 竞争对手
边集𝐸： 成对比较
邻接矩阵： 匹配的结果

从成对比较中恢复全局排名相当于为每个节点分配一个整数，表示其在竞争者中的位置，其中排名越低，节点越强。我们的办法是，首先尝试为所有节点学习技能级别向量，其中较高的技能值对应于较低的等级排序。

1.2 Motivation and Connection to SerialRank

1. 首先计算某个相似度矩阵图片的拉普拉斯算子。

2. 在全局符号协调之后，对应的 Fiedler 向量用作最终排名估计。

3. 虽然在实践中通常有效，但 SerialRank 的表现重度取决于底层相似度矩阵的质量。

为了解决这个问题，我们引入了一个参数化的 GNN 模型，它允许我们计算可训练的相似性度量，这对后续排名很有用。然而，出于训练目的，当然需要通过计算 Fiedler 向量以某种方式反向传播梯度以更新 GNN 参数。因为通常很难通过特征向量计算直接传递梯度，所以我们将 Fiedler 向量表示为约束优化问题的解。然后，我们使用近端梯度步骤来近似解决这个问题，每个梯度步骤本身都可以根据底层优化变量进行微分，最终通过链式法则，即 GNN 参数。

在文中提出的框架内，过程允许将基于 Fiedler-vector 的排名的归纳偏差与 GNN 的灵活性相结合，以建模实体之间的关系。SerialRank 可以被视为 GNNRank 的特例了；图片计算击败和的竞争对手的数量，加上被和击败的竞争对手的数量，减去击败和之一但被另一个击败的竞争对手的数量，加上节点数量的一半。来自公共邻居的信息可以通过有向 GNN 聚合，并且诸如应用于有向图嵌入的高斯 RBF 内核之类的内核可以近似。

1.3 Loss Functions and Objectives

形式上，设 1 是一个全一列向量，并定义矩阵。然后有

，为了不惩罚初始成对排序不可用的条目，仅在 M1 具有非零条目的位置比较 T1 与 M1。naive upset 损失被定义为：

可微分的翻转损耗则定义为：

另一种选择是边际损失：

使用的训练损失是 Lupset、ratio、Lupset、margin 或它们的总和，其中选择设置为超参数。

1.4 Initialization and Pretraining Considerations

Real-World Data

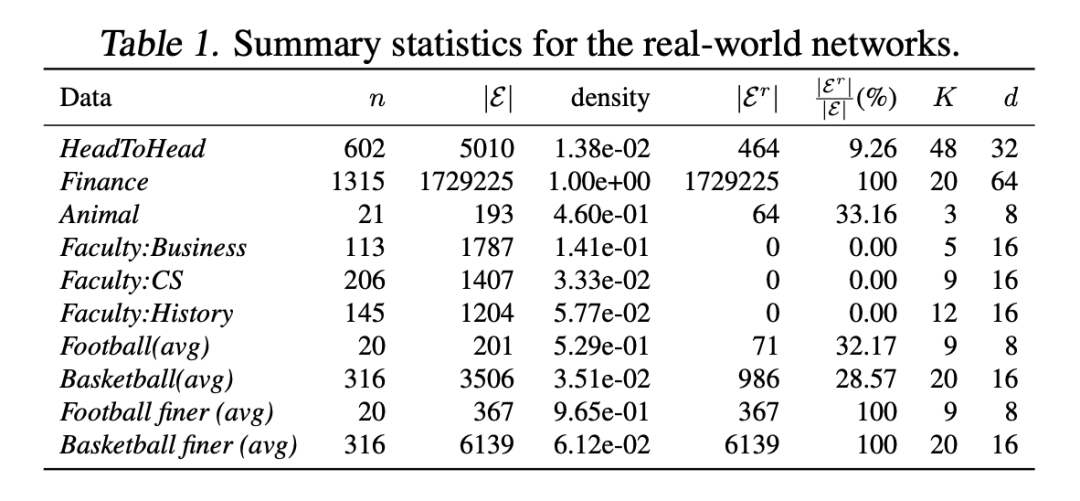
作者考虑了 10 个真实世界的数据集（总共构建了 78 个有向图）。基于成对比较的有向图在大多数情况下构造如下：对于每场比赛，如果比赛结果不是平局，则添加一条边，边权重为得分之间的差异（绝对获胜，即得分），并且平局被视为这对球员之间没有比赛。

表 1 给出了节点数 (n)、有向边数 ( )、双向边数 ( )（自循环的边计算一次，而对于两个不同的节点之间的一条边，双向边计算两次）及其在所有边中的百分比，对于现实世界的网络，说明了网络大小和密度的可变性（定义为）。当输入特征没有被提供时，我们按照 [2] 中的办法生成特征，堆叠的最大 K 个特征向量的实部和虚部用于 GNN 的输入特征。此外我们报告通过有向图 GNN 生成的节点嵌入的维度 d。

Main Experimental Results

模型是根据最低选择的，在没有标签监督的情况下简单获得，其中非近端结果（对于“dist”和“innerproduct”变体）列在“GNNRank-N”列中，近端方法（对于“proximal dist” ，“近端内积”和“近端基线”变体）在所有表中与“GNNRank-P”一起列出。

表 2 作者将两组方法与 10 个真实世界数据集的基线进行了比较，其中篮球数据集是 30 个赛季的平均值，而足球数据集是 6 个赛季的平均值。通过包括更多可训练的参数，本文的近端方法的最佳执行变体在所有真实世界数据集上也优于其 SerialRank。

表 3 显示了对于某些密集的二合图，SerialRank（激发了文中提出近端梯度步骤）获得了领先的性能。GNNRank-P 在这里显示的所有合成模型中都表现出色。

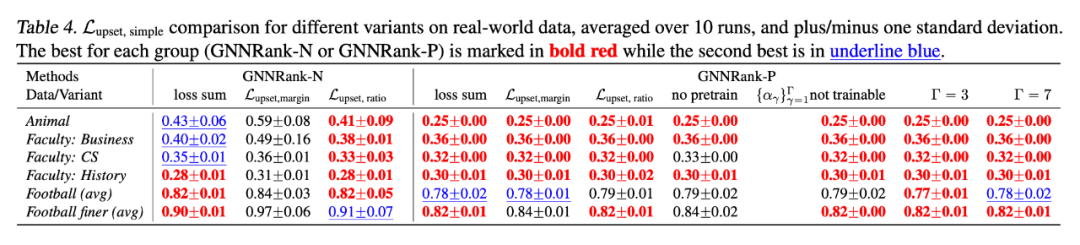
Ablation Study

总结

本文提出了一个基于有向图神经网络的通用框架，用于从成对比较中恢复全局排名。未来的方向包括学习一个更强大的模型来处理不同的输入有向图，在某些约束下最小化干扰，在一些监督真实排名的情况下进行训练，以及探索与低秩矩阵完成的相互作用。以节点级协变量的形式结合辅助信息，并与目前相当有限的现有关于协变量排名的文献进行比较，这是另一个有趣的方向。

更多阅读