集成树之玩转借贷俱乐部

斯蒂文用决策树预测了借贷俱乐部里面的贷款的良恶性，老板比较满意，但是还想进一步提高预测准确率。斯蒂文第一反应是用集成树 (ensemble trees)，比如随机森林和提升树，本贴分三个步骤：

• 预处理数据
  

• 先用 sklearn 自带的梯度提升树 (gradient boosted tree) 和随机森林 (random forest) 模型

• 然后自己编写逐步提升树桩 (adaBoost stump) 模型

预处理数据步骤和在上贴决策树之玩转借贷俱乐部里面做的一模一样，包括三个子步骤：

• 平衡样本 (sample balancing)

• 特征子集 (feature subset)

• 独热编码 (one-hot encoding)

因此本帖不会重复上贴的预处理数据的子步骤，除非有新的内容有所变动或需要强调。

进入王的机器公众号，在对话框回复 ML15 可下载代码 (ipython notebook 和 HTML 格式) 和数据 (csv格式)

目录

第一章 - 集成树 (sklearn)

    1.1 预处理数据

    1.2 提升树和随机森林

    1.3 树的棵数

第二章 - 提升树 (MM)

    2.1 子函数

    2.2 权重树

    2.3 逐步提升树桩

下面斯蒂文用 ipython notebook 带你们继续玩转借贷俱乐部。

第一章：集成树 (sklearn)

1.1

预处理数据

本帖需要用到 numpy, pandas, matplotlib 和 sklearn 这四个是最常见的工具包，分别处理数组运算、数据表操作、绘图和机器学习。 此外还需用到 sklearn 里面三个子模型：

• model_selection 里的 train_test_split 用来划分训练和测试集

• tree 里的 DecisionTreeClassifier 用做普通决策树

• ensemble 里的 RandomForestClassifier 用做随机森林

• ensemble 里的 GradientBoostingClassifier 用做梯度提升树

---

在用 sklearn 自带模型中，我们选取以下 24 个特征 (原来有 67 个特征)，包括评级、子评级、工作年数、房屋所有权、负债收入比、贷款目的、违约次数、贷款利率、年收入、月供等等。

---

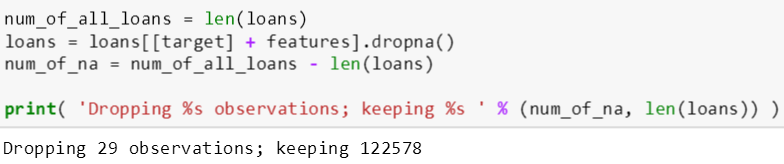
斯蒂文担心 csv 文件会有缺失数据，如果存在，它们会由 pandas 转成 NA 形式，因此他用 dropna() 函数来删除 NA 值。之后斯蒂文又怕有太多 NA 值，那么直接删除大量的数据显示不是一个好的处理方案，因此他检查了删除含 NA 的数据的个数只有 29 个，而剩余的数据个数为 122,578 个。谢天谢地，直接删除它们对最后结果没有什么影响。

---

接下来，和决策树之玩转借贷俱乐部处理方法一样，斯蒂文将整个贷款数据做了平衡化让良性贷款和恶性贷款数目一样，再用独热编码把分类字符型变量转换成 0/1 数值型变量。在本次选取的特征中，只有评级、房屋所有权和贷款目的三个是分类字符型变量。

1.2

提升树和随机森林

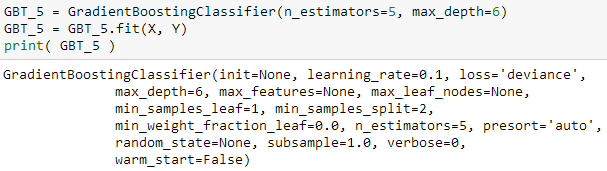
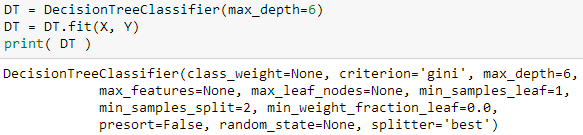
斯蒂文用

• GradientBoostingClassifier 函数来建立提升树模型 GBT_5

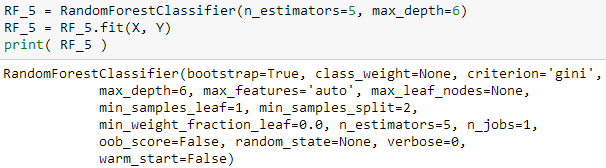
• RandomForestClassifier 函数来建立随机森林模型 RF_5

这两个模型都将树的个数 (n_estimators) 和最大树深 (max_depth) 分别设成 5 和 6。然后用 fit() 函数来拟合 X 和 Y 生成树模型。上面两个函数括号里的变量都可以赋予不同的值，斯蒂文此时就只想通过

• 变化 n_estimators 来控制树的个数

• 变化 max_depth 来控制树的复杂程度

---

为了比较它们和普通树的预测性能，斯蒂文也用 DecisionTreeClassifier 函数来建立一棵普通树，其中 max_depth 也设为 6。

---

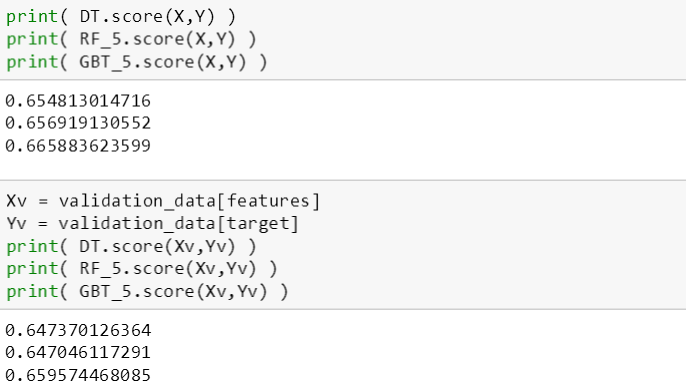
接下来看看这三棵树在训练数据和验证数据上的表现，即检查训练误差和验证误差 (直接用 score 函数来检查准确率，误差 = 1 - 准确率)：

可以看出从验证准确率来看，提升树大于普通树大于随机森林；从训练准确率来看，提升树大于随机森林大于普通树

    验证:  0.6596 > 0.6473 > 0.6470 

    训练:  0.6659 > 0.6569 > 0.6548

综合看出，提升树表现最好，虽然只有 0.01 的提升。但是在 Kaggle 竞赛，这种提升都能压倒不少人呢，关键是从 sklearn 里面用 GradientBoostingClassifier 和用 DecisionTreeClassifier，没费任何力气，模型性能就得到了提高。说点题外话，一般在 Kaggle 进 10% 的选手都会使用梯度提升树，确切来讲，他们都使用极度梯度提升树 (XGBoost)。 

---

随机森林虽然预测准确率没有提升树好，但是它有个非常厉害的地方，可以做特征选择，具体方法可参考随机森林和提升树一贴。代码展示如下：

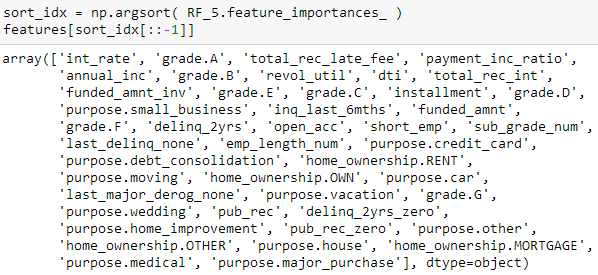
1. 首先按原来特征顺序用 feature_importances_ 获得它们的权重

2. 再用 argsort() 找到排序对应的索引 sort_idx，默认为升序排列，也就是最后面的特征越重要

3. 最后反向打印出特征，发现 int_rate, grade.A, total_rec_late_fee是三个最重要的特征

---

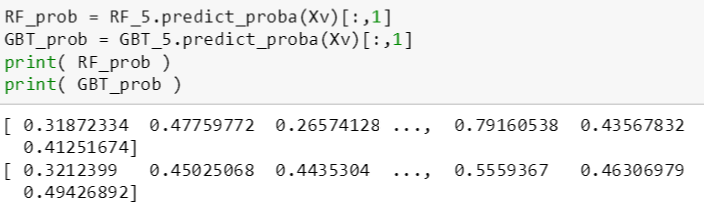
接下来，斯蒂文想看最安全和最危险的 5 笔贷款的评级，模型哪个指标能反映出安全或危险的程度呢？答案是 predict_proba 函数。

它接受经过独热编码后的数值类贷款数据表 (n 行)，返回出一个概率数组 (n 行 2 列)，第 1 列指的是正例的概率，第 2 列指的是反例的概率。通常惯例是需要关注的例子当做正例，那么在我们的贷款问题中，危险贷款是需要关注的，因此是正例，对应着概率数组的第 1 列；而安全贷款对应着概率数组的第 2 列。注意我们用 [:,1] 取的第 2 列，因此概率值越大贷款越安全，越小贷款越危险。  

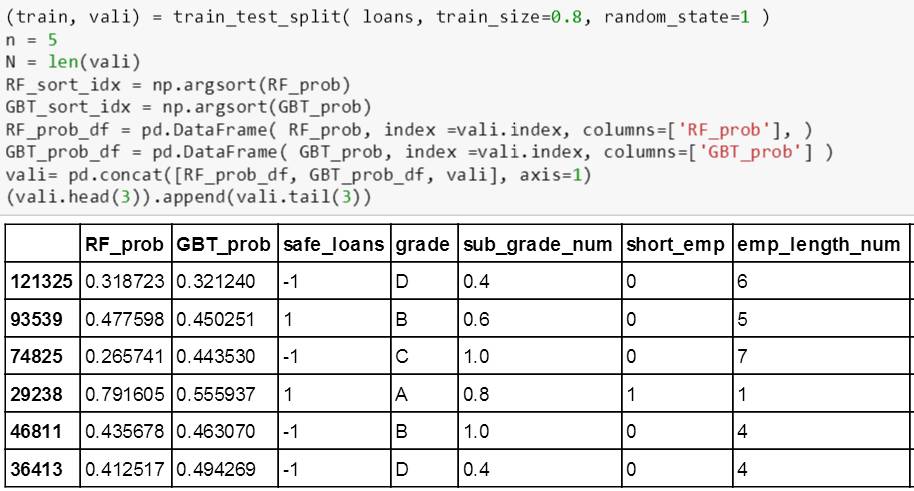
之后将 RF_prob, GBT_prob 和验证数据 vali 合并成一个新的数据表，并用 argsort() 找到排序对应的索引 RF_sort_idx 和 GBT_sort_idx。

举个例子，对于[10 5 7] 排升序，应该为 [5 7 10]，那么对应升序的索引为 [1 2 0]：排在第一位的 5 原来索引为 1，排在第二位的 7 原来索引为 2，排在第三位的 10 原来索引为 0。

根据索引里面的值，可以很容易得找到前 5 笔 (top negative) 和后 5 笔 (top positive) 的贷款评级 (因此概率按升序排，越大的概率对应着贷款越安全，排在越后)。

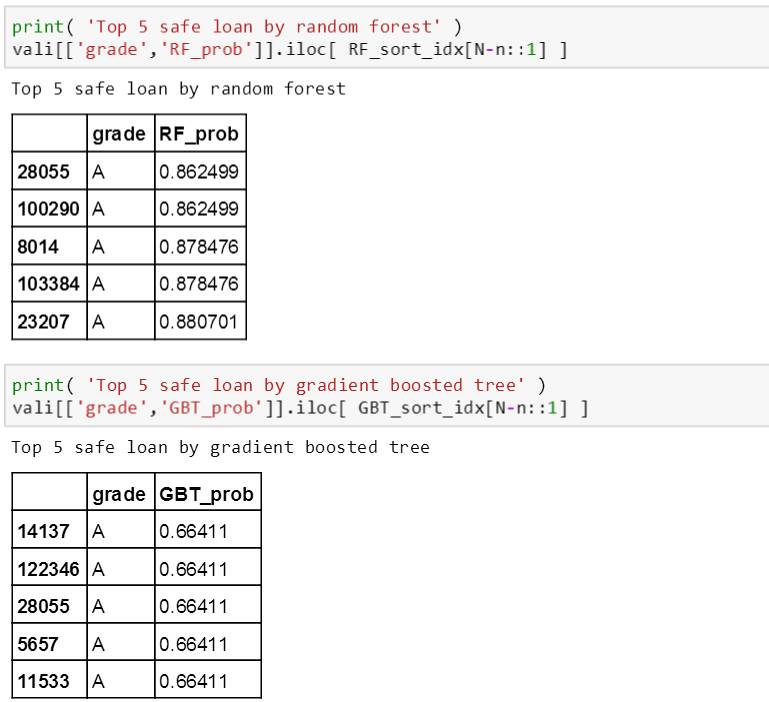
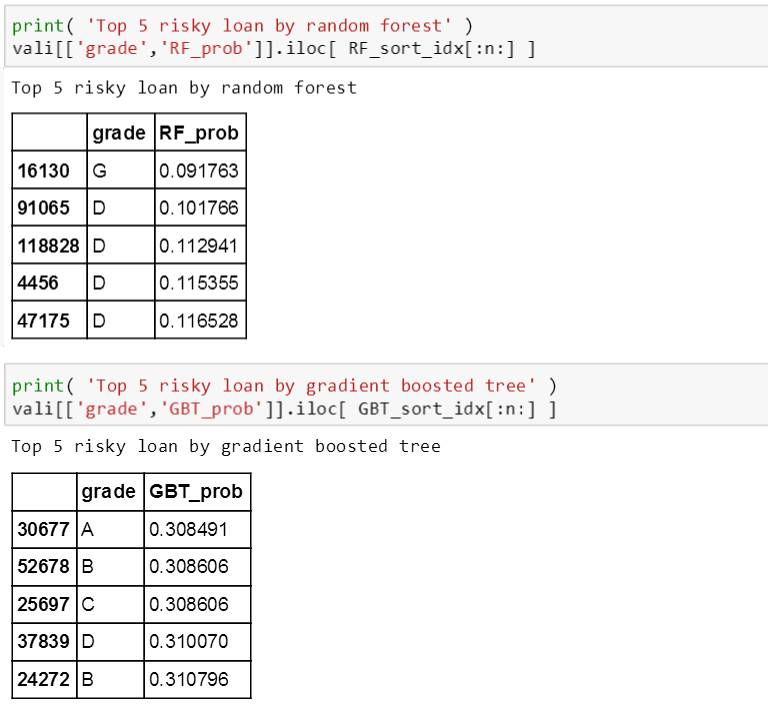
分别在随机森林和提升树模型下打印出最安全和最危险的 5 笔贷款的评级和概率，如下：

从上面结果发现两个特点：

1. 随机森林生成的概率范围 [0.092, 0.881] 比提升树生成的 [0.308, 0.664] 宽很多

2. 在最安全的 5 笔贷款中，两个树模型预测的贷款都是 A 评级，比较合理；但是在最危险的 5 笔贷款中，随机森林预测的贷款有 D, G 评级，而提升树预测的贷款居然还有 A 评级 (不是那么合理)

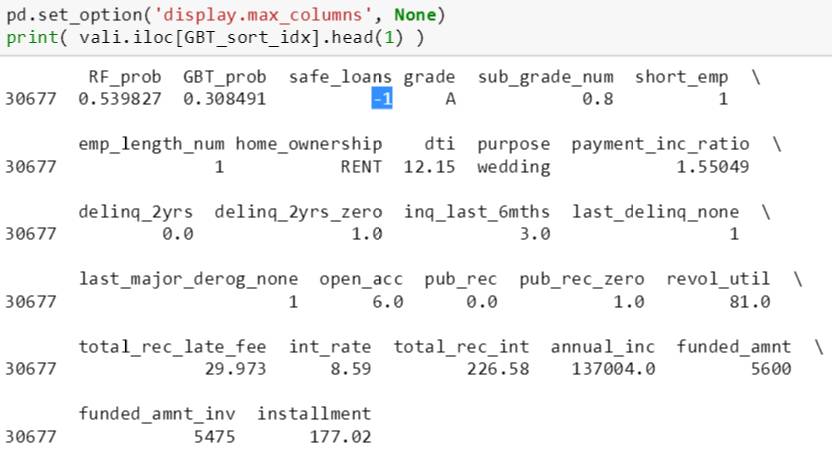
斯蒂文继续往下挖，打印出这个 A 评级的贷款所有信息，如下：

尽管评级为 A，这笔贷款还是被人为分成恶性贷款，见上图蓝色高亮部分的 -1。和其他良性贷款相比，查了查原因可能是迟交款项 (total_rec_late_fee) 29.973 太高，或者负债收入比 (dti) 12.15 太高，或者过去六个月被债权人询问 (inq_last_6mths) 3 次太多。这个有兴趣的同学可以自己继续深挖以下，虽然评级为A，但提升树可能也将其他特征综合考虑而将其分类为恶性贷款。

1.3

树的棵数

随着树的棵数增加，斯蒂文想看看随机森林和提升树模型性能怎么改进，因此对每个模型训练了 5 次，树的棵数分别设为 10, 50, 100, 200 和 500，最大树深还是设为 6。

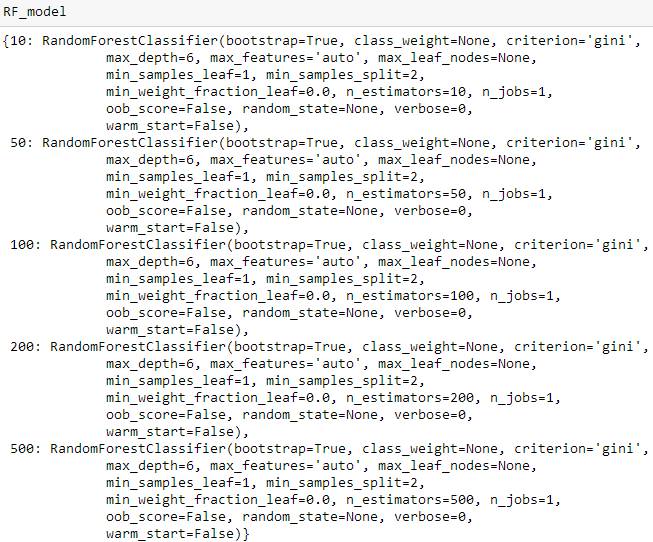
将随机森林和提升树模型打印如下：

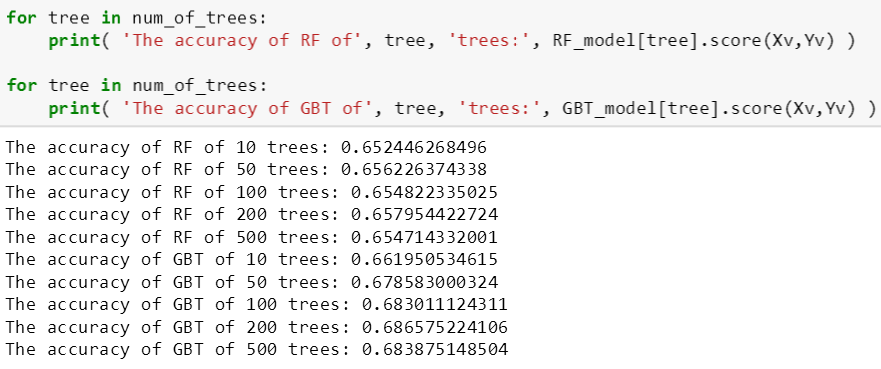
之后用 score() 计算每个子模型的验证准确率，斯蒂文发现其准确率也不是随树的棵数增加而增加的，比如 RF 和 GBT 都是在 100 棵数时验证准确率最大，到 500 棵数时验证准确率反而还会降低。

图永远比数字直观，下面 make_figure 函数就是一个通用的画图框架，使用者可以自由定义其维度、标题、横轴标记、纵轴标记和标注。

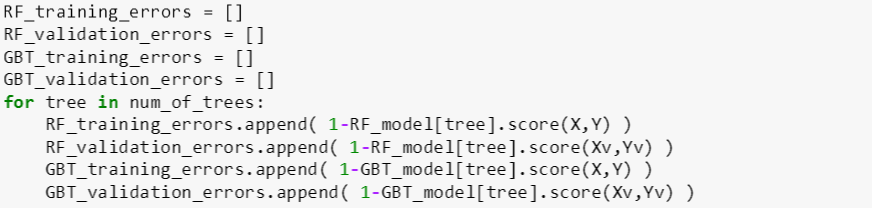
循环算出 RF 和 GBT 在每个子树集上的训练误差和验证误差，最后展示在一幅图里。

从上图看出，绿线 (GBT 训练误差) 一致低于蓝线 (RF 训练误差)，而且红线 (GBT 验证误差) 一致低于黄线 (RF 验证误差)，因此 GBT 比 RF 预测性能好。

注：本章可参考 MM - ensemble trees 的 ipython notebook

第二章：提升树 (MM)

2.1

子函数

本章还是需要用到 numpy, pandas, matplotlib 和 sklearn 这四个工具包。 此外还需用到 sklearn 里model_selection 里的 train_test_split 用来划分训练和测试集。

---

本章只用评级、年限、房屋所有权和工作年数这四个特征对贷款是否良性恶性做决策。

---

count_weighted_mistakes 函数有两个输入变量：

• labels_in_node: 标签样例值 (数组)

• data_weights: 数据权重 (数组)
  

其代码逻辑分两步：

1. 计算结点里面正例和反例的权重总数

2. 根据多数原则

1. 如果正例权重总数大于反例权重总数，那么反例是误分类则返回反例权重总数和正类

2. 如果正例权重总数小于反例权重总数，那么正例是误分类则返回正例权重总数和反类

本帖 count_weighted_mistakes 是上贴 count_num_mistakes 延伸版，后者计算样例误分类而前者计算权重样例误分类，前者把 data_weights 里面的元素全部设为 1 就是后者。

---

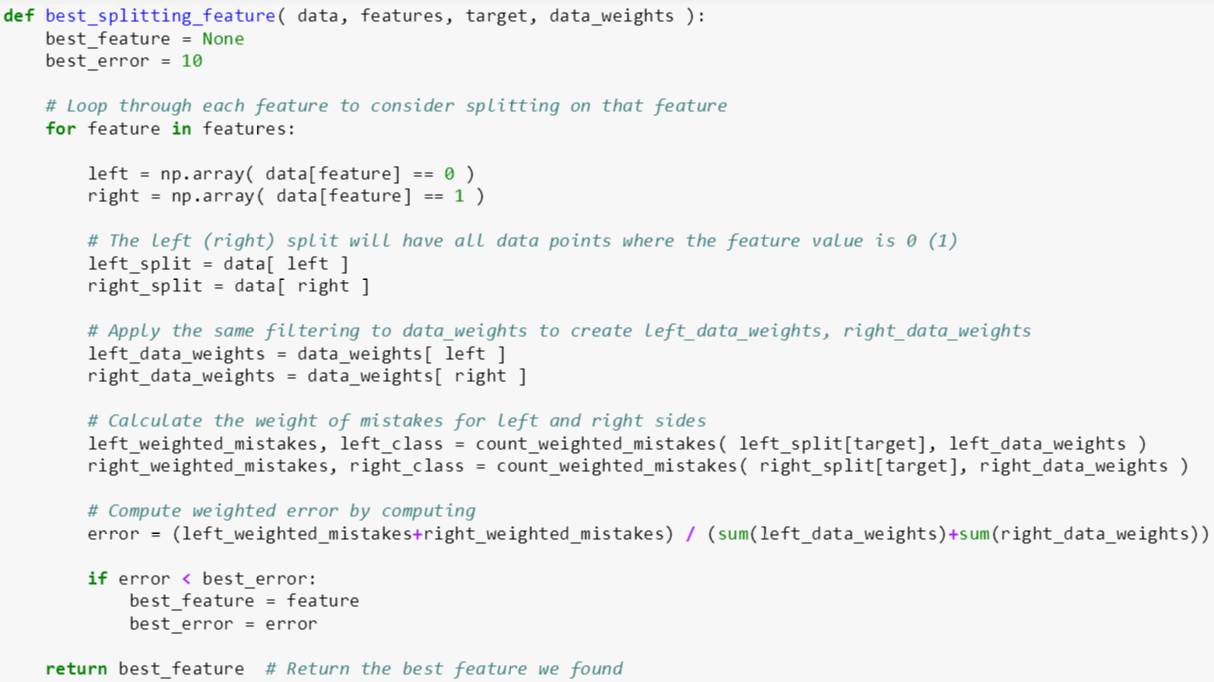
best_splitting_feature 函数有四个输入变量：

• data: 某棵树 [数据表]

• features: 特征名称 [数组]

• target: 标签 [字符]

• data_weights: 数据权重 (数组)
  

其代码逻辑分四步：

1. 初始化最佳特征和最佳误差率分别为 None 和 10
   

2. 对于每个特征 j，计算用其分裂的左子树和右子树的权重误分类数 (用 count_weighted_mistakes)，并计算权重误分类率 j

3. 如果权重误分类率 j 小于最佳误差率，那么最佳误差率为权重误分类率 j，而最佳特征为特征 j

4. 重复运行第二、三步，最后返回最佳特征

本帖 best_splitting_feature 是上贴写的延伸版，后者计算误分类率而前者计算权重样误分类率，前者把 data_weights 里面的元素全部设为 1 就是后者。

---

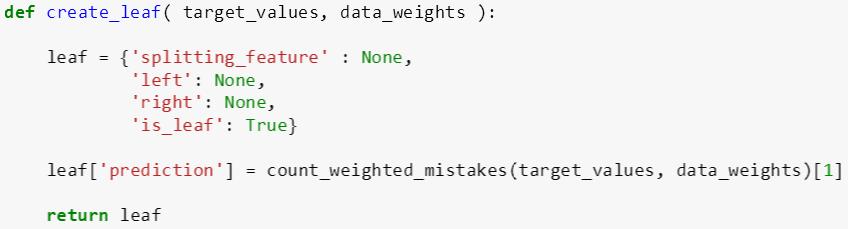
create_leaf 函数有两个输入变量：

• target_values: 标签样例值 (数组)

• data_weights: 数据权重 (数组)
  

其代码逻辑分两步：

1. 用字典类变量初始化 leaf，它的分裂特征为 None, 左子树为 None, 右子树为 None, 是否是叶子为 True 

2. 利用 count_weighted_mistakes ，赋值 leaf 的预测为 1 (正例权重总数大于反例权重总数)，-1 (反例权重总数大于正例权重总数)

注意代码倒数第二行有个索引 [1]，这是因为 count_weighted_mistakes 返回值有两个，第一个是权重总数，第二个是类，这里需要第二个返回值。同样本帖 create_leaf 是上贴写的延伸版，前者把 data_weights 里面的元素全部设为 1 就是后者。

---

利用上面三个子函数，斯蒂文可以很轻松的构建权重树模型，同时使用以下三个停止条件：

• 条件 1 - 某分支里所有样例都属于一类

• 条件 2 - 特征已经用完

• 条件 3 - 树的深度达到最大树深

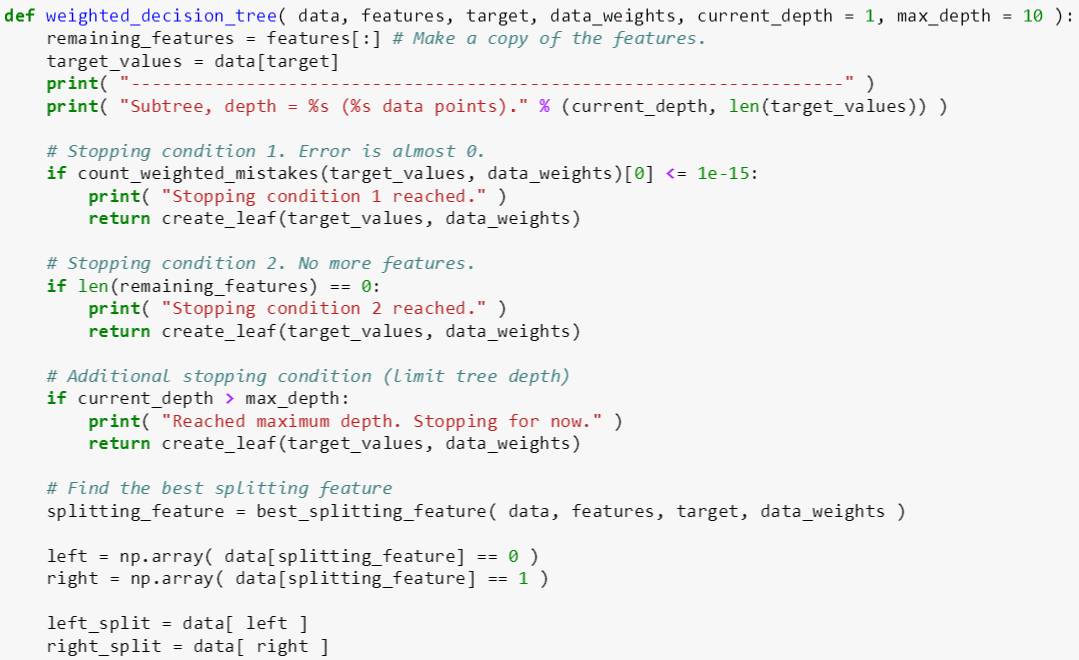
weighted_decision_tree 函数有六个输入变量：

• data: 某棵树 [数据表]

• features: 特征名称 [数组]

• target: 标签 [字符]

• data_weights: 数据权重 (数组)
  

• current_depth: 当前树深 [整数]

• max_depth: 最大树深 [整数]

其代码逻辑分三步：

1. 创建 remaining_features 包含所有特征

2. 检查三种停止条件：

1. 如果权重误分类总数 (用 count_weighted_mistakes) 小于 10-15，创建叶子 (停止条件 1)

2. 如果特征已用完，创建叶子 (停止条件 2)

3. 如果 current_depth 小于 max_depth，创建叶子 (停止条件 3)

3. 用 best_splitting_feature 找到最佳特征，并分裂成左子树和右子树，同时将最佳特征从 remaining_features 删除

1. 如果左子树或右子树所含样例个数等于父树所含样例个数，那么创建叶子

2. 反之，用递推方法继续用 weighted_decision_tree 来创建子树，这时 current_depth 在原来基础上加 1

本帖 weighted_decision_tree 是上贴 decision_tree 延伸版，前者把 data_weights 里面的元素全部设为 1 就是后者。

2.2

权重树

非权重树

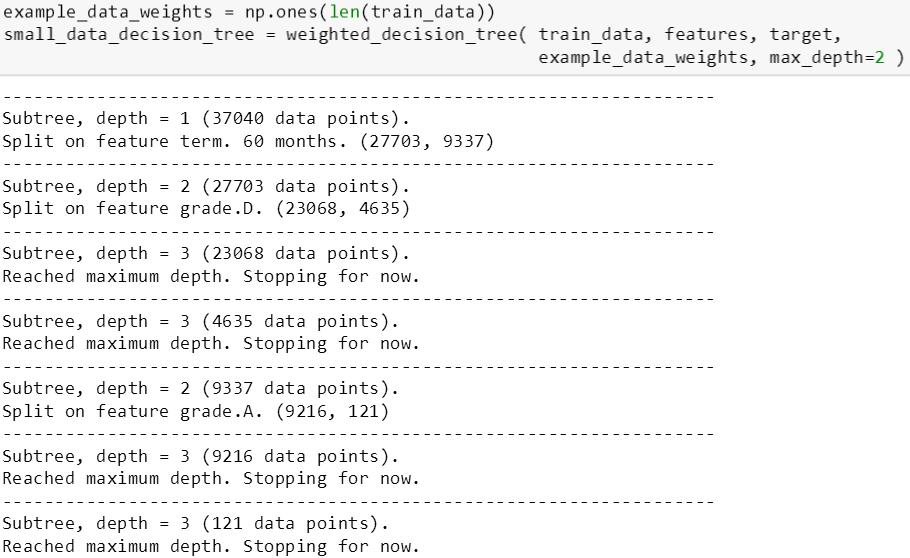
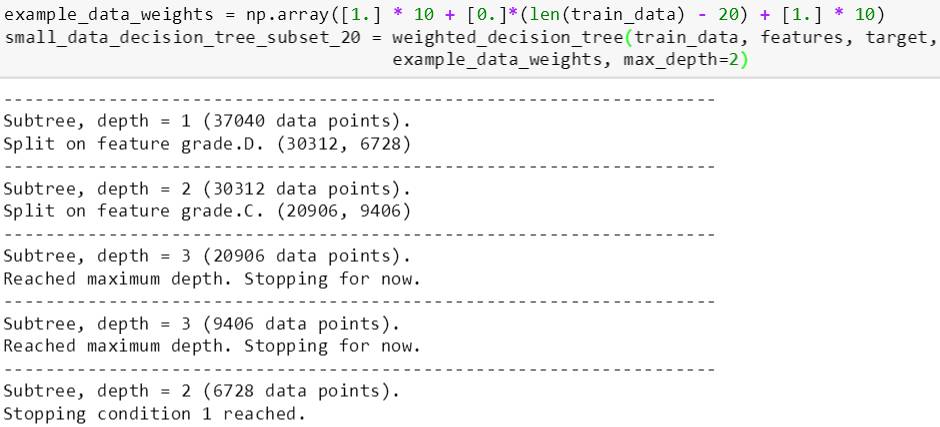
将 max_depth 设为 2，斯蒂文首先用上面程序训练了一棵数据权重相同的树 (权重全部设为 1)，每步分裂结果如下：

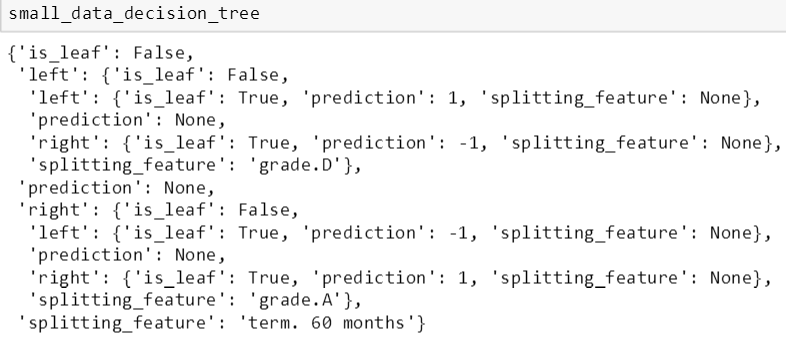
将这个树的结构打印出来得知，它首先在 term.60 months 做分裂，左子树在 grade.D 做分裂得到叶子，而右子树在 grade.A 做分裂得到叶子。

用上贴写好的 misclassify_error 函数计算出这棵非权重树的测试误差为 0.4059。

权重树

接着斯蒂文再训练了一棵权重树 (前后 10 个权重全部设为 1，中间都是 0)，每步分裂结果如下 (max_depth 仍设为 2)：

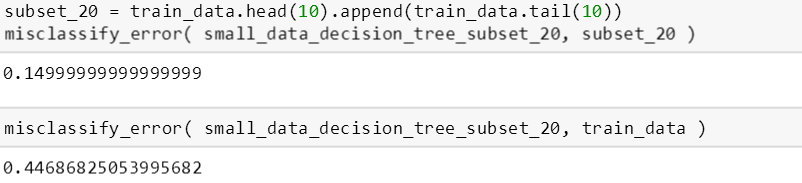
下面看看这棵权重树在 subset_20 (权重放 1) 的训练误差，只有 0.15，但是该树在整个训练集上的误差高达 0.4468。

subset_20 里的数据权重为 1，而其他数据权重都为 0，因此前者比后者更重要，在训练的时候也更受重视；而后者在训练中完全被忽视了。等等，这套理念不是很像逐步提升 (adaBoost) 么？

2.3

逐步提升树桩

adaboost_tree_stumps 函数有四个输入变量：

• data: 某棵树桩 [数据表]

• features: 特征名称 [数组]

• target: 标签 [字符]

• num_tree_stumps: 树桩个数 [正整数]

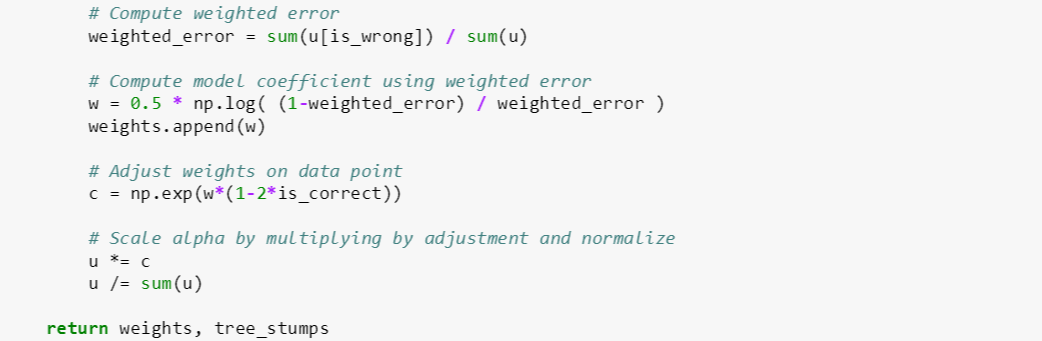
其代码逻辑参考随机森林和提升树一贴的 adaBoost 非常容易看懂。对照下图，adaboost_tree_stumps 主要完成了步骤 1 到 3 而最后得到了 num_tree_stumps 个树桩和对应的权重 (注意这里的权重是每个树桩配给的权重，不要和上面数据的权重弄混淆)。

上图最后的非均匀组合由下面的 predict_adaboost 代码实现 (代码里面的函数 classify 和上贴的一样)：

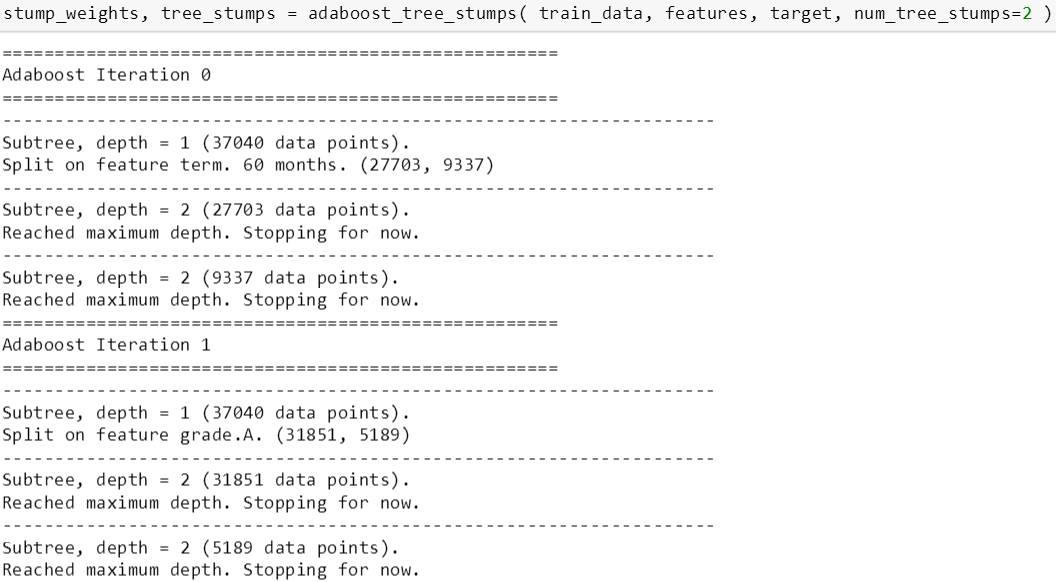
两个树桩

首先斯蒂文先从最简单的 2 个树桩开始，看看那些它们用到哪些特征来分裂树桩，同时也可以测试一下上面的代码是否运行正常。由下图可知，第一个树桩用 term.60 months 来分裂，而第二个树桩用 grade.A 来分裂。

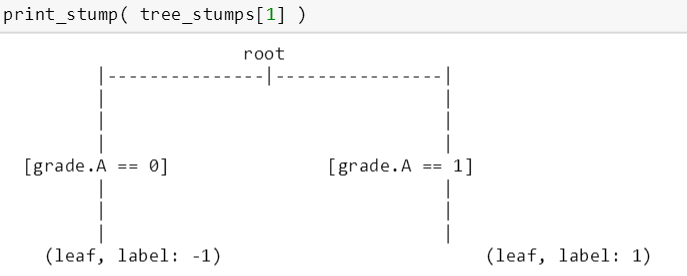
用上贴的 print_stump 函数打印这两个树桩。

而它们对应的权重为

多个树桩

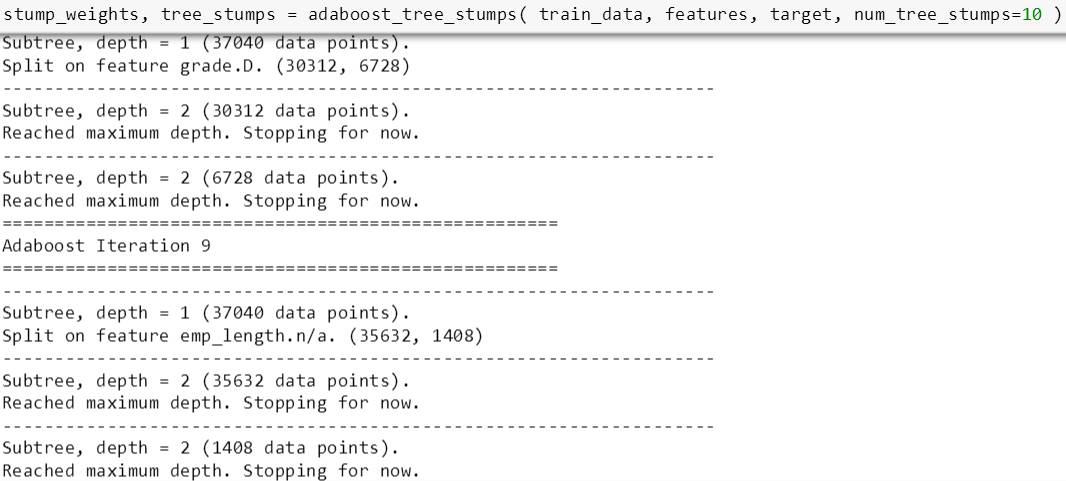
接下来斯蒂文用多个树桩来看看 adaBoost 的预测能力。先试试 10 个树桩：

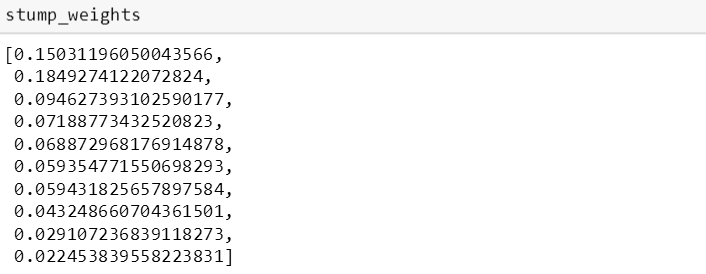
将 predict_adaboost 用到测试数据得到预测值，并和真实值比较算出测试准确率 0.61，并且打印出这 10 个树桩对应的权重，发现权重几乎是逐渐递减的。

斯蒂文接着再试试 30 个树桩：

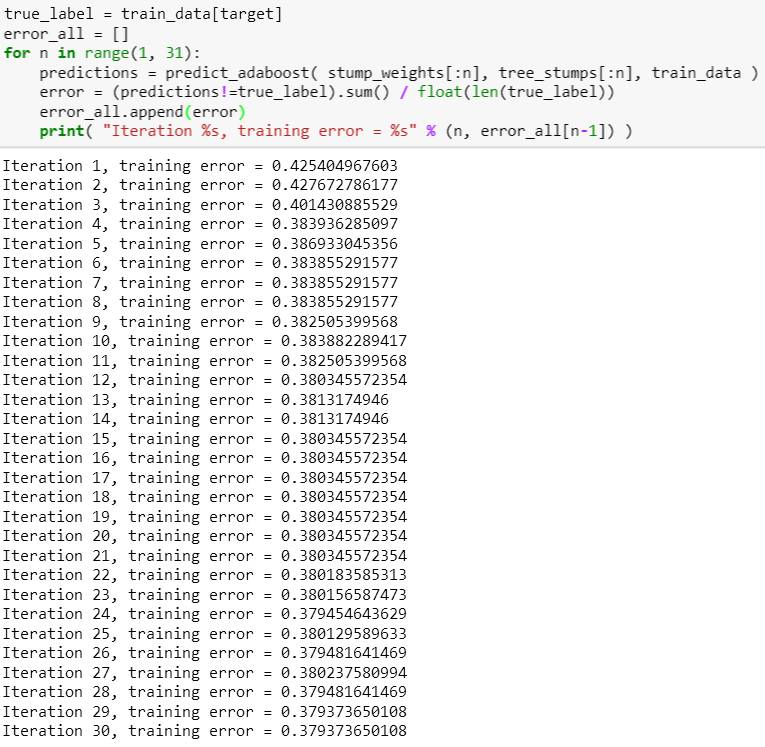
现在他想看看在树桩个数增多时，模型的训练误差如何变化。最直观的方法是在每前 n 个树桩上计算一个误差，存在一个 list 里面，最后展示在图上。

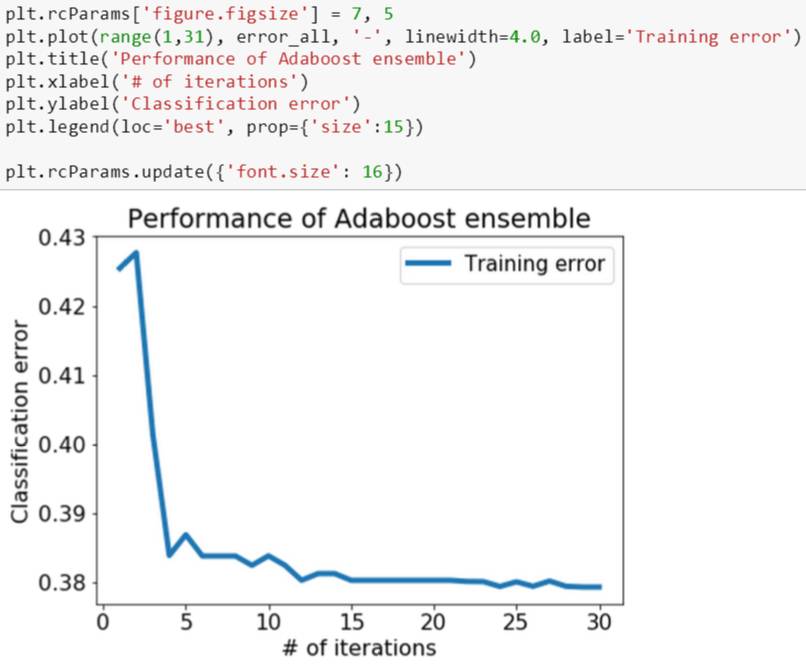
由下图看出，训练误差随着树桩数增加而减少，在前 5 个树桩尤为明显，后面减少的幅度低了很多，因此在本例选择树桩数时，根本没必要选到 30 这么多，具体多少个要看你对误和计算时间的容忍度而权衡决定。

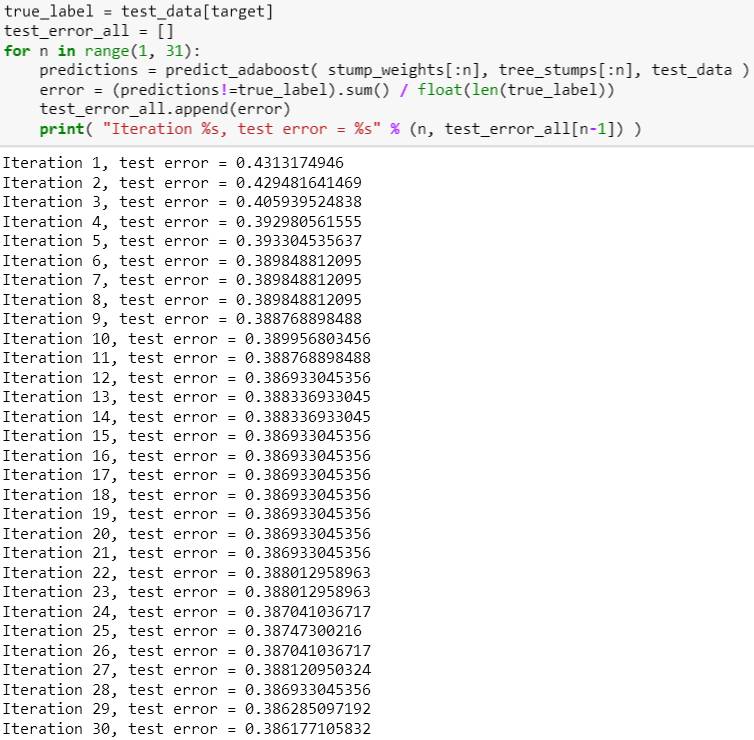
训练误差的趋势研究完了，最重要的是看测试误差，因为这个才是评估模型未来泛化能力的指标。和训练误差一样，在每前 n 个树桩上计算一个测试误差，存在一个 list 里面，最后将训练和测试误差都展示在一张图上。

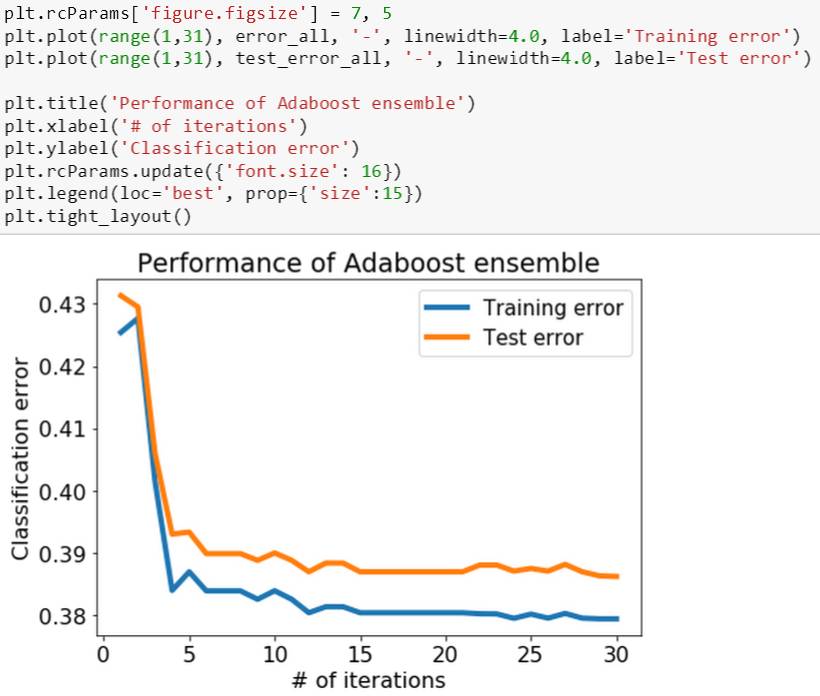
由下图可知，训练和测试误差的趋势很像，但是测试误差总是比训练误差略大一些，这也非常合理因为模型是在训练数据上做的。最重要的是，测试误差没有随着训练误差一直减小而在某点突然增大，因此这个 adaBoost 模型没有明显的过拟合。

注：本章可参考 MM - boosting 的 ipython notebook

下帖开始讲机器学习理论 (Machine Learning Theory)，吴恩达曾经在斯坦福机器学习 CS229 课上讲过

懂得机器学习理论是区分只知道从书本中死读机器学习的人和在实践中当模型结果不满意时知道如果如何改进的人。

很明显，我想成为他说的后者，因此也花了不少功夫在机器学习理论上。下一章对数学要求比较高，对我的要求也就更高，因为我要让那些非数学专业的人把机器学习理论弄懂！ Stay Tuned！