在数据处理过程中用好概率论

前提

在数据处理过程中用好概率论

郭朝晖 | 文

        假设

                                                 独立同分布 

不确定性

开 篇

原文自【蝈蝈创新随笔】,已获郭老师授权, [遇见数学]特此感谢支持!

郭朝晖

郭朝晖博士，教授级高工，宝钢中央研究院首席研究员。曾担任中国工业与应用数学学会常务理事、副理事长。

南开大学有位老先生，认为所有的数据建模方法可以分成两类：一类是基于概率论的，一种不是基于概率论的。这个观点非常独到：基于概率论的方法有个好处，只要前提和假设条件成立，结论一定是正确的；而另外一种则不需要考虑前提是不是正确——当然，结论的可靠性也就差了一点。做工业大数据分析的人，特别希望得到可靠的结果。这就会让我们倾向于前者。但却一直面临“前提条件”的困惑。该怎么办呢？在我看来，吴老师的分类其实已经给出了方向：我们认识到了两类方法的割裂，就应该反其道而行之，走两者结合的路子。但如何结合呢？要从研究这些“前提条件”入手。本文就是基于这种思路下的思考。我很多年没搞理论研究了。这些思考不一定对，欢迎批评指正。

数学被称为自然科学之母。数学往往可以非常好地描述自然世界及其规律，这是数学理论与自然实际相结合的基础。数学模型往往如此之精准，以至于人们会习惯性地把自然规律和数学模型等同起来、难分彼此。比如，把现实中的点、线、面看做几何学中的点、线、面。我们知道，从非欧几何从产生之日起，都难以被非专业人士理解。一个重要的原因就是：人们往往把描述欧式空间的数学模型和真实的物理空间本身混问一谈了。

两人分列东西，沿着两条平行线向正南方走。他们会不会交会呢？欧氏几何的回答是：不会；非欧几何的回答是：相交在南极。

 

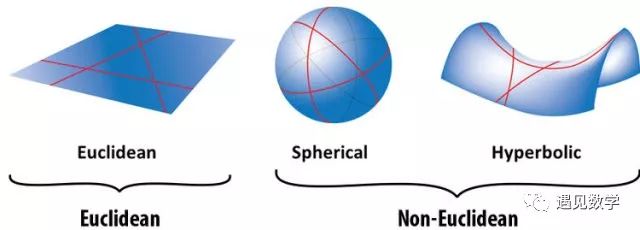
尽管数学模型可以无限逼近真实世界，但却是两个不同的体系。事实上，对同样一个客观对象，我们可以给出不同的描述方法、同样准确地描述客观世界——就像用笛卡尔坐标系和极坐标系可以描述同样的物理空间一样，他们就像从不同的侧面给人照出的相片。事实上，当虚数、δ函数等现实中不存在的东西，也成为数学体系中的组成部分后，人们就应该认清数学模型的世界和现实世界是两码事。换句话说：数学只是用来描述自然界及其运行规律的工具，而不是自然界或运行规律本身。

 

既然是两码事，有个问题就是天然存在的：数学模型和自然界差别到底有多大？我们在应用概率理论的时候，这个问题显得特别重要：稍一不慎，模型就会出现巨大的偏差。

30年前，当我还是个懵懵懂懂的学生时，问概率老师、范大茵教授一个奇怪的问题：“我们知道，男女孩出生比例一般是51.2:48.8。假设我们用了两种统计方法：一种是把全国的数据放在一起计算，得到这个结果；另一种是各个省市分别计算，都得到相同的结果。请问两种结果是否给出了同样多的信息？”。范老师的回答是：“如果人口出生是独立同分布的，两个统计方法的信息量就是一样的。” 凑巧的是：此后的若干年，由于出现了选择性生育，中国新出生人口的比例常常在54:46左右，各个省市也不一样。所以，“人口出生是独立同分布”只是一种假设。这种假设，在原始的自然条件下成立，在人为干扰下就不再成立了。

 

30年过后，我对范老师的回答，有了更深刻的理解：要把现实中的一件事看成概率问题，是要有前提条件的。数学中的概率，要受规律的约束，而现实中的事件则未必受这种约束。把概率论应用到现实中，真的要当心！

概率论是数学的一个分支。随着数据处理技术越来越热，应用也越来越广泛了。在我看来：在描述实际问题时，概率论的“滥用”是个非常值得关注的问题。所谓的“滥用”，就是不认真考虑对象是否适合用概率来描述，就直接套用相关做法和结论了。

 

概率论为什么特别容易被滥用呢？这要从“不确定性”谈起。

 

我们每天面对大量的不确定性。但概率理论中讲的“不确定性”是有前提条件的、背后有确定性的要求。例如，单个事件的发生是不确定的，但概率分布却是确定的。概率分布确定了，很多相关指标（如期望、方差等等）也就确定了。自然界中不确定性的事件很多，但有些不确定性是不受统计分布约束的，不一定适合用概率描述。

其实几何学也是一样：数学上“直线”的概念可以用来较好地描述桌子的边沿，却不一定适合描述弯曲的河流。

例如，用概率理论的时候，我们常常不自觉地假设样本符合独立同分布的条件。但是，这种假设在现实中常常是不成立的。比如，企业产品缺陷的发生率，可能与产品种类、原材料质量、设备状态、质检要求有关，缺陷发生率并不稳定。换句话说，我们往往需要对样本的来源加以规范，才有可能保证“独立同分布”的条件。但这是要花很大工夫的：因为我们可能根本不知道哪些因素影响这个条件的成立。

 

概率和统计常常被人联系在一起，并称为“概率统计”。其实，没有概率理论，照样可以有统计学方法。但是，有了概率理论，可以让统计方法的理论基础更加扎实，成为真正的数学方法，使用过程的可靠性也更高。然而，如果滥用概率的相关概念，统计学的这一优势（与现在一些数据建模方法相比）也就丧失了。

统计回归是我最常使用的方法。在我看来，回归的本质是：针对某类对象，研究不同属性之间的函数关系。人们一般会注意到后半句——即研究属性之间的关系（也就是建模）。但是，人们却常常忽视前半句“某类对象”,也就是定义概率所依据的特定样本空间。前半句的重要性在于：我们针对的类别不同，属性之间的关系是不一样的。例如，研究年龄与吸烟的关系时，男性和女性的曲线是不一样的。如果把男女放在一起计算，曲线会介于两者之间，并随着男女比例的变化而上下浮动。这就意味着：如果不固定男女比例，就得不到稳定的曲线，研究也就不能算成功。

 

用概率论指导统计工作，就要学会认真对待样本空间。20年前我刚到宝钢的时候，我的师傅王洪水先生就对我讲起老外的观点：“会搞统计的人，是那些善于凑数据的”。也就是说：善于选择样本空间，让空间中的“规律”稳定——这就是让对象或过程的某些不确定性尽量减少。反之，那些整天只对着固定的样本空间修改算法的人，很可能是在“缘木求鱼”：数据混在一起就没有稳定的规律了，怎么可能找得到呢？

尽管不同集合里面的规律不一样，但有时可以统一起来。比如我常说的，用非线性关系统一不同的线性关系。但这话就太长了，不展开了。

总结一下：概率论研究的是不确定性，却要求有确定性的先验条件；数据建模面对的是具有不确定性的对象或过程，而我们的目标却是追求确定性、降低和控制不确定性。认识到这些矛盾，才能把数据分析工作做好。

(完)

图自网络

「予人玫瑰, 手留余香」

与朋友分享阅读好文乐趣!