可视化理解二值交叉熵/对数损失

极市导读
损失函数通常用来评价模型的预测值和真实值不一样的程度,损失函数越好,通常模型的性能越好。本文主要以清晰简洁的方式解释了二值交叉熵/对数损失背后的概念。 >>加入极市CV技术交流群,走在计算机视觉的最前沿
介绍
如果你正在训练一个二分类器,很有可能你正在使用的损失函数是二值交叉熵/对数(binary cross-entropy / log)。
你是否想过使用此损失函数到底意味着什么?问题是,鉴于如今库和框架的易用性,很容易让人忽略所使用损失函数的真正含义。
动机
我一直在寻找一个可以向学生展示的以清晰简洁可视化的方式解释二值交叉熵/对数损失背后概念的博客文章。但由于我实在找不到,只好自己承担了编写的任务:-)
一个简单的分类问题
让我们从10个随机点开始:
x = [-2.2, -1.4, -0.8, 0.2, 0.4, 0.8, 1.2, 2.2, 2.9, 4.6]
这是唯一的特征:x
现在,让我们为点分配一些颜色:红色和绿色。这些是我们的标签。
因此,我们的分类问题非常简单:给定特征x,我们需要预测其标签:红或绿。
由于这是二分类,我们还可以提出以下问题:“该点是绿色吗? ”,或者更好的问法,“ 该点是绿色的概率是多少?” 理想情况下,绿点的概率为1.0(为绿色),而红点的概率为0.0(为绿色)。
在此设置中,绿点属于正类(是,它们是绿色),而红点属于负类(否,它们不是绿色)。
如果我们拟合模型来执行此分类,它将预测每个点是绿色的概率。假定我们了解点的颜色,我们如何评估预测概率的好坏?这就是损失函数的全部目的!对于错误的预测,它应该返回高值,对于良好的预测,它应该返回低值。
对于像我们的示例这样的二分类,典型的损失函数是binary cross-entropy / log。
损失函数:二值交叉熵/对数(Binary Cross-Entropy / Log )损失
如果您查看此损失函数,就会发现:

其中y是标签(绿色点为1 , 红色点为0),p(y)是N个点为绿色的预测概率。
这个公式告诉你,对于每个绿点(y = 1),它都会将_log(p(y))添加_到损失中,即,它为绿色的对数概率。相反,它为每个红点(y = 0)添加_log(1-p(y))_,即它为红色的对数概率。看起来不难,但好像不大直观……
此外,熵与这一切有什么关系?我们为什么首先要对数概率?这些是有意义的问题,我希望在下面的“ 向我展示数学 ”部分中回答。
但是,在介绍更多公式之前,让我向你展示上述公式的直观表示 ...
计算损失-可视化方式
首先,让我们根据它们的类(正或负)分开所有点,如下图所示: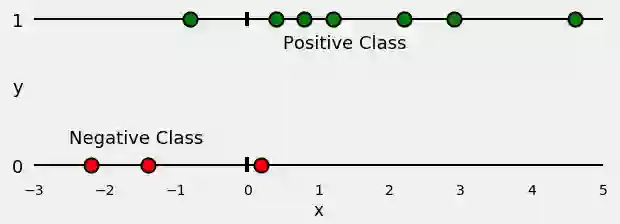
现在,让我们训练一个Logistic回归来对我们的点进行分类。拟合回归是一个sigmoid曲线,代表对于任何给定的x,一个点是绿色的概率。看起来像这样: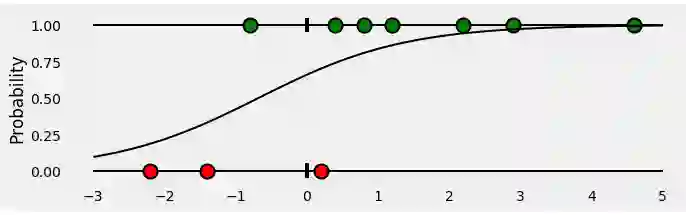
那么,对于属于正类(绿色)的所有点,我们的分类器给出的预测概率是多少?看sigmoid曲线下对应点x坐标上的绿色条。
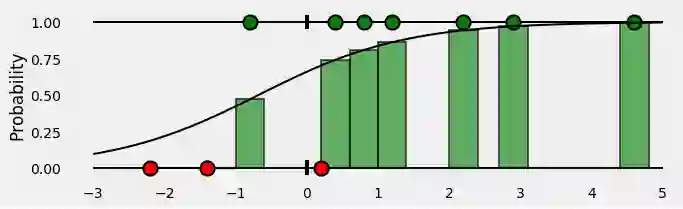
OK,到目前为止还不错!那负类的点又如何呢?请记住,sigmoid曲线下方的绿色条表示给定点为绿色的概率。那么,给定点为红色的概率是多少呢?当然是sigmoid曲线以上的红色条啦 :-)
放在一起,我们最终得到这样的结果: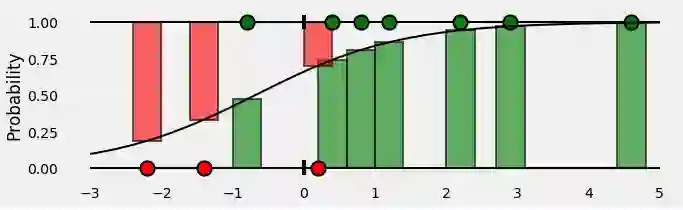
条形图表示与每个点的对应真实类别相关的预测概率!
好的,我们有了预测的概率…是时候通过计算二值交叉熵/对数损失来评估它们了!
这些概率就是我们要的,因此,让我们去掉x轴,将各个方条彼此相邻:
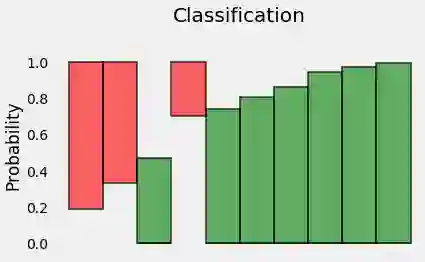
这样,吊起来的方条不再有意义,所以让我们重新定位一下: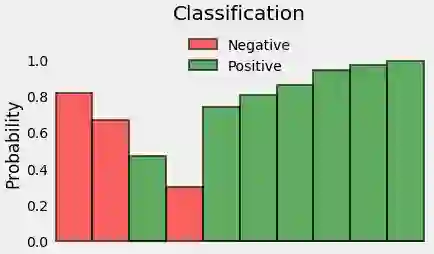
由于我们正在尝试计算损失,因此我们需要对错误的预测进行惩罚,对吧?如果实际的类的概率是1.0,我们需要它的损失是零。相反,如果概率低,比如0.01,我们需要它的损失是巨大的!
事实证明,对于这个目的,采用概率的(负)对数非常适合(由于0.0和1.0之间的值的对数为负,因此我们采用负对数以获得损失的正值)。
实际上,我们为此使用对数的原因是由于交叉熵的定义,请查看下面的“ 告诉我数学 ”部分,以获取更多详细信息。
下面的图给了我们一个清晰的展示 - 实际的类的预测概率越来越接近于零,则损失指数增长: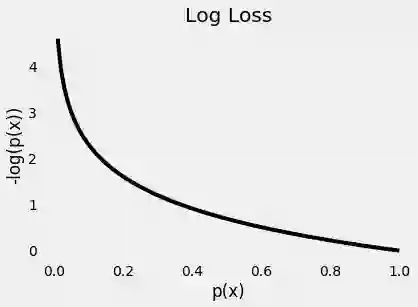
很公平!让我们取概率的(负)log -这些是每个点相应的损失。
最后,我们计算所有这些损失的平均值。
瞧!我们已经成功地计算了这个玩具示例的二值交叉熵/对数损失。是0.3329!
给我看代码
如果你想仔细检查我们得到的值,只需运行下面的代码 :-)
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import log_loss
import numpy as np
x = np.array([-2.2, -1.4, -.8, .2, .4, .8, 1.2, 2.2, 2.9, 4.6])
y = np.array([0.0, 0.0, 1.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0])
logr = LogisticRegression(solver='lbfgs')
logr.fit(x.reshape(-1, 1), y)
y_pred = logr.predict_proba(x.reshape(-1, 1))[:, 1].ravel()
loss = log_loss(y, y_pred)
print('x = {}'.format(x))
print('y = {}'.format(y))
print('p(y) = {}'.format(np.round(y_pred, 2)))
print('Log Loss / Cross Entropy = {:.4f}'.format(loss))
告诉我数学(真的吗?!)
这篇文章并不倾向于从数学上解释……但是对于一些的读者,希望了解熵,对数在所有方面的作用,好, 我们开始吧:-)
分布
让我们从点的分布开始。y代表我们点的类别(我们有3个红点和7个绿点),这是它的分布,我们称其为q(y),如下所示: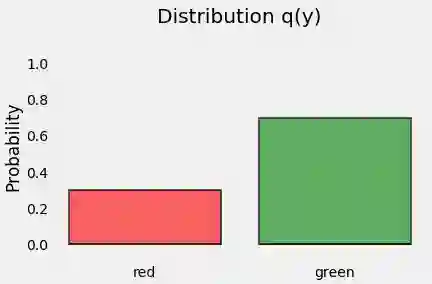
熵(Entropy)
熵是一个与给定的分布q(y)相关的不确定性的量度。
如果我们所有的点都是绿色的,这种分布的不确定性是什么?零,对吗?毕竟,毫无疑问,点的颜色:它总是绿色!因此,熵为零!
另一方面,如果我们确切知道该点的一半是绿色和另一半是红色?那是最坏的情况,对吧?我们绝对不可能猜到一个点的颜色:它是完全随机的!在这种情况下,熵由下面的公式给出(我们有两个类(颜色)–红色或绿色-因此为2):
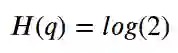
对于介于两者之间的所有其它情况,我们可以用以下公式计算分布的熵,例如q(y),其中_C_是类的数量:
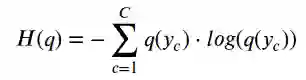
因此,如果我们知道随机变量的真实分布,则可以计算其熵。但是,如果是这样的话,为什么还要训练分类器呢?毕竟,我们知道真正的分布…
但是,如果我们不知道真实分布呢?我们可以尝试用其他一些分布(例如p(y))来近似真实分布吗?我们当然可以!:-)
交叉熵(Cross-Entropy)
假设我们的点遵循这个其它分布p(y) 。但是,我们知道它们实际上来自真(未知)分布q(y) ,对吧?
如果我们这样计算熵,我们实际上是在计算两个分布之间的交叉熵:
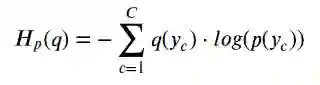
如果我们奇迹般地将p(y)与q(y)完美匹配,则交叉熵和熵的计算值也将匹配。
由于这可能永远不会发生,因此交叉熵将比在真实分布上计算出的熵具有更大的值。
事实上,交叉熵和熵之间的差还有个名字……
KL散度(Kullback-Leibler Divergence)
Kullback-Leibler Divergence,简称“ KL散度 ”,是两个分布之间差异的一种度量:
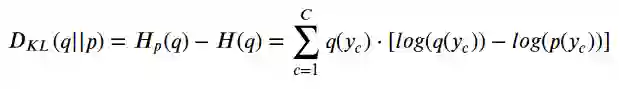
这意味着,p(y)越接近q(y) ,差异越少,因此交叉熵也越小。
因此,我们需要找到一个合适的p(y)……但是,这不就是我们的分类器应该做的吗?确实如此!它寻找可能的最佳p(y),以最小化交叉熵的值。
损失函数
在训练过程中,分类器使用其训练集中的N个点中的每一个来计算交叉熵损失,从而有效地拟合分布p(y)!由于每个点的概率为1 / N,因此交叉熵的计算公式为:

还记得上面的图6至图10吗?我们需要在与每个点的实际类相关的概率上计算交叉熵。这意味着对正类(y = 1)中的点使用绿色条,对负类(y = 0)中的点使用红色的悬挂条,或者从数学角度看:
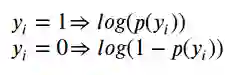
最后一步是计算两个正负类所有点的平均
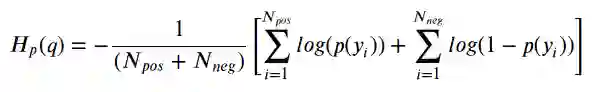
最后,我们通过一点小处理,正类或负类中任何一点都可以用相同的公式:

瞧!我们回到了二进制交叉熵/对数损失的原始公式 :-)
最后
我真的希望这篇文章能够为一个常被认为是理所当然的概念- 二值交叉熵作为损失函数的概念-提供新的思路。此外,我也希望它能向您展示一些机器学习和信息论如何联系在一起的。
来源:https://towardsdatascience.com/understanding-binary-cross-entropy-log-loss-a-visual-explanation-a3ac6025181a
推荐阅读
-
深入理解计算机视觉中的损失函数
-
梯度下降的可视化解释(Adam,AdaGrad,Momentum,RMSProp)
-
最牛损失函数解读:A General and Adaptive Robust Loss Function







