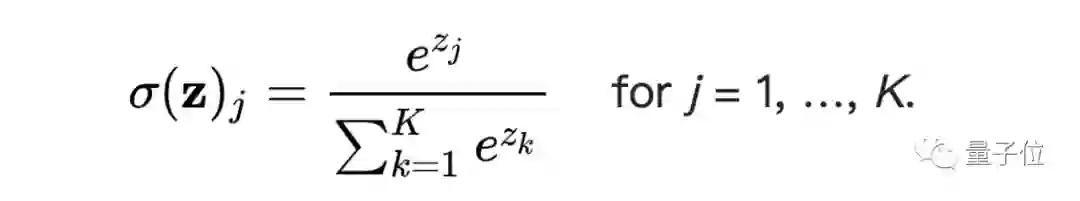谷歌提出新分类损失函数：将噪声对训练结果影响降到最低

晓查 发自 凹非寺 
量子位 报道 | 公众号 QbitAI

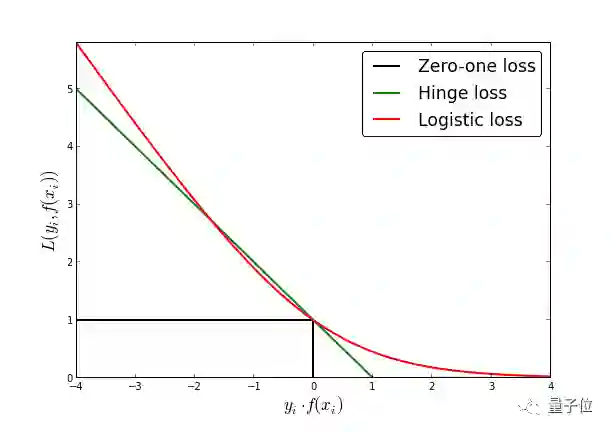
训练数据集里的标签通常不会都是正确的，比如图像分类，如果有人错误地把猫标记成狗，将会对训练结果造成不良的影响。

如何在不改变训练样本的情况下，尽可能降低这类噪声数据对机器学习模型的影响呢？

最近，谷歌提出了一个新的损失函数，解决了机器学习算法受噪声困扰的一大问题。

逻辑损失函数的问题

机器学习模型处理带噪声训练数据的能力，在很大程度上取决于训练过程中使用的损失函数。

通常我们用来训练图像分类的是逻辑损失函数（Logistic loss），但是它存在两大缺点，导致在处理带噪声的数据时存在以下不足：

1、远离的异常值会支配总体的损失

逻辑损失函数对异常值非常敏感。这是因为损失函数的没有上界，而错误的标记数据往往远离决策边界。

这就导致异常大的错误数值会拉伸决策边界，对训练的结果造成不良影响，并且可能会牺牲其他的正确样本。

2、错误的标签的影响会扩展到分类的边界上

神经网络的输出是一个矢量激活值，一般对于分类问题，我们使用的是softmax，将激活值表示为分别属于每个分类的概率。

由于逻辑损失的这种传递函数的尾部以指数方式快速衰减，因此训练过程将倾向于使边界更接近于错误标记的示例，以保证不属于该分类的函数值更接近于0。

如此一来，即使标签噪声水平较低，网络的泛化性能也会立即恶化。

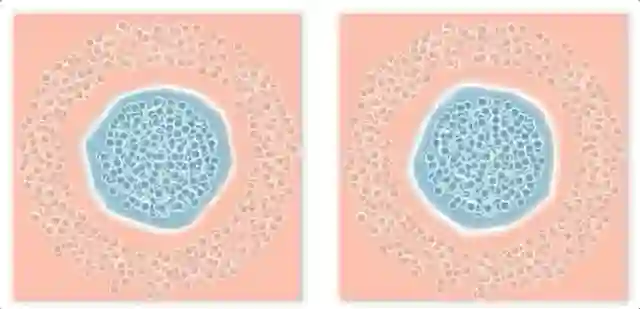
△ 二元分类的可视化结果，噪声会导致决策边界外扩，造成分类错误

双参数可调的损失函数

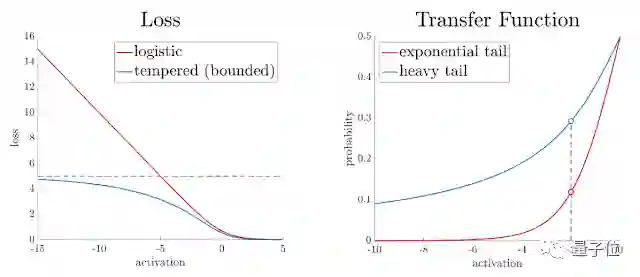
谷歌通过引入两个可调参数的双稳态逻辑损失函数（Bi-Tempered Logistic Loss）来解决上述两个问题。这两个参数分别是“温度”（temperature）t₁和尾部重量（tail-heaviness）t₂。尾部重量其实就是指传递函数尾部下降的速率。

当t₁和t₂都等于1的时候，这个双稳态函数就退化为普通的逻辑损失函数。

温度参数t₁是一个介于0到1之间的参数，它的数值越小，对逻辑损失函数界限的约束就越厉害。

尾部重量t₂定义为一个大于等于1的参数，其数值越大，尾部就越“厚”，相比指数函数来说衰减也就越慢。

△ 温度（左）和尾部重量（右）对损失函数结果的影响

你也可以通过谷歌的在线Demo观察损失函数随t₁和t₂两个参数的变化情况。

对噪声数据集的效果

为了证明不同温度t₁的影响，谷歌在合成数据集上训练一个双层神经网络的二元分类问题。蓝点和红点表示数据实际分属的类别，两个不同颜色的区域表示神经网络的训练结果，白色为决策边界。

谷歌使用标准的逻辑损失函数和不同温度参数的损失函数，对比了在这四种条件下的实验结果：无噪声数据集、小边距噪声数据集、大边距噪声数据集和随机噪声的数据集。

在无噪声情况下，两种损失都能产生良好的决策边界，从而成功地将这两种类别分开。

小边距噪声，即噪声数据接近于决策边界。可以看出，由于softmax尾部快速衰减的原因，逻辑损失会将边界拉伸到更接近噪声点，以补偿它们的低概率。而双稳态损失函数有较重的尾部，保持边界远离噪声样本。

大边距噪声，即噪声数据远离决策边界。由于双稳态损失函数的有界性，可以防止这些远离边界的噪声点将决策边界拉开。

最后一个实验是随机噪声，噪声点随机分布在矢量空间中。逻辑损失受到噪声样本的高度干扰，无法收敛到一个良好的决策边界。而双稳态损失可以收敛到与无噪声情况几乎相同的结果上。

传送门

在线Demo：
https://google.github.io/bi-tempered-loss/

博客地址：
https://ai.googleblog.com/2019/08/bi-tempered-logistic-loss-for-training.html

论文链接：
https://arxiv.org/abs/1906.03361

— 完 —

加入社群 | 与优秀的人交流

小程序 | 全类别AI学习教程

量子位 QbitAI · 头条号签约作者

վ'ᴗ' ի 追踪AI技术和产品新动态

喜欢就点「好看」吧 ！