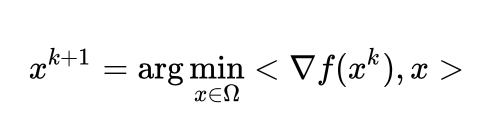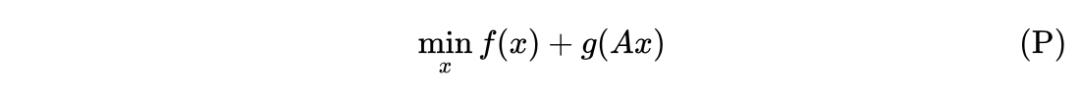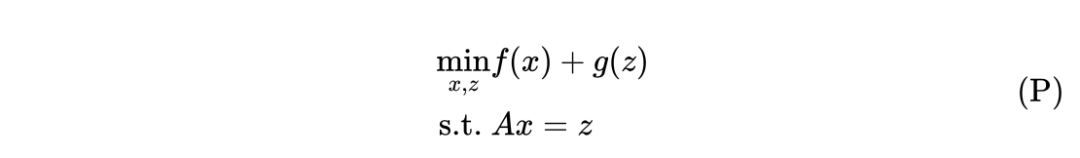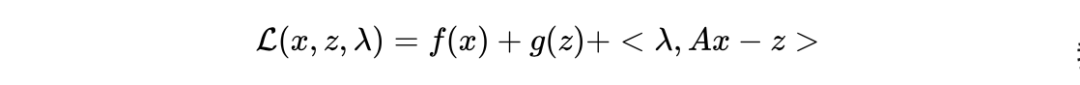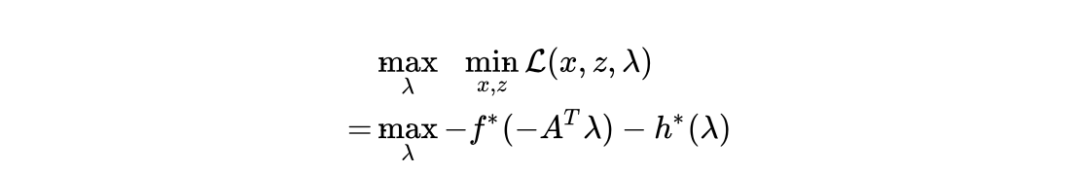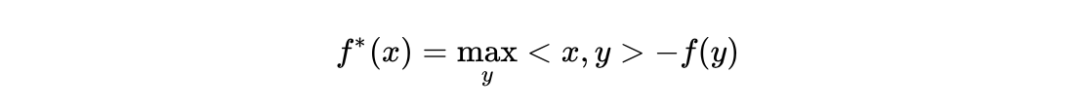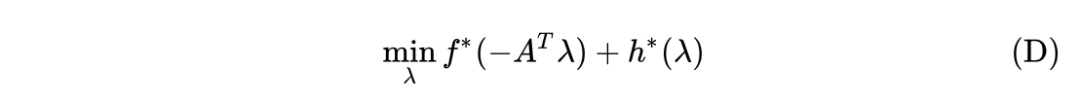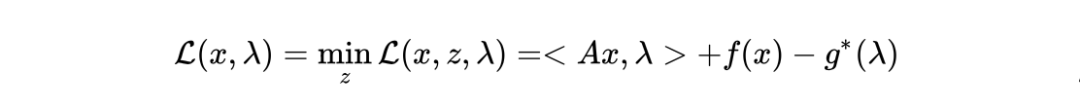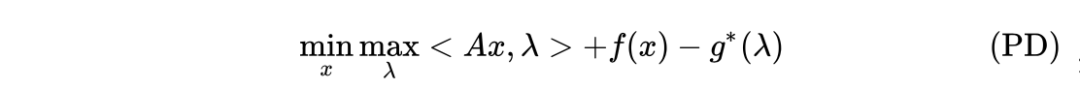加入极市专业CV交流群,与6000+来自腾讯,华为,百度,北大,清华,中科院等名企名校视觉开发者互动交流!更有机会与李开复老师等大牛群内互动!
同时提供每月大咖直播分享、真实项目需求对接、干货资讯汇总,行业技术交流。关注 极市平台 公众号 ,回复 加群,立刻申请入群~
作者:邓康康
链接:https://zhuanlan.zhihu.com/p/85423364
本文已由作者授权转载,未经允许,不得二次转载
这篇文章想讲述下我接触到的优化方法,从确定到随机,从一阶到二阶,从原始到对偶,
光滑到非光滑。
我认为迭代算法就是不断逼近,化繁为简,将一个个难问题分为若干个易问题的过程。
所以我从逼近的角度去讲述这些方法。
欢迎大家来讨论交流,由于能力有限,难免有疏漏或错误之处,望指正。
一、Deterministic Methods
首先最早的是梯度方法,假设我们有一个迭代点
![]() ,梯度方法通过在该点做一个泰勒展开得到一个局部逼近的二次函数,然后求解该二次函数得到
,梯度方法通过在该点做一个泰勒展开得到一个局部逼近的二次函数,然后求解该二次函数得到
![]() 这里的
这里的
![]() 为步长,步长的选择有很多种,比如最速下降法这样选择步长
或者采用线搜索的形式找到一个满足线搜索的步长即可。
更快速的步长为一种叫BB方法的步长
为步长,步长的选择有很多种,比如最速下降法这样选择步长
或者采用线搜索的形式找到一个满足线搜索的步长即可。
更快速的步长为一种叫BB方法的步长
这个步长其实是对Hessian矩阵的一个近似,可以叫它伪二阶方法。
BB步长及其有效,对于某些方法的提速有奇效,你可以在各种新的方法中看到它的身影。
可惜不是单调的,对于一般非线性函数没有收敛性保障,所以通常会结合线搜索使用。
最后说一下共轭梯度方法,这个方法可以这样理解: 它觉得负梯度方向不好,所以去改良它,用上一步方向对它做一个矫正。
共轭梯度方法其实动量方法还有heavy ball方法非常相似,感兴趣的可以去了解下。
如果我们对原函数做二阶泰勒展开,那么将得到二阶算法
这就是牛顿方法。
当维数太大时,求解Hessian矩阵的逆很费时间,所以我们就去用向量逼近,这样就得到了拟牛顿方法,这里就不讲了。
有时候我们希望能够控制每一步走的幅度,根据泰勒展开的逼近程度来决定我们这一步要走多远,这样就得到了信赖域方法
这里的
![]() 为信赖域半径,如果泰勒展开逼近的好,我们就扩大半径,否则就缩小半径。
为信赖域半径,如果泰勒展开逼近的好,我们就扩大半径,否则就缩小半径。
为什么没有更高阶的算法呢?
个人觉得二阶已经够难的了,高阶在计算上是行不通的。
当然,也许对于某些特定问题高阶是可行的。
二、Stochastic Methods
第一节中提到的方法迭代过程本身就是对问题的一种逼近,每一次迭代,最低的代价也要算一次梯度。
对于问题(2),如果n很大的时候,算一次完整的函数梯度都费劲,这时候就可以考虑算部分函数梯度。
当n太大的时候,计算梯度太耗时了,所以SGD只用部分的梯度去得到一个逼近函数,每次随机选择一个梯度:
一个变种是minibatch size,也就是一次选择若干个。
2. 方差削减类随机方法(variance reduction)
目前所有的随机方法似乎都是在随机和方差削减之间做权衡,SGD每次选一个,这样太随机,导致方差过大。
梯度方法每次选所有,这样方差为0,但是不随机啊,这样当n太大的时候,他就太慢了。
所以就衍生出了很多的随机变种方法,比如批量梯度(每次选多个),SVRG,SARAH等等。
这里要讲起来就太多太多了。
自己去看吧。
一阶方法的缺陷就是精度不够高,所以有时候还是需要用到二阶方法,但是呢,我们又嫌二阶方法太慢,所以干脆就对Hessian矩阵也采样,这样就得到了subsample Newton方法
当然类似的信赖域以及cubic正则方法也有对应的随机变种出现了。
三、临近类方法
临近类方法是用于处理目标函数中含有非光滑项,并且该非光滑项是“临近友好的”,意思就是它的临近算子是容易计算的,或是有闭式解。
首先考虑一般问题
这里的f是光滑的,而g为非光滑的,通常为某种正则函数,一范数之类的,当然也有可能为某个约束集的指示函数,这个时候就变成约束优化问题了。
首先定义g的临近算子
![]() 当
当
![]() ,PPA有如下迭代
其实就是梯度方法的一个扩展,同样也是把光滑项做泰勒展开,非光滑项就不管它
注意到如果g恒等于0,那么临近梯度算法就是梯度方法,如果f恒等于0,那么就变成了PPA。
如果
,PPA有如下迭代
其实就是梯度方法的一个扩展,同样也是把光滑项做泰勒展开,非光滑项就不管它
注意到如果g恒等于0,那么临近梯度算法就是梯度方法,如果f恒等于0,那么就变成了PPA。
如果
![]() ,那么PGA就变成了投影梯度方法了(神奇吧)。
Remark:
需要注意的是,这个算法的主要在于求解临近算子,所以一定要“临近友好”才行。
另外这个算法还有很多变种,比如著名的FISTA,本质上就是PGA结合了Nestov加速策略。
和前面几类方法的扩展如出一辙,既然可以做一阶泰勒展开,当然也可以做二阶,于是。
。
当n比较大的时候,我们每次只对其中一个或者多个fi做泰勒展开
同样的,当g恒等于0时,这不就是随机梯度吗,那么可能大家自然会想到,既然随机梯度可以平行过来,那其他的随机类方法呢?
是的,都有了,所有的随机类方法都已经平行过来了(我们能想到的,别人也想到了,哎!
)当然也有些随机临近牛顿法等等。
Remark:
如果从算子分裂的角度看临近类方法,我们可以知道梯度方法为forward iteration(向前),临近点为backward iteration(向后),那么临近梯度则为forward-backward iteration,可以这样理解,PGA就是先走个梯度步,然后再走个临近步。
从这个角度出发,我们又可以延伸出很多方法,比如Peaceman-Rachford 以及 Douglas-Rachford,这个我会在另外一篇文章中详细讲讲(还没写。
。
)
这个方法最早是求解约束优化问题,后面延伸到以下一般问题
上面的子问题就是非光滑项加一个线性项,当
,那么PGA就变成了投影梯度方法了(神奇吧)。
Remark:
需要注意的是,这个算法的主要在于求解临近算子,所以一定要“临近友好”才行。
另外这个算法还有很多变种,比如著名的FISTA,本质上就是PGA结合了Nestov加速策略。
和前面几类方法的扩展如出一辙,既然可以做一阶泰勒展开,当然也可以做二阶,于是。
。
当n比较大的时候,我们每次只对其中一个或者多个fi做泰勒展开
同样的,当g恒等于0时,这不就是随机梯度吗,那么可能大家自然会想到,既然随机梯度可以平行过来,那其他的随机类方法呢?
是的,都有了,所有的随机类方法都已经平行过来了(我们能想到的,别人也想到了,哎!
)当然也有些随机临近牛顿法等等。
Remark:
如果从算子分裂的角度看临近类方法,我们可以知道梯度方法为forward iteration(向前),临近点为backward iteration(向后),那么临近梯度则为forward-backward iteration,可以这样理解,PGA就是先走个梯度步,然后再走个临近步。
从这个角度出发,我们又可以延伸出很多方法,比如Peaceman-Rachford 以及 Douglas-Rachford,这个我会在另外一篇文章中详细讲讲(还没写。
。
)
这个方法最早是求解约束优化问题,后面延伸到以下一般问题
上面的子问题就是非光滑项加一个线性项,当
![]() ,上述问题变为
这就是最开始的条件梯度法,这个方法最初的想法是用于解决那些非“临近友好”的问题,也就是投影不好做的那种问题。
比如如果约束集为单纯型约束时,用这个方法会比投影梯度(也就是临近梯度)好一点。
,上述问题变为
这就是最开始的条件梯度法,这个方法最初的想法是用于解决那些非“临近友好”的问题,也就是投影不好做的那种问题。
比如如果约束集为单纯型约束时,用这个方法会比投影梯度(也就是临近梯度)好一点。
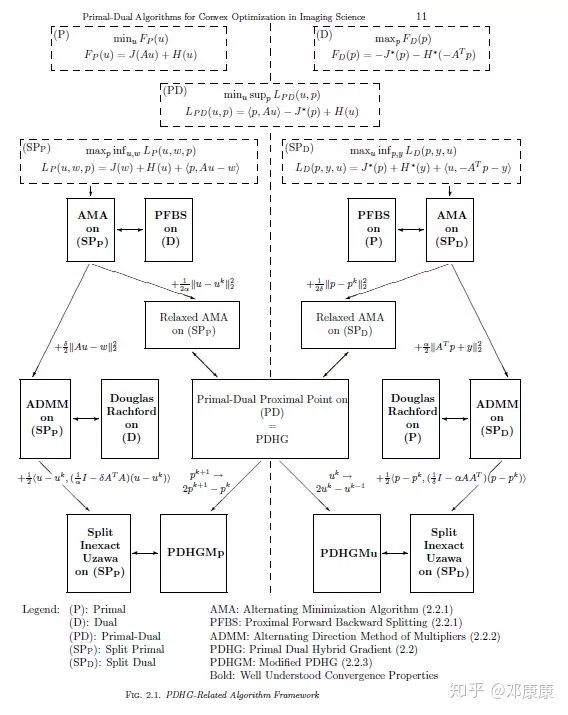
四、对偶类方法
对于一个优化问题,通常可以从三个角度入手设计算法,原始,对偶,原始对偶(也就是鞍点问题)。
我们首先引入一个例子来得到这三个问题。
考虑一般问题
这就是原始问题,从原始角度出发的话,我们可以对该问题构造增广拉格朗日方法ALM,交替方向乘子法ADMM等。
接下来讨论对偶角度,首先得到拉格朗日函数
另外还有一种就是原始对偶表达,我们只需要对拉格朗日函数关于z求极小,得到的目标就是原始对偶问题,也叫做鞍点问题
从“approximations”角度看,很多优化方法都离不开一个工具:
泰勒展开
。
CV细分方向交流群
添加极市小助手微信(ID : cv-mart),备注:研究方向-姓名-学校/公司-城市(如:目标检测-小极-北大-深圳),即可申请加入目标检测、目标跟踪、人脸、工业检测、医学影像、三维&SLAM、图像分割、OCR、姿态估计等极市技术交流群(已经添加小助手的好友直接私信),更有每月大咖直播分享、真实项目需求对接、干货资讯汇总,行业技术交流,一起来让思想之光照的更远吧~
![]()
△长按添加极市小助手
![]()
△长按关注极市平台
觉得有用麻烦给个在看啦~ ![]()
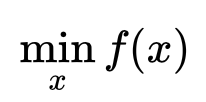
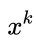 ,梯度方法通过在该点做一个泰勒展开得到一个局部逼近的二次函数,然后求解该二次函数得到
,梯度方法通过在该点做一个泰勒展开得到一个局部逼近的二次函数,然后求解该二次函数得到
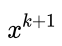
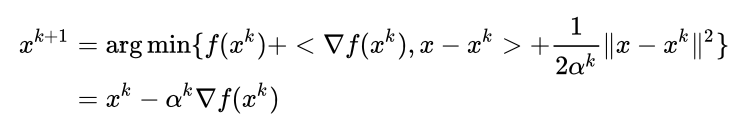
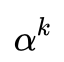 为步长,步长的选择有很多种,比如最速下降法这样选择步长
为步长,步长的选择有很多种,比如最速下降法这样选择步长
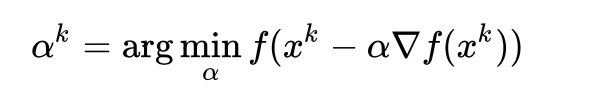
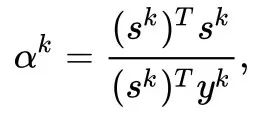
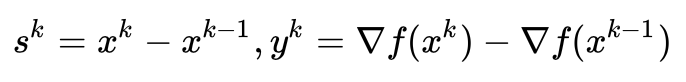
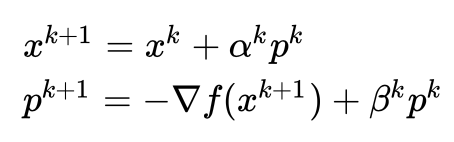
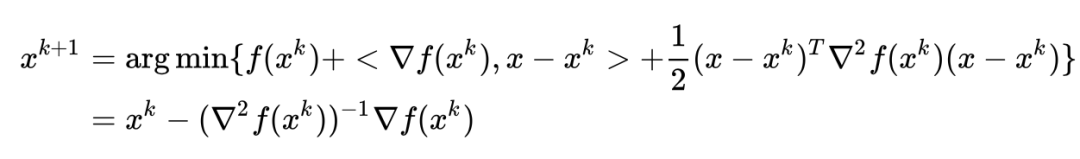
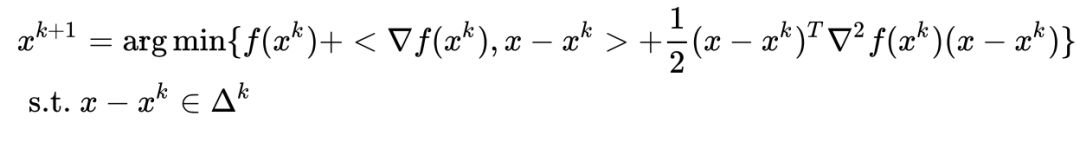
 为信赖域半径,如果泰勒展开逼近的好,我们就扩大半径,否则就缩小半径。
为信赖域半径,如果泰勒展开逼近的好,我们就扩大半径,否则就缩小半径。
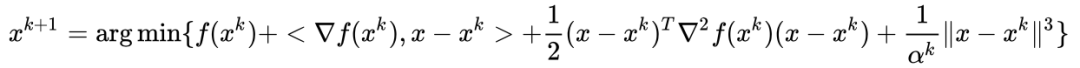
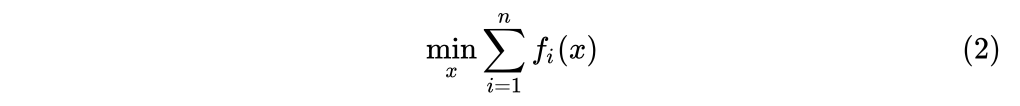
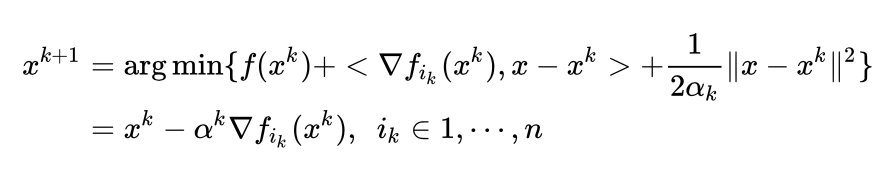
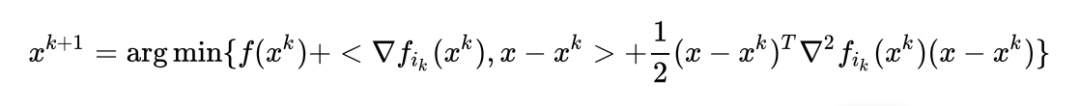
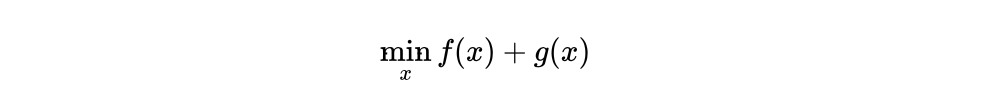
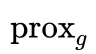
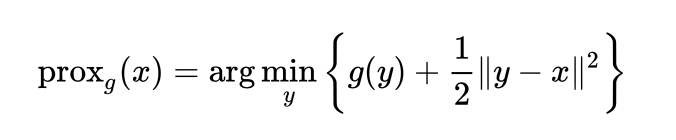
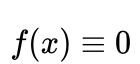 ,PPA有如下迭代
,PPA有如下迭代
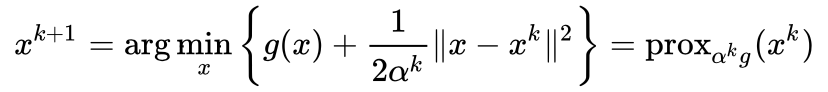
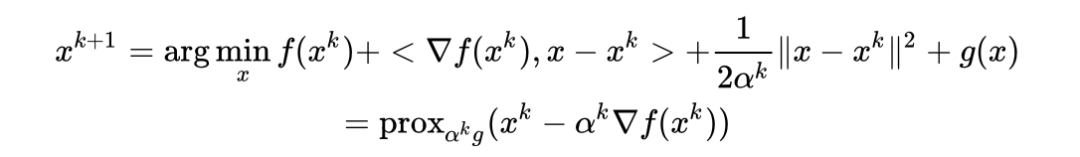
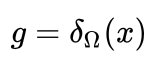 ,那么PGA就变成了投影梯度方法了(神奇吧)。
,那么PGA就变成了投影梯度方法了(神奇吧)。
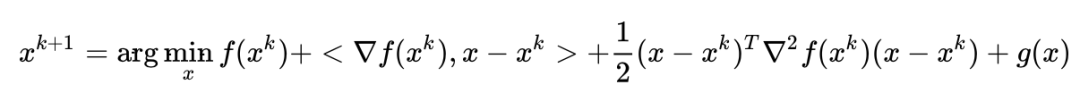
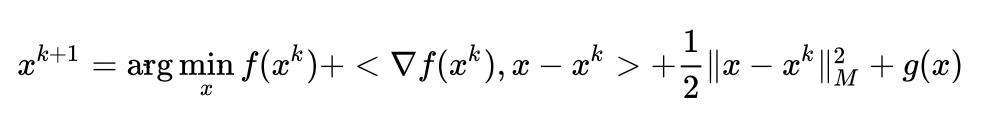
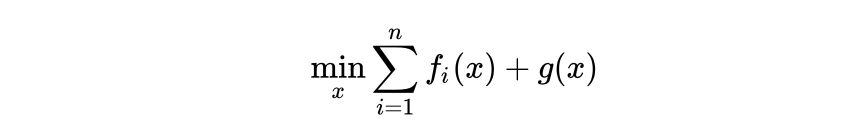
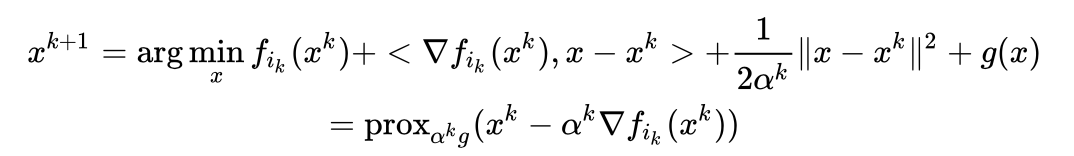
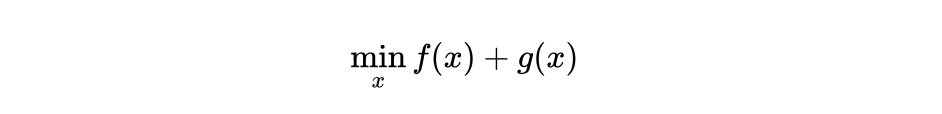
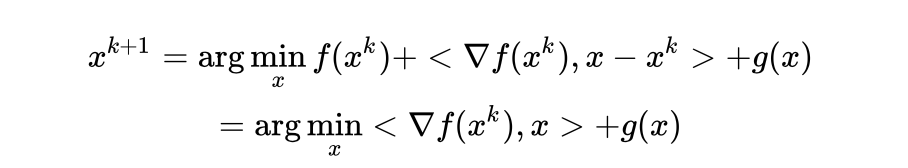
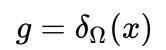 ,上述问题变为
,上述问题变为