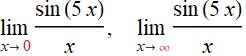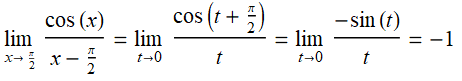【三角函数的极限和导数】图解普林斯顿微积分06

第7 章 三角函数的极限和导数

本章主要内容:

• 三角函数在小数、大数以及其他变量值时的行为;

• 三角函数的导数;

• 简谐运动.

7.1 三角函数的极限

考虑下面两个极限, 唯一区别是, 左边极限考察的是在 x 趋于 0 , 而右边在 x 趋于无穷大取的极限. 也就是需要留意是在很小很小数, 还是很大很大的数上取得极限.

7.1.1 小数的情况

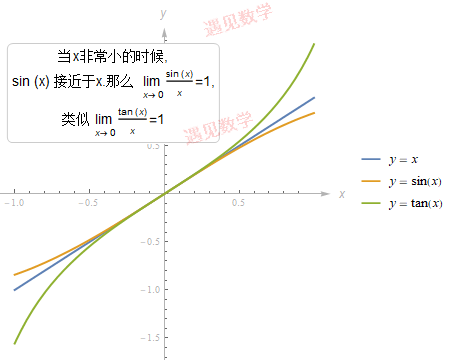
事实表明, sin(x) 和 x 在 0 附近近似相等, 观察下面 x 在 -1 和 1直接的图形, 当 x 非常非常小的时候, sin(x) 近似等于 x , 那么 $\frac{\sin \left(x\right)}{x}\text{=1}$成立.

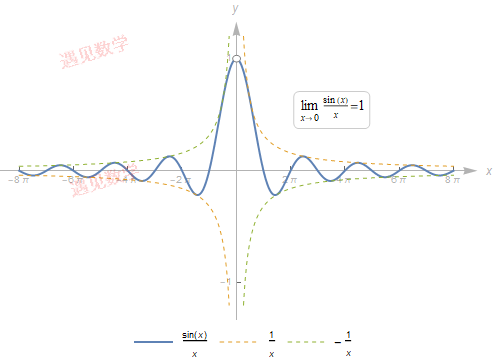
7.1.3 大数的情况

7.1.4 "其他的"情况

如果计算 x 趋于 a 的极限, 这里 $a\ne 0$ , 这里有一个解决的方法, 就是用 $\text{t=x-a}$ 做替换, 将问题转化为 t 趋近于 0 , 比如下面的例子:

7.1.5 一个重要极限的证明

7.2 三角函数的导数

现在把所有三角函数以及反三角函数做个总结(公式自: 中文维基百科).

反三角函数的导数:

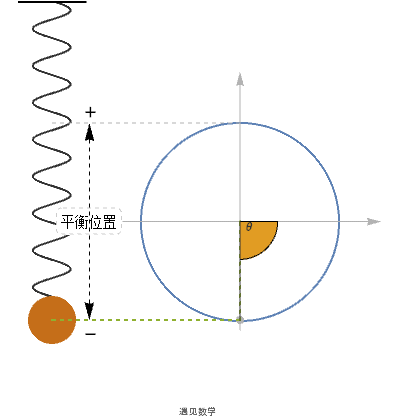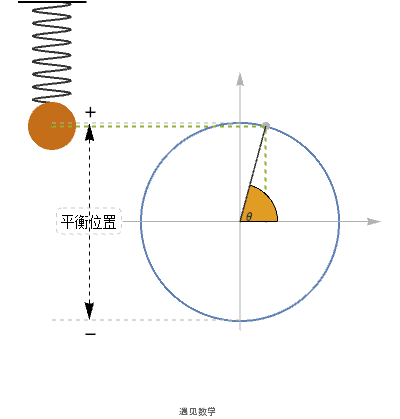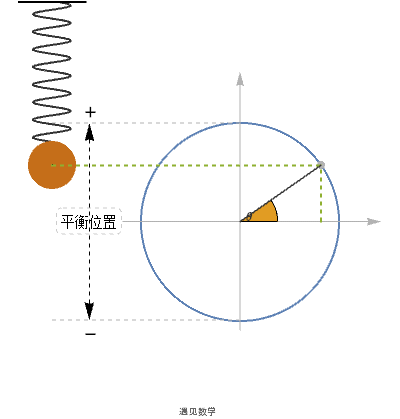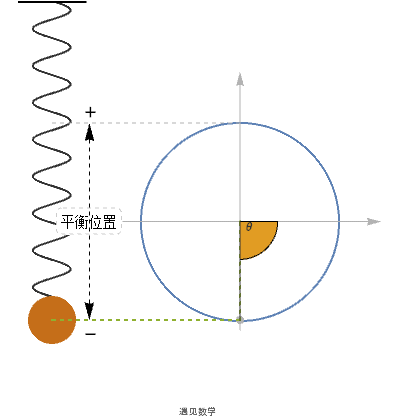
7.2.2 简谐运动(Simple harmonic motion)

三角函数经常会用来描述弹簧的震荡运动. 设 x 是弹簧振子在时刻 t 的位置, 取向上的方向作为正方向, 那么描述 x 的方程大致类似于x = r sin (ω t). 类似也可以用余弦来代替, 因为两者总是来回震荡, 而这类运动就被称为简谐运动.

(本章完)

「予人玫瑰, 手留余香」

您能帮助[遇见数学]更快发展吗?感谢支持!