TKDE'22 图表示学习汇总一个非常好用的trick

论文题目：Learning Regularized Noise Contrastive Estimation for Robust Network Embedding
文章链接：https://shawxh.github.io/assets/rnce.pdf
代码链接：https://github.com/ShawXh/RNCE

网络节点嵌入（network embedding）中许多方法基于噪声对比估计（noise constrative learning, NCE）。这类方法以自然语言处理中的word2vec为基础，包括了node2vec[1]，deepwalk[2]等经典算法，在学术界和工业界都获得了非常广泛的应用。这些方法的主要区别在于对于节点邻域的选择上（通过随机游走等方法）。本文总结了两种典型的NCE-based的网络嵌入方法的目标函数，从多个角度进行了理论的分析，最后提出通过在目标函数中添加一个距离项来规范学习的过程，使得得到的节点嵌入表示结果更加鲁棒。

本文提到的方法及相关结论在计算机视觉中对比学习领域最近的文章里也有提及。例如，ICML'20[3]中提出的alignment loss，实际上是本文提出的regularized distance function的一个特殊版本（高斯），以及 ICLR'22[4]中提到的dimensional collapse[5] 和本文提到的基于NCE的网络嵌入的扁平化的节点表示也异曲同工。

另外，本文提到的方法在网络节点嵌入领域在TKDE'20[6]、KDD'21[7] 中已经被采用，在开源图计算库DGL中也已被集成（LINE[8]，DeepWalk[9]）。

1 背景

节点嵌入： 给定网络 ，其中 是节点集合， 是边的集合， 是有向边 的权重，我们假定有向边为正边，即 。在实际应用过程中， 通常由算法设计者根据特定场景进行设计（例如当特别关注某种类型的节点亲密度）。

基于NCE的节点嵌入： 与图神经网络等常用于处理带属性网络的方法相比，基于NCE的网络节点嵌入通常用于对网络的拓扑信息进行表示嵌入。同时，基于NCE的方法常常有更好的可扩展性，可以在单机上实现对百万级节点网络的嵌入表示，也常作为提供预训练的表示向量的一种方式为下游任务服务。

对于每一对 的节点对 ，基于NCE的方法有两种形式的目标函数，记为 ，数学表达式如下：

其中， 是节点 的表征向量（node embedding）， 是节点 的隐藏向量（hidden embedding）， 是一个（常常被预先定义好的）负样本的分布。 可以看到， 和 的主要区别在于是否使用了隐藏向量。不失一般性地，本文主要从 出发开展讨论，得到的结论也可以很容易地扩展到 。 NCE之所以叫噪声对比估计，因为目标函数 中包含了一项对正样本的score function和一项对于负样本的噪声建模，这也是对比学习（contrastive learning）的一个基本思路。

基于 ，最终的目标函数被定义为：

2 基于Regularized NCE（RNCE）的网络嵌入

先说结论，只想知道trick的朋友到此可以结束阅读了。在原始目标函数 中加入一个距离项 就可以使得NCE在诸多方面的性质获得改进：

需要满足：

其中 是一个与距离函数相关的系数（常量或变量）。满足这种性质的距离函数有很多，包括但不限于：

• Elastic energy function 弹性势能函数（ 是劲度系数）

• Wasserstein- 距离 Wasserstein- 距离被定义为 ，为了便于计算，取 次方，可以得到

• Gaussian核函数

• Laplacian核函数

Wasserstein-3 距离最理想。 具体分析可以参考原文。

3 理论分析

文中涉及到较多的理论推导，这里只给出结论，感兴趣的读者可以阅读原文。

Q1: 基于NCE的网络嵌入到底在做什么？

A1: 对每一对正样本 , 考虑向量 和 。记第 步的节点嵌入为 和 ，通过以下结论，基本可以看出基于NCE的网络嵌入在做什么：

1. 向量内积 趋于正无穷（[10]也曾提到，但只给了理论解，并没有证明这个理论解是否可以达到），即：

2. 向量内积 收敛到正无穷的速率为（ 为学习率）：

3. 向量 和 会无限接近，即：

4. 的收敛速率：

5. 向量 和 的方向会收敛到同一个位置，即：

Q2: RNCE能多大程度加速模型的收敛？会不会改变模型最终的收敛点？

A2: 与 A1 中的第4点相比，RNCE的收敛速率为：

当 较大时，我们有 , 与 NCE 相比， 。所以 RNCE 的收敛速率大约是 NCE 的 倍. 同时，易证， RNCE 并不会改变 NCE 的收敛点（A1 中的1、3、5点）。

Q3: NCE 和 RNCE 在保留一阶亲密度（邻接节点间的亲密度）的理论性能对比？

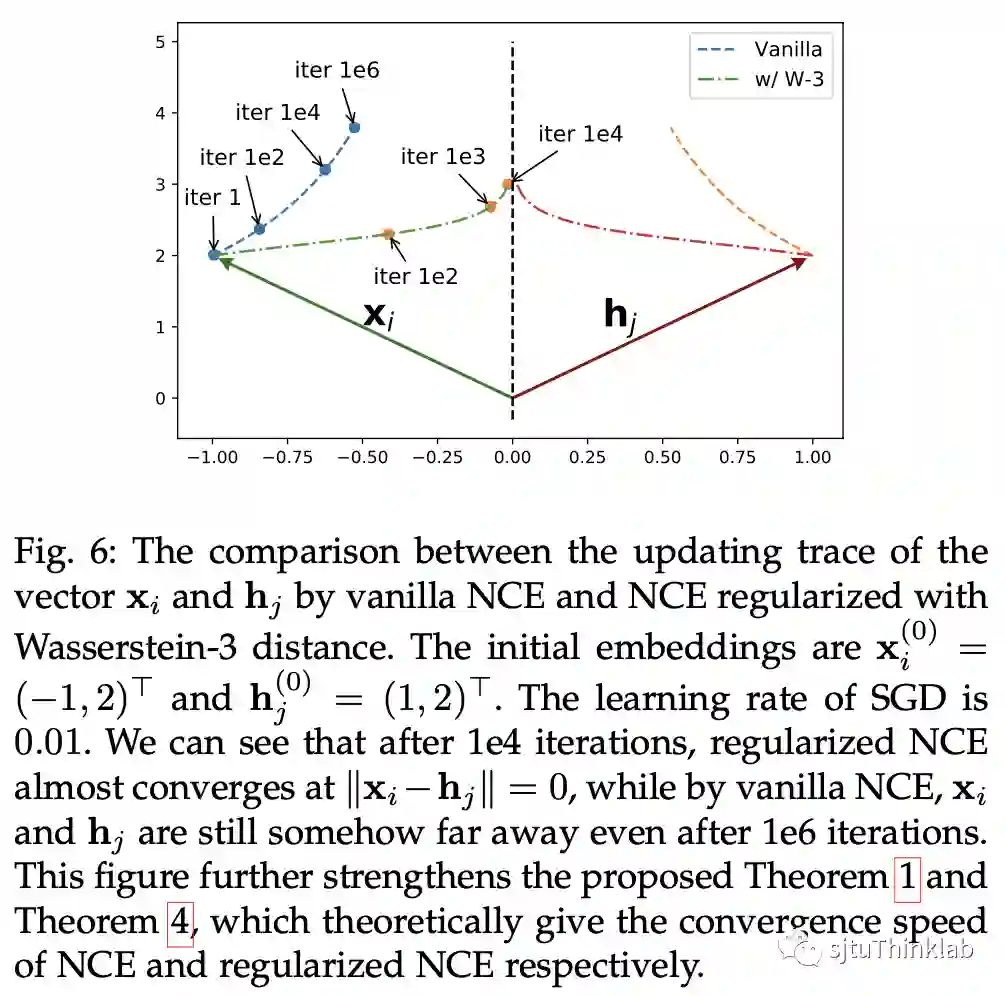
A3: NCE 的理论性能不理想。 A1 中第三点提到向量 和 会无限接近，说明了当优化时的迭代次数趋于无穷，一阶相似度（即 和 的相似度）可以被很好的保留，然而现实中机器学习的过程中迭代次数相当有限。通过求导可以得到 ，当 比较大的时候，梯度会处于一个接近消失的状态，造成了训练中后期模型收敛速率变得十分缓慢，也就是在有限步内，模型很难达到 的收敛状态。

下图比较清楚地展示了这个问题，虚线是基于NCE的embedding，点划线是基于RNCE的embedding，经过1,000,000轮迭代，NCE模型依然距离收敛有着较大的距离，而经过1,000轮迭代，（在合理的参数下的）RNCE已经非常接近收敛极限。

加入的距离函数 保证了 RNCE 对于一阶亲密度的保留性能。

Q4: NCE和RNCE在保留二阶亲密度（拥有共同邻居的节点间的亲密度）的理论性能？

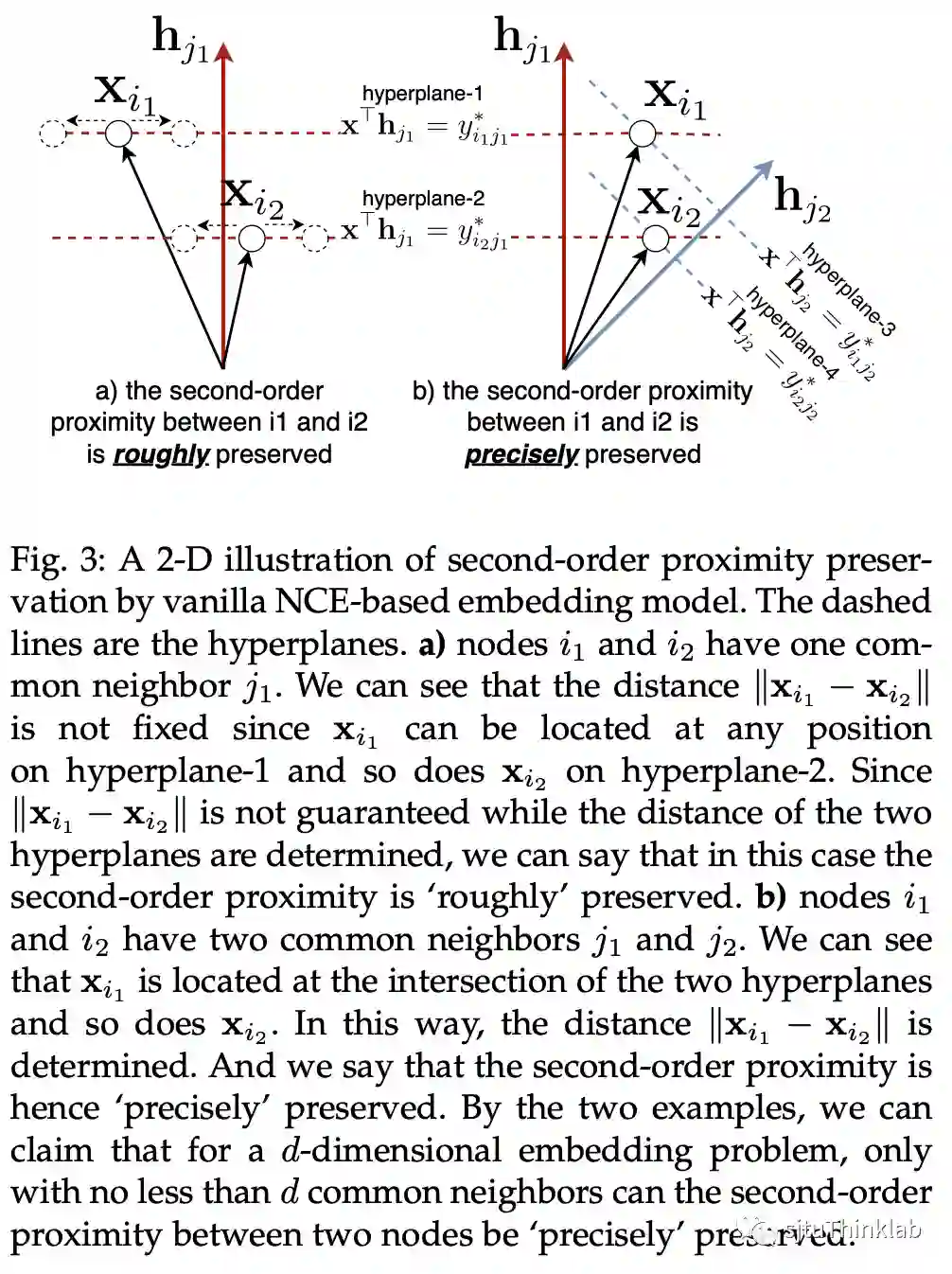
A4: 只有当两个节点间的共同邻居数量大于等于向量的维度时，二阶亲密度才能被较好地保留。 下面这张图比较清晰地说明了这一点：

RNCE 对于一阶亲密度的保留性能，保证了其对二阶亲密度的保留性能。

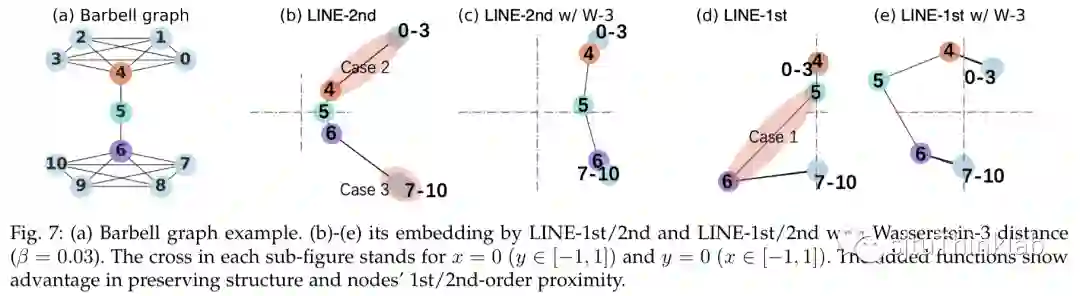
关于 NCE 和 RNCE 对一阶/二阶亲密度的保留性能对比，下图给了一个可视化实例：

Q5: 保留亲密度对模型下游任务有什么好处？

A5: 对于亲密度的保留能力，一方面等同于模型保留原始网络拓扑信息的能力，另一方面，在节点分类任务上，对亲密度对保留相当于在亲密的节点之间做了标签平滑化（label smoothing）。

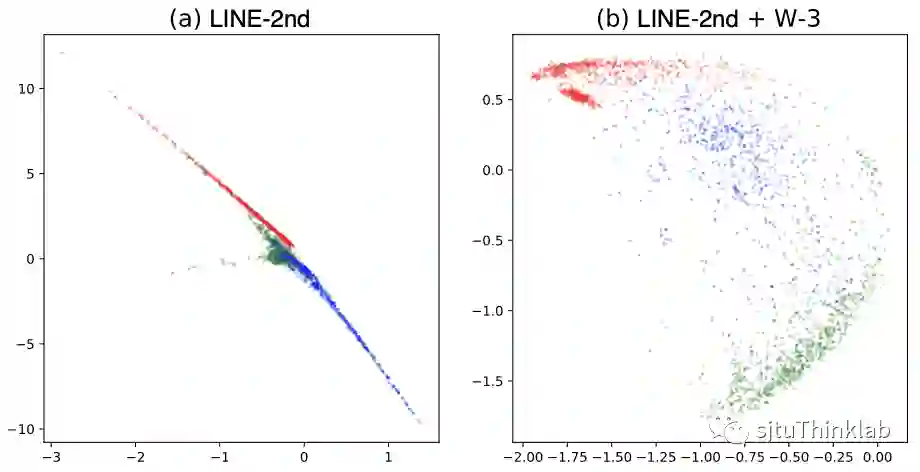
Q6: 造成的扁平化节点表示是怎么回事？

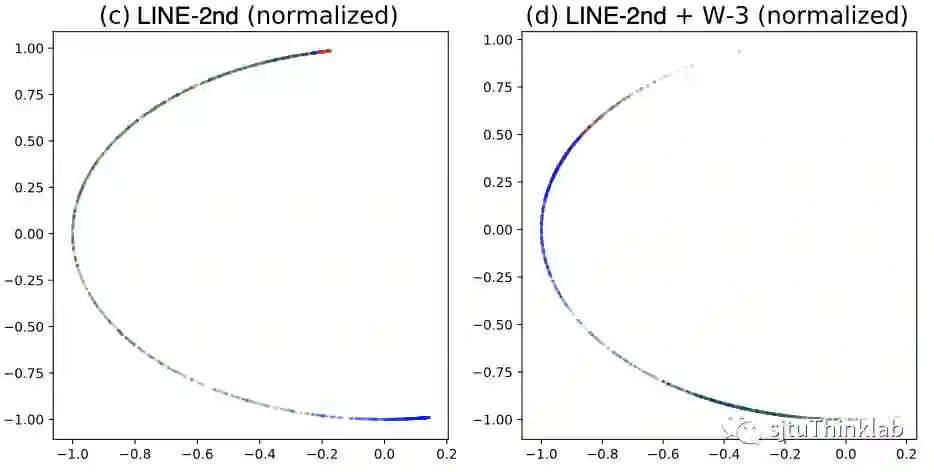
A6: 先看实例，在下图我们对无监督生成的embedding做一个可视化，左边是基于NCE的方法，右边是基于RNCE的方法，不同颜色的点代表了不同类别。可以很清楚地看到，基于NCE得到的embedding大约分布在3条直线，这3条直线交汇于原点，原点附近不同类别的节点分布十分混乱。从某种意义上来看，模型只学会了大约3种embedding。这种高度线性的扁平化的embedding分布，相当于过滤掉了网络中的大部分非常重要的非线性量。 即使经过归一化处理，不同类别之间重合度也非常高。RNCE则很好地区分开了不同类别的节点，也不存在扁平化的embedding分布问题。

实际上，扁平化问题不仅仅发生于同类别的（或者亲密的）节点之间，甚至可以发生在毫无关联的节点之间。 我们通过随机图模型（random graph）论证了这一点：对于一个包含了 个节点、边的生成概率为 的随机图，对其进行网络嵌入后，我们假设模型已经收敛到一个比较好的状态，即，对于任意 的节点对 ，已经有 ， 。那么我们对于任意一个节点 ，我们总能找到这样一个节点 ，使得 的 embedding 几乎与 平行，即 与 和 相比是一个非常小的值。我们记满足这个条件的节点 的数量期望为 ，我们有：

其中 是组合数。

与NCE相比，RNCE不存在扁平化的节点嵌入问题。

4 实验

实验中选取了几个典型的基于NCE的网络嵌入方法作为baseline，与基于RNCE的版本进行了对比。

4.1 节点分类

在数据集YouTube，PPI，BlogCatalog上进行了无监督节点分类的实验，实验结果显示，基于RNCE的方法，可以在不对节点间亲密度进行特征工程方面的设计的情况下，在相同setting下，轻易地超过同类方法的sota，同时只增加了十分微小的计算开销。

BlogCatalog上的对比实验

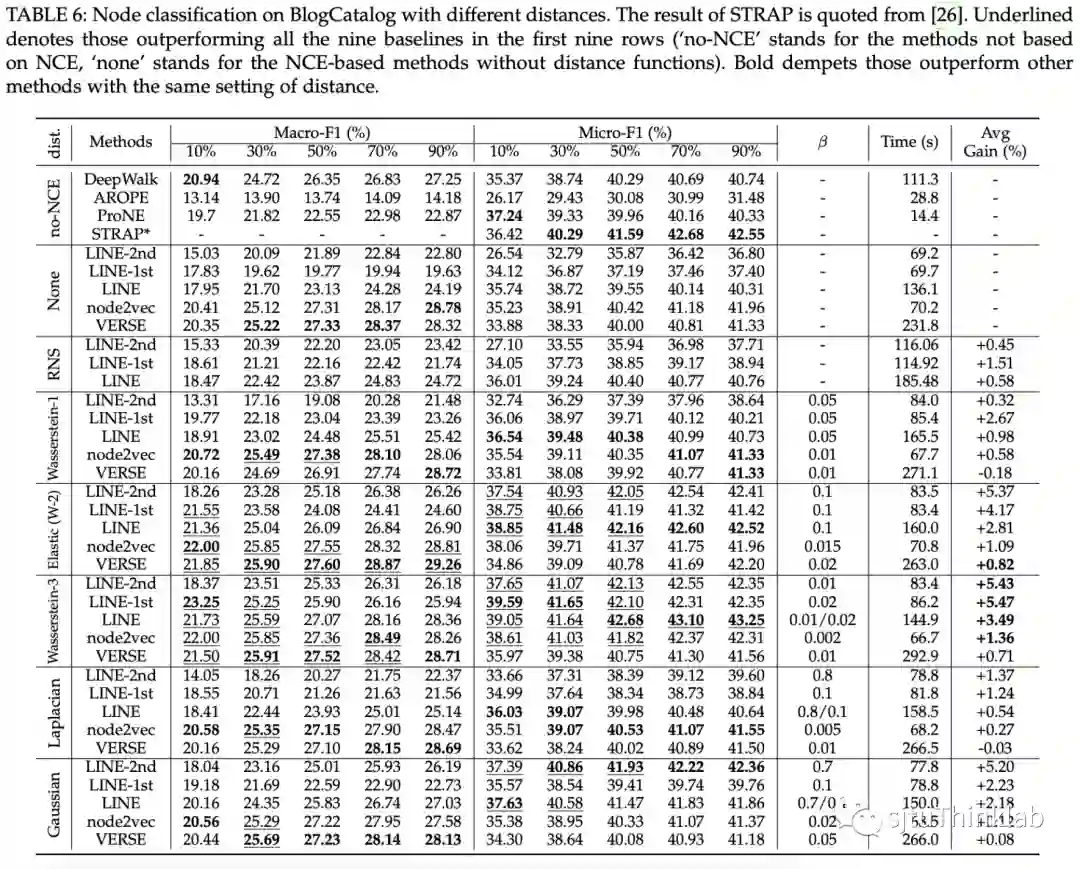
更多实验结果参考原文。

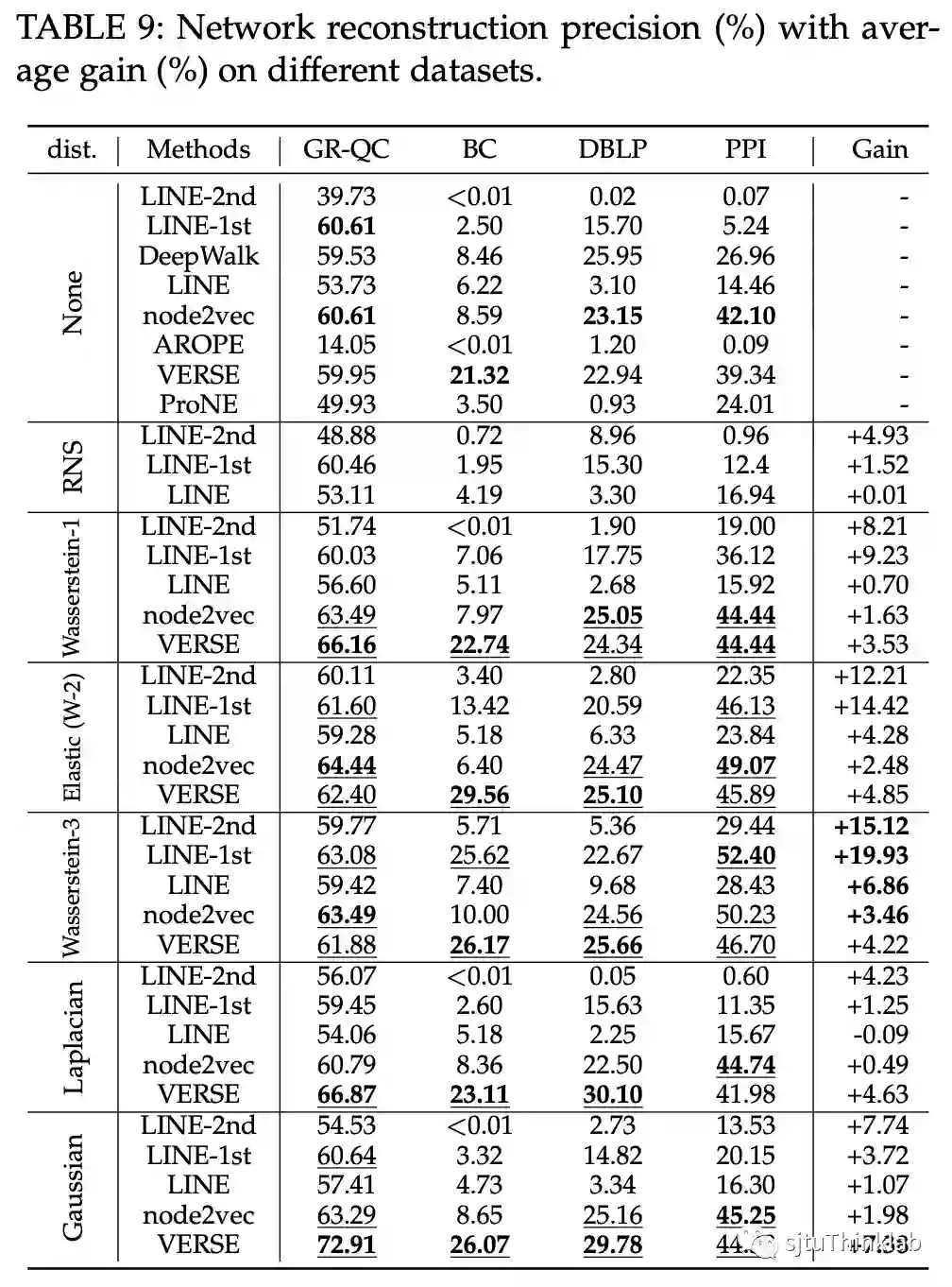
4.2 网络重建

在GR-QC、BlogCatalog、DBLP、PPI上进行了实验。Wasserstein-3 距离可以使LINE保留原始网络结构信息的能力提高十几个百分点。

参考文献

[1]: Grover A, Leskovec J. node2vec: Scalable feature learning for networks. SIGKDD 2016.
[2]: Perozzi B, Al-Rfou R, Skiena S. Deepwalk: Online learning of social representations. SIGKDD 2014.
[3]: Wang T, Isola P. Understanding contrastive representation learning through alignment and uniformity on the hypersphere. ICML 2020.
[4]: Jing L, Vincent P, LeCun Y, et al. Understanding dimensional collapse in contrastive self-supervised learning. ICLR 2022.
[5]: "dimensional collapse": the embedding vectors occupy a lower-dimensional subspace than their dimension
[6]: Xiong H, Yan J. BTWalk: branching tree random walk for multi-order structured network embedding. TKDE 2020.
[7]: Xiong H, Yan J, Pan L. Contrastive Multi-View Multiplex Network Embedding with Applications to Robust Network Alignment. SIGKDD 2021.
[8]: https://github.com/dmlc/dgl/tree/master/examples/pytorch/ogb/line
[9]: https://github.com/dmlc/dgl/blob/master/examples/pytorch/ogb/deepwalk
[10]: Armandpour M, Ding P, Huang J, et al. Robust negative sampling for network embedding, AAAI 2019.