这10个『数学问题』你能答上来，我就送……

免费送课！

就知道你的好胜心态叒叕作祟了

今天小七挑选了10道数学题，“留言框”写下你认为正确的答案，最先全部答对的两位同学（按后台显示时间），将会免费赢取七月在线最新课程《机器学习中的数学第二期》（课程介绍见文末）

下列10道题均选自【七月在线AI题库】数学部分，刷题和查看解析的同学，可点击文末“阅读原文”进入题库（或下载“七月在线”APP)

1. 一家人有两个小孩，其中有一个是女孩，那么另外一个也是女孩的概率（ ）

A. 1/2 

B. 1/3

C. 1/4

D. 2/3

2. 某旅馆内住着不同职业、不同国籍的A，B，C，D四个人，他们来自英、法、德、美四个国家，现已知德国人是医生，美国人年龄最小且是警察、C比德国人年纪大、B是法官且是英国人的朋友，D从未学过医。由此可知C是（ ）

A. 美国人

B. 法国人 

C. 英国人

D. 不确定

3. 有A、B、C、D四个人，要在夜里过一座桥。他们通过这座桥分别需要耗时1、2、5、10分钟，只有一支手电筒，并且同时最多只能两个人一起过桥。请问，最短需要（ ）分钟四人都能过桥？

A. 17

B. 19

C. 21

D. 15

4. 一面墙，单独工作时，A花18小时砌好，B花24小时，C花30小时，现A,B,C的顺序轮流砌，每人工作1小时换班，完工时，B总共干了多少小时？（ ）

A. 8小时

B. 7小时44分 

C. 7小时

D. 6小时48分

5. 春节期间，甲、乙、丙三个人用支付宝钱包玩发红包游戏，只能通过各自账户余额来发红包，第一轮甲给乙的红包金额等于乙支付宝钱包里面的账户余额，甲给丙的红包金额等于丙支付宝钱包里面的账户余额，与此相同，第二轮乙给甲和丙的红包金额等于他们各自支付宝钱包的账户余额，第三轮丙给甲和乙的红包金额等于他们各自支付宝钱包里面的账户余额，若最后大家支付宝钱包里面的余额都是16元，则甲最初的支付宝钱包账户余额为（ ）

A. 24

B. 26 

C. 28

D. 30

6. 阿里巴巴启用了新的办公大厦，这里的一切都充满了现代感；工程师们打算在娱乐区用大小相等的圆形材料分割出一些空间，使用A,B,C三个圆形材料，最多可以将空间分为八个区域（包括圆形以外的区域），如果给你五个圆形材料，你最多可以帮助工程师们分出多少个空间（ ）

A. 20

B. 22

C. 26

D. 32

7. 七个人并排站成一排，如果甲乙两个必须不相邻，那么不同排法的种数是（ ）

A. 1800种 

B. 2400种

C. 3600种 

D. 1200种

8. 20个阿里巴巴B2B技术部的员工被安排为4排，每排5个人，我们任意选其中4人送给他们一人一本《effective c++》，那么我们选出的4人都在不同排的概率为（ ）

A. 5^4*5!*15!/20!

B. 4^5*5!*15!/20!

C. 5^4*4!*16!/20! 

D. 4^5*4!*16!/20!

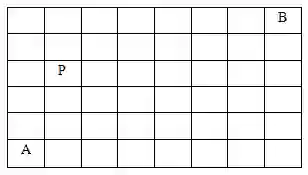
9.在如下6*8的矩阵中，请计算A移动到B一共有（ ）种走法。要求每次只能向上或向右移动一格，并且不能经过P。

A. 568

B. 626

C. 680

D. 702

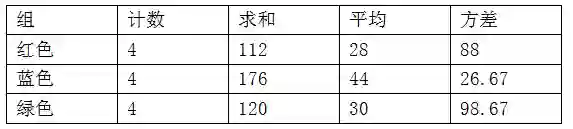
10.为了考察不同包装颜色对某商品的销量是否影响，随机选定了3家所在区域与规模都近似的超市进行实验，每家超市分别只销售一种包装颜色的该商品，实验期为4周，搜集数据后用EXCEL进行方差分析，所得结果如下表，则对此数据表述不正确的是( )

方差分析：单因素方差分析

SUMMARY

方差分析

A. 该实验的原假设是红色、蓝色、绿色三种产品的平均销量无显著差异

B. 在5%显著水平下，可以认为颜色对销量有显著的影响

C. 在5%显著水平下，可以认为红色销量明显低于其它两种颜色

D. 在5%显著水平下，至少两种颜色销量之间有显著差异

— 天团讲师 —

— 课后答疑 —

< 机器学习中的数学班 >

2月10日（本周六）开课。包含：微积分、概率论、线性代数、优化、机器学习五大阶段。直播＋录播的形式，长期有效。并配有私密答疑群，切切实实地带领大家学会学懂，夯实基础。

课程特点

相比第一期的主要改进：

硬性条件大力提升—杜绝因麦克风、手写板、语速过快导致的上课体验不佳；

讲清楚每个知识点—杜绝堆砌知识、罗列结论，重点阐述来龙去脉、因果为何；

通俗易懂更成体系—站在初学者的理解和接受程度，一步步循序渐进，厘清整个机器学习所需要掌握的数学体系；

加强作业测评巩固—每次课均布置作业，且最后设置考核；

讲师团队再次升级—管、孙、唐三大博士 + 寒老师坐阵，既通晓本质，更透析应用。 

课程内容

机器学习中的数学第二期

第一阶段  微积分

第一课：微分学基本概念

知识点1：极限，导数，偏导数，泰勒级数 

实战项目：梯度下降法与牛顿法

第二课：微分学进阶

知识点1：函数求导法则，反函数求导，隐函数定理简介

实战项目：反向传播算法在神经网络里的应用

第二阶段  概率论

第三课：概率论简介

知识点1：积分学与概率论基本概念，贝叶斯公式，正态分布与熵

实战项目：朴素贝叶斯分类器

第四课：极大似然估计

知识点1：极大似然估计，凸函数，琴生不等式

实战项目：逻辑回归，EM算法简介 

第三阶段  线性代数

第五课： 线性代数基础

知识点1：线性函数与矩阵运算

实战项目：最小二乘法的几何以及统计学意义 

第六课：线性代数进阶

知识点1：矩阵标准型理论简介，矩阵的奇异值分解

实战项目：数据降维之主成分分析

第四阶段  优化

第七课：凸优化简介

知识点1：凸优化问题，拉格朗日乘数法与KKT条件

实战项目：从优化的角度理解支持向量机

第八课：优化的稳定性

知识点1：Ridge优化算法 与 Lasso优化算法

实战项目：压缩感知与图像处理简介

第五阶段  机器学习

第九课：从线性模型谈起的机器学习分类与回归

知识点1：线性回归、逻辑回归、softmax、hinge loss、cross-entropy loss

知识点2：神经网络与非线性切分

实战项目：线性分类器与神经网络的非线性切分案例

第十课：从信息论到工业界最爱的树模型

知识点1：信息熵、信息增益、信息增益率、gini index

知识点2：ID3、C4.5、CART、随机森林、GBDT

实战项目：用决策树与随机森林完成分类案例

更多课程内容，扫码了解↓↓↓