无监督学习才不是“不要你管”
| 全文共3017字,建议阅读时4分钟 |
原作:Justin Gage
虚无之栗 编译自 Algorithmia
转载自公众号:量子位
微信号:QbitAI
如果你的一大坨数据没。有。标。签,怎么办?
无监督学习是机器学习算法里非常扑朔迷离的一个类别,负责解决这些“没有真实值 (no-ground-truth) ”的数据。
本文会讲到,无监督学习到底是什么,和机器学习的其他算法有何本质区别,用的时候有哪些难点,以及推荐阅读的传送门。
无监督学习是什么?
最简单的理解方式,就是把算法想象成考试。卷子上的每道题对应一个答案,得分高低就要看你的答案和标准答案有多接近。不过,如果没有答案只有问题,你要怎么给自己打分?
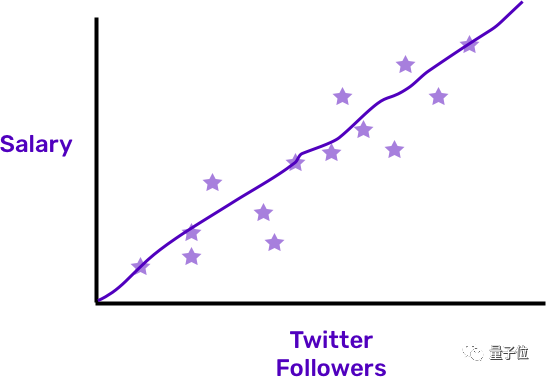
把这一套东西挪到机器学习上来。传统的数据集都有标签 (相当于标答) ,逻辑是“X导致Y”。比如,我们想要知道,推特上粉丝更多的人,是不是收入也更高。那么,input是粉丝数,output是收入,要试着找出两组数据之间的关系。
每颗星是一个数据点,机器学习就是要画出差不多能连起那些点的一条线,以此解释input和output之间的关系。但在无监督学习里,并没有output这个东西。
我们要做的是分析input,也就是粉丝数。但没有收入,或者Y。就像是考试只有题,没有标答一样。
其实,也不一定是没有Y,可能我们只是没有办法获得收入数据。不过这都不要紧,重要的是不需要画出X和Y之间的那条线了,不需要找它们之间的关系了。
那么,无监督学习的目标是什么?如果只有input没有output,我们到底该怎么办?
无监督学习分几种
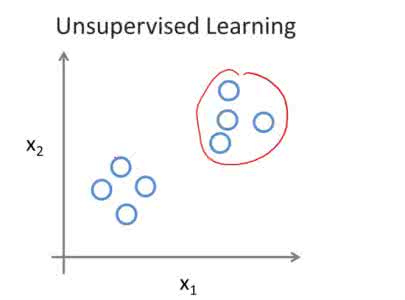
聚类(Clustering)
任何行业都需要对用户的理解:他们是谁?是什么促使他们做出购买的决定?
通常,用户可以按照某些标准分为几组。这些标准可简单如年龄如性别,也可复杂如用户画像、如购买流程。无监督学习可以帮我们自动完成这个任务。
聚类算法会跑过我们的数据,然后找出几个自然聚类 (Natural Clusters) 。以用户为例,一组可能是30多岁的艺术家,另一组可能是家里养狗的千万富翁。我们可以自己选择聚类的数量,这样就能调整各个组别的粒度 (Granularity) 。
有以下几种聚类方法可以选用:
· K-Means聚类,把所有数据点划分到K个互斥组别里。复杂之处在于如何选取K的大小。
· 层次聚类 (Hierarchical Clustering) ,把所有数据点划分到一些组别、和它们的子组别里,形成像族谱一样的树状图。比如,先把用户按年龄分组,然后把各个组别按照其他标准再细分。
· 概率聚类 (Probabilistic Clustering) ,把所有数据点按照概率来分组。K-Means其实就是它的一种特殊形式,即概率永远为0或1的情况。所以这种聚类方式,也被亲切地称为“模糊的K-Means”。
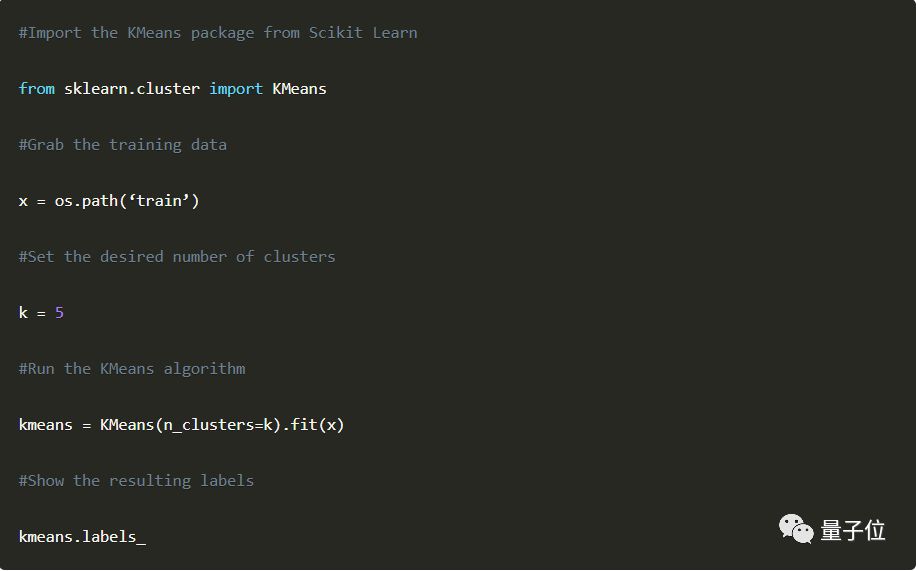
这几种并无本质区别的方法,写成代码可能就长这样——
任何聚类算法的output,都会是所有的数据点、以及它们所对应的组别。这就需要我们自己来判断,output代表怎样的含义,或是算法到底发现了什么。数据科学的魅力即在于,output加上人类的解读,便会产生价值。
数据压缩 (Data Compression)
在过去的十年间,设备的计算能力和存储能力都增强了许多。不过,即便在今天我们依然有理由,让数据集尽可能小、并尽可能高效。这意味着,只要让算法去跑一些必要的数据,而不要做过多的训练。
无监督学习可以用一种名为数据降维 (Dimentionality Reduction) 的方式做到这一点。
数据降维的“维”,就是指数据集有多少列。这个方法背后的概念和信息论 (Information Theory) 一样:假设数据集中的许多数据都是冗余的,所以只要取出一部分,就可以表示整个数据集的情况了。
在实际应用中,我们需要用某种神秘的方式,把数据集里的某些部分结合到一起,来传达某些意义。这里有我们比较常用的两种降维方式——
· 主成分分析算法 (PCA) ,找出能够把数据集里的大多数变化联系起来的线性组合。
· 奇异值分解 (SVD) ,把数据的矩阵分解成三个小矩阵。
这两种方法,以及另外一些更复杂的降维方式,都用了线性代数的概念,把矩阵分解成容易消化的样子,便于传递信息。
数据降维可以在机器学习算法里,起到非常重要的作用。以图像为例,在计算机视觉里,一幅图像就是一个巨大的数据集,训练起来也很费力。而如果可以缩小训练用的数据集,模型就可以跑得更快了。这也是为什么,PCA和SVD都图像预处理时常见的工具。
无监督深度学习
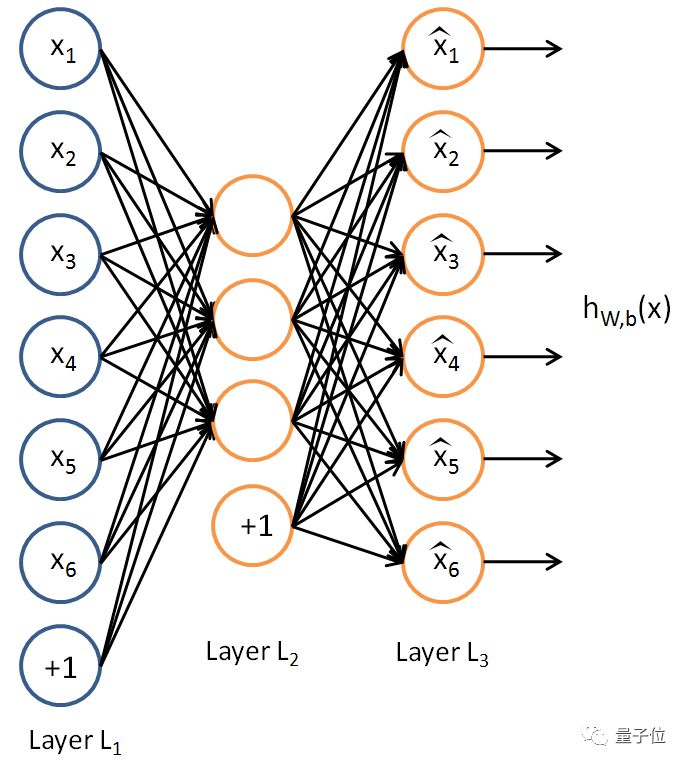
无监督学习,把领地扩张到了神经网络和深度学习里,这一点也不奇怪。这个领域还很年轻,不过已经有了自编码器 (Autoencoder) 这样的先行者。
自编码器和数据压缩算法背后的逻辑差不多,用一个子集来反映原始数据集的特征。像神经网络一样,自编码器利用权重把input转换成理想的output。不过在这里,output和input并不是两种不同的东西,output只是input的一种更轻便的表示方式。
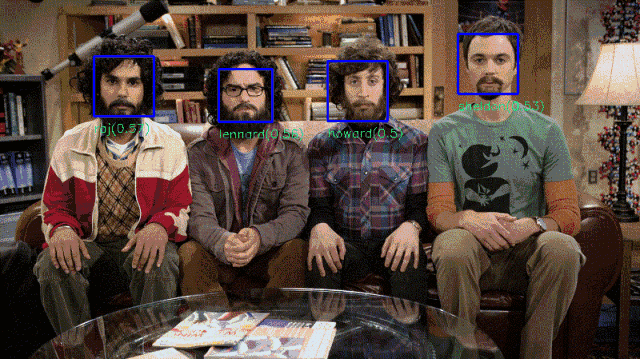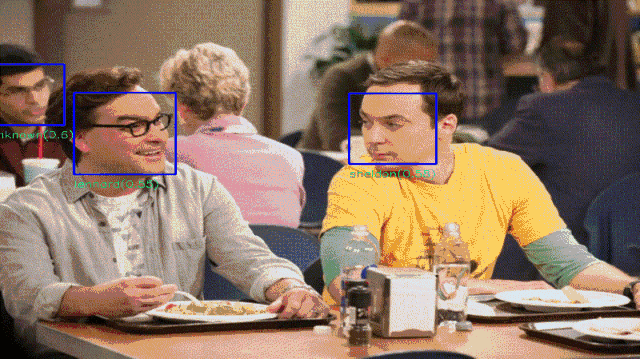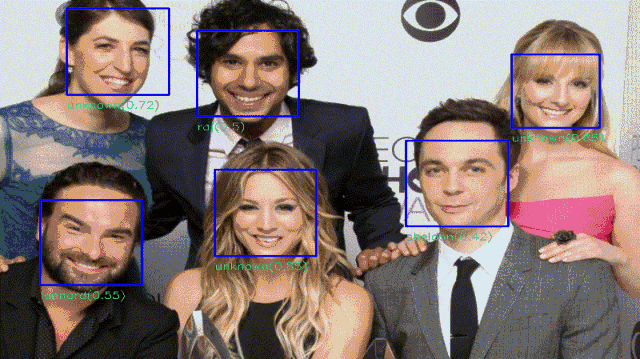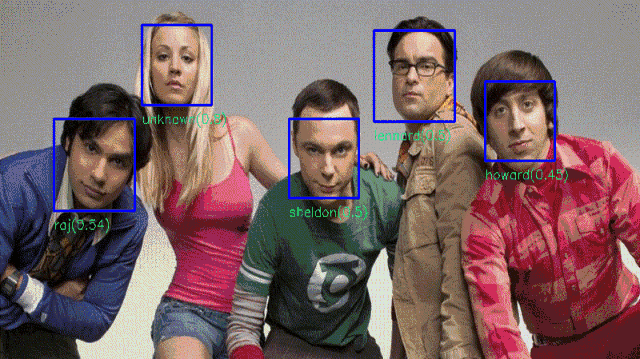
在计算机视觉中,自编码器被用在图像识别算法里。现在,它也已经把触角伸向声音和语音识别等更多的领域。
实战难点有哪些
除了寻找合适的算法和硬件,这样常见的问题之外,无监督学习自带一种神秘的气质——不知道任务到底完成了没有。
在监督学习里,我们会定下一套标准,以做出模型调试的决策。精确度 (Precision) 和查全率 (Recall) 这样的指标会告诉我们,现在的模型有多准确,然后我们可以调整参数来优化模型。分数低,就要继续调。
可是,无监督学习的数据没有标签,我们就很难有理有据地定下那套衡量标准。以聚类为例,怎么知道K-Means的分类好不好 (比如K值取的合不合适) ?没有标准了,我们可能就需要有点创造力。
“无监督学习在我这里管用么?”是人们经常提出的问题。这里,具体问题要具体分析。还以用户分组为例,只有当你的用户真的和自然聚类相匹配的时候,聚类的方法才有效。
虽然有些风险,但最好的测试方法,可能就是把无监督模型放到现实世界里,看看会发生什么——让有聚类的和没有聚类的算法做对比,看聚类能不能得出更有效的信息。
当然,研究人员也在尝试编写,自带 (相对) 客观评判标准的无监督学习算法。那么,栗子在哪里?
友好的传送门:
https://blog.algorithmia.com/introduction-to-unsupervised-learning/
下拉至Reading and Papers,栗子可能要从那里开始吃。
喜欢我们就多一次点赞多一次分享吧~
有缘的人终会相聚,慕客君想了想,要是不分享出来,怕我们会擦肩而过~