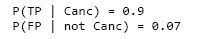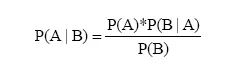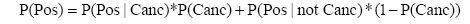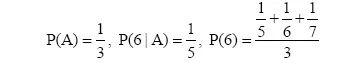条件概率与贝叶斯统计

2018 年 6 月 22 日 图灵教育

迄今为止，我们使用的统计方法在统计学中都称为频率论方法。我们从样本中得出的结论完全基于数据的频率或比例。这是最常用的一种推理框架，已经发展成为一种非常成熟的理论，主要内容包括本书前面介绍过的假设检验和置信区间。从原则上说，这种方法的优点是无偏性，结论仅仅建立在观测到的数据之上。但是，某些情况更适合使用另外一种统计方法：贝叶斯统计。

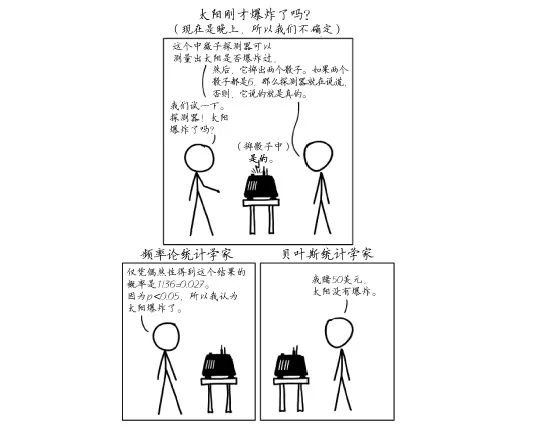
图1 太阳爆炸了吗？

图 1 中画的是什么情况呢？频率论统计学家很清楚，只有两种可能：探测器掷出一对 6，表示它说了谎；或者掷出其他的数，表示它说的是真的。因为没有掷出一对 6 的概率是 35/326（97.22%），所以频率论统计学家得出结论，探测器可能说的是真话。因此，太阳真的可能爆炸了。

贝叶斯统计学家在建立概率模型时会加入额外的信息。他也认为探测器不太可能掷出一对 6，然而，他主张要将探测器说真话的概率与太阳没有爆炸的先验概率进行比较。这位贝叶斯统计学家最终认为，太阳没有爆炸的概率比 97.22% 还要大，并决定赌一把“太阳明天照常升起”。

1.条件概率

构成贝叶斯推理基础的核心思想就是条件概率。在以前对概率的讨论中，我们依赖于一种前提假设，即事件都是独立的。例如，我们会这样假设，抛出一枚硬币的结果是正面还是反面，与上一次抛掷的结果是正面还是反面无关。这种假设对于数学计算非常方便，但生活并不总是这样。在很多实际情况中，独立性是个糟糕的假设。

考虑一下随机选择出一个体重超过 180 磅的美国成年男性的概率。男性的概率为 0.5，体重超过 180 磅（美国人的平均体重）的概率也大约是 0.5。所以，如果这两个事件是独立的，那么找出一个既是男性体重又超过 180 磅的人的概率就是 0.25。但是，这两个事件不是独立的，因为美国男性的平均体重要比女性多 30 磅。所以，这个问题应该是这样的：(1)选择一个男性的概率是多少；(2)如果选择出来的人是男性，那么这个人的体重超过 180 磅的概率是多少。使用条件概率的表示方法可以更容易地表述这个问题。

P(A|B) 表示当 B 为真时，A 为真的概率，它经常读作“给定 B 时，A 的概率”。因此，公式：

P(male)*P(weight > 180 | male)

准确表达了我们要找出的概率。如果 P(A) 和 P(B) 是独立的，那么 P(A|B) = P(A)。对于前面的例子，B 表示男性，A 表示体重>180。一般地，如果 P(B) ≠ 0，则：

P(A|B) =P(A+B)/P(B)

与一般的概率一样，条件概率也位于 0 和 1 之间。而且，如果 A 表示 not A，那么 P(A|B) + P(|B) = 1。

人们经常错误地认为 P(A|B) 等于 P(B|A)，但这种想法是完全站不住脚的。例如，P(male|Maltese)的值大约等于 0.5，但 P(Maltese|male) 只有大约 0.000064。

实际练习：估计一下随机选择一个体重大于 180 磅的美国男性的概率。假设美国人口的 50% 是男性，而且美国男性的体重服从均值为 210 磅、标准差为 30 磅的正态分布。（提示：可以考虑使用经验法则。）

公式 P(A|B, C) 表示当 B 和 C 同时成立时，A 成立的概率。假设 B 和 C 是互不相关的，那么通过条件概率的定义和独立概率的乘法法则可知：

P(A | B, C)= P(A, B, C)/ P(B, C)

这里的 P(A, B, C) 表示 A、B 和 C 同时为真的概率。同样地，P(A, B|C) 表示当 C 为真时，A 和 B 同时为真的概率。假设 A 和 B 是互不相关的，那么：

P(A, B | C)=P(A | C)*P(B| C)

2.贝叶斯定理

假设一个四十多岁的没有临床症状的女性做了一次乳腺X光检查，然后收到了一个坏消息：检查结果是“阳性”。

患有乳腺癌的女性通过乳腺 X 光检查确诊的真阳性概率为 0.9。而没有患乳腺癌的女性通过乳腺 X 光检查误诊为乳腺癌的假阳性概率为 0.07。

我们可以使用条件概率表示以上的事实。令：

使用这些变量，我们可以得到如下条件概率：

知道了这些条件概率，那么一个年过不惑的女性应该如何面对阳性的乳腺 X 光检查结果呢？她确实罹患乳腺癌的概率是多少？因为假阳性率是 7%，所以概率应该是 0.93 吗？还是应该比这个大，抑或比这个小？

这个问题很复杂：我们没有提供足够的信息可以使你给出一个合理的解答。要回答这个问题，你需要知道年过四十的女性罹患乳腺癌的先验概率。对于四十多岁的女性来说，患有乳腺癌的比例是0.008（1000 个人中有 8 个）。因此，没有乳腺癌的比例是 1-0.008 = 0.992。也就是说：

现在我们已经有了足够的信息，可以解决年过四十的女性所担心的问题了。要计算出她患有乳腺癌的概率，我们需要使用贝叶斯定理（通常称为贝叶斯定律或贝叶斯法则）：

在贝叶斯统计中，概率测量的是可信度。贝叶斯定理表明了不考虑证据的可信度和考虑了证据的可信度之间的关系。公式等号左边的部分 P(A | B) 是后验概率，即考虑了 B 之后的 A 的可信度。后验概率定义为先验概率 P(A) 与证据 B 对 A 的支持度的乘积。支持度是 A 成立的情况下 B 成立的概率与不考虑 A 时 B 成立的概率的比值，即：

P(B| A)/ P(B)。

如果使用贝叶斯定理来估计那位女性确实患有乳腺癌的概率，我们可以得到（Canc 即贝叶斯定理中的 A，Pos 则是 B）：

检查结果为阳性的概率为：

所以，

也就是说，大约 90% 的乳腺X光检查阳性结果都是假阳性！在这里，贝叶斯定理能够起作用的原因就是，我们对四十岁以上的女性患乳腺癌的概率有一个准确的估计。

请一定记住，如果先验概率是错的，那么估计后验概率时，只能使估计结果更坏，而不是更好。举例来说，如果开始时的先验概率为：

那么我们会得出假阳性率大约为 5%，也就是说，四十岁以上的女性在乳腺 X 光检查结果为阳性的情况下，患有乳腺癌的概率是 0.95。

实际练习：你正在森林中漫步，突然发现一片看上去非常鲜美的蘑菇。你采了满满一篮蘑菇，准备回家为丈夫准备一顿丰盛的晚餐。但是，在烹制蘑菇之前，丈夫建议你找本关于本地蘑菇种类的书参考一下，看看它们是否有毒。这本书说，在本地的森林中，80% 的蘑菇都是有毒的。然而，你将你采的蘑菇与书中图片里的蘑菇对比了一下，确定有 95% 的把握可以认为你的蘑菇是安全的。那么你是否应该将蘑菇做给丈夫吃（如果你不想成为寡妇的话）？

3.贝叶斯更新

通过应用贝叶斯定理，贝叶斯推理提供了一种理论方法，可以使用新的证据修正先前的可信度。贝叶斯定理可以迭代使用：观测到一些新证据之后，可以将原来的后验概率作为先验概率，并根据新的证据计算出新的后验概率。这使得贝叶斯定理可以应用在各种类型的证据上，无论是一下子同时出现的证据，还是随着时间推移逐渐出现的证据。这个过程就称作贝叶斯更新。

我们看一个例子。假设你有一个袋子，其中装有相同数量的三种骰子，每种骰子掷出6的概率都不一样。A 类型的骰子掷出 6 的概率是 1/5，B 类型的骰子掷出 6 的概率是 1/6，C 类型的骰子掷出 6 的概率是 1/7。把手伸进袋子，抓出 1 个骰子，并估计这个骰子是 A 类型的概率。甚至不需要很多概率知识你就可以知道，这个概率的最优估计值是 1/3。然后，掷两次骰子，并根据结果修正你的估计。如果每次都掷出 6，那么很明显这个骰子是 A 类型的可能性要更大一些。那么这个更大的可能性是多少呢？我们可以使用贝叶斯更新来回答这个问题。

根据贝叶斯定理，第一次掷出 6 后，这个骰子是 A 类型的概率为：

P(A | 6)=P(A)*P(6 | A)/ P(6)

其中：

图2中的代码实现了贝叶斯定理，并使用这个定理计算出骰子是 A 类型的概率。请注意，第二次调用 calcBayes 函数时，使用了第一次调用的结果作为 A 的的先验概率。

图2 贝叶斯更新

贝叶斯更新运行这段代码，会输出：

可以看出，这个概率估计的修正值是一直上升的。

那么，如果两次投掷都没有掷出 6，会是什么情况呢？将图 2 中的最后 4 行代码替换为以下代码：

会输出：

可以看出，这个概率估计的修正值在一直下降。假设有理由相信袋子中 90% 的骰子都是A类型，只需将原来代码中的先验概率 priorA 修改为 0.9 即可。这样，如果模拟两次投掷都没有掷出 6 的情况，代码会输出：

可见，先验概率有多么重要！

我们再做一个实验。仍然保持 priorA = 0.9，看看如果抓出的骰子实际上是 C 类型会发生什么。图 3 中的代码模拟了掷 200 次 C 类型的骰子（它掷出 6 的概率是 1/7），然后在每 20 次投掷之后，对这个骰子是 A 类型的概率进行一次修正，并输出修正后的估计值。

图3 对较差先验概率的贝叶斯更新

对较差先验概率的贝叶斯更新运行这段代码，会输出：

好消息是，即使是在给定了一个有误导性的先验概率的情况下，当试验次数逐渐增加时，后验概率还是逐渐收敛于真相。顺便提一句，我们还要注意，这个过程不是单调收敛的。120 次投掷之后的概率要高于 100 次投掷之后的概率，说明这 20 次投掷更符合骰子是A类型的情况，而不是 B 类型或 C 类型。

如果我们从一个更好的先验概率开始，后验概率会收敛得更快。如果回到 1/3 的初始先验概率，那么在 100 次投掷之后，后验概率就收敛到了 0.0335；在 200 次投掷之后，则收敛到 0.0205。

本文内容摘自《Python编程导论（第2版）》，作者 John V. Guttag 是 MIT 最受欢迎的教授之一。加塔教授的计算机科学课，MIT 6.00SC Introduction to Computer Science and Programming 第一堂在油管的观看量已经接近 60 万。本书以 Python 3 为示例，基于 MIT 热门 MOOC 教程编写，旨在培养读者计算机思维，为其日后的 IT 生涯打下坚实的编程基础。