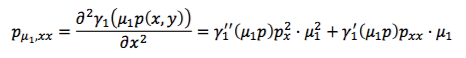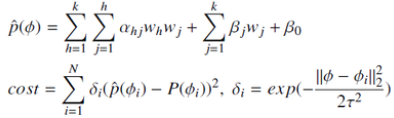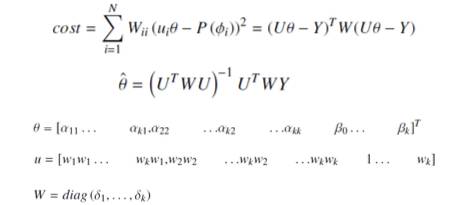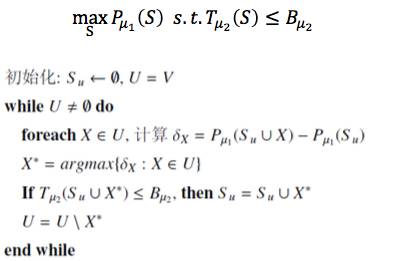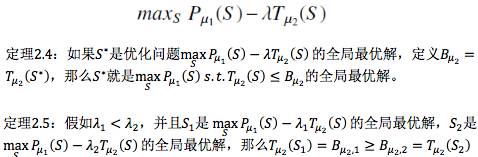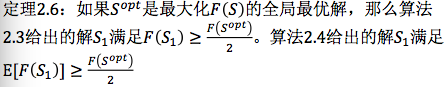优化神经网络模型结构新方法 | 清华张长水云栖大会分享

2017 年 10 月 17 日 数据派THU

回顾姚期智院士云栖大会演讲干货：姚期智云栖大会首日演讲：为什么我说现在是金融科技的“新”黄金时代

10月14日的阿里云栖大会机器学习峰会专场上，与会嘉宾共同探讨机器学习的前沿与挑战。清华大学自动化系张长水教授为大家带来“神经网络模型结构优化”的主题演讲，分享了神经网络模型结构优化的新办法，并解析实验过程、效果及应用案例。

张长水，智能技术与系统国家重点实验室学术委员会委员，清华大学自动化系教授、博士生导师，清华-青岛数据科学研究院二维码安全技术研究中心主任。主要从事机器学习与人工智能、计算机视觉等研究工作。

数据派整理了张长水教授此次的演讲干货，后台回复关键词“1014”下载完整版PPT。

以下是张长水教授演讲实录：

今天我和大家分享的主题是“神经网络模型的结构优化”。我大概会讲这么几点：

研究背景
子模函数和超模函数
神经网络结构的优化
实验部分

研究背景

当前，深度神经网络模型给我们带成了很大的影响，深度学习模型在传统的很多机器学习问题上，都取得了令人瞩目的突破和进展。

我举一个例子，比如图像识别。图像识别是这样一个问题：有一张图像，需要识别这个图像是猫、是狗、是计算机、是羽毛球拍？在2012年，深度学习网络用于解决该问题时，有了很大的突破。

除此之外还有其他的问题，比如图像描述、机器翻译、语音识别。机器翻译我们知道过去几十年发展也很慢，基本上没有办法应用实际，也是因为深度学习方法的应用，使得机器翻译有了一个很大的突破。百度因为这个方面的工作，大概在去年获得了一个国家科技进步二等奖，是王海峰带领他的团队的成果。此外，语音识别，大家都知道，以前也是没有到应用的水平，而现在我们就可以用。比如说大家用微信，就可以用语音输入。目前为止性能还不错的语音识别系统，全部都是用深度学习方法去做的。除此以外还有很多，比如医疗。还比如大家都知道的下棋。

深度学习方法应用有很多好处，同时也有很多问题。比如说，深度学习网络模型计算量特别大、模型特别复杂。模型复杂导致两个问题，第一是训练上的困难，第二个是测试上的困难。

训练上的困难在于它需要大量的时间，而且一个深度学习网络要想在某个问题上达到特别好的实用化性能，需要特别多的数据。而这对于机器计算的要求、对于数据的要求，通常来说不是我们在高校擅长做的。因此，工业界就显得很有优势，他们有数据、有计算资源。

现在深度学习的技术进步了，但是训练模型依然要花费很长时间。像我们实验室动不动训练一个模型就要一两天的时间。另外测试时间也很长，我给一个数据，跑神经网络，最后从末端给出一个结果。这个过程看起来只有一遍过程，但是由于中间计算过于复杂，所以时间仍然很长。比如给一张图像，通常来说如果代码写的不够好，大概需要几秒的时间，如果写的特别糟也可能一分钟的时间。可是我们知道有些应用问题不允许你这样做，它需要你实时地识别图像。

还有就是对内存有要求。神经网络模型有大量的参数都要存到计算机里去。如果你用的是服务器，这就没问题，但当你的这个技术走向应用变成产品，这就不一样了。比如说无人驾驶车，我们希望无人驾驶车上装的摄像头能够识别路上的情况、标识一些物体，你如果这么做，就要在无人驾驶车上有一个识别设备。我们知道无人驾驶车是一个那么有限的环境，它不太可能让你放一个服务器或GPU，所以它的计算能力很弱。

还有就是它对于电的要求高，我们知道GPU特别费电，车上不太可能放一个几百瓦、上千瓦的供电系统。所以有人对AlphaGo的一个批评就是，你和人去比赛，人靠的是什么，喝一杯牛奶、一片面包、一个鸡蛋就来参加比赛；AlphaGo靠什么，后面有那么大的一个供电系统。还有一个特别理想的状况，既然深度学习做图像识别已经有了很多突破，为什么不用在手机上？可是一旦考虑用在手机上，就发现有一堆的问题：内存太小、计算能力太弱、耗电太厉害，所有这些东西都导致了神经网络现在在应用阶段有非常大的困难。

因此就提出这样的问题，我们怎么样让深度学习网络紧凑、小型化。在实际中，我们做深度学习的时候有一个很重要的问题，就是要调参数。首先，给你一个问题，你有了数据，选择了一个基本模型，但是这个模型结构到底怎么设置，层有多少，每层宽度多少？这样一些参数怎么去定？有很多的因素会影响我们学习的性能。

有人做过一项这样的研究，你能够把网络学的好，学习率（learning rate）是最重要的一个因素。学习率就是我们求偏导的时候，会对导数的权重调整的系数，这个系数特别重要，有相当多的研究工作关注在这个地方，这个地方任何一个突破对所有人都是至关重要的，这里“所有人”是指对神经网络使用的那部分研究人员。此外，每层的宽度也是一个重要的参数。我今天的报告主要讲如何选择每层宽度。

神经网络结构优化，有哪些已有的方法？

贝叶斯方法

权重参数是我们在训练阶段要学习的一个参数，此外我们需要提前确定的参数我们叫超参数。我们在超参数这个问题上怎么去做？这是我们传统的深度学习、机器学习比较关注的问题。我们假设有一个要学习的参数，有的时候我们给这个参数假设一个形式，例如：高斯分布，那这个高斯分布就是你的先验，你再想办法确定这个高斯分布的均值、方差。这就是贝叶斯方法。但是这样的方法里面，你需要先确定先验。

导数的方法

优化目标函数通常的做法是通过求导完成的。我们往往对神经网络的权重进行求导。既然你的学习率是一个超参数，我们为什么不能够对它进行学习？所以如果你能够建立你要优化的这个损失函数和你现在要学习的超参数之间的函数关系，建立这个函数关系以后，就可以去求梯度、求导。这个方法的优点是很明显的，但是缺点就是，可能需要你把这两者之间的函数关系理清楚。第二个，对于离散的问题，这种办法就不好用。

网格搜索

超参数还怎么优化？在实际过程中我们还有一些经验上的做法，比如说网格搜索。大家去设想一下，在神经网络之前我们大家学过支持向量机。支持向量机的目标函数有两项：是间隔项和惩罚项。这两项之间会有一个C来平衡大的间隔和错分样本的惩罚。这里 C是需要提前定的。但是实际中我们不知道C是多少。实际做的过程就是，我们通过网格搜索把这C等间隔取值，分别优化SVM，使得我能够得到一个特别好的结果。调好参数很重要，一来你要去发文章的时候，把你的参数调的尽可能好，和其它最好的方法去比较。另一个就是调系统和产品，我们希望自己的系统性能尽可能好，去卖个好价钱。

假如我们要优化一个神经网络，而我只关心这两层的宽度。所谓的网格搜索就是，让每层的宽度取值5、10、15、20、25个节点，然后两层一起考虑，遍历所有的组合。这样做保证不丢掉一些重要的结构。可想而知，这种做法非常慢，而且我们神经网络往往会很多很多层，所以这是一个很头疼的事。

即使采用遍历的方法，网格搜索的方法后来也被认为不太好。在2012年Bengio在 “The Journal of Machine Learning Research”发表的工作告诉我们，假设你要优化的那两个参数，可能有一个很重要而另一个不那么重要，网格搜索就意味着构成一个这样的搜索点的分布，这个分布向两个方向投影，就意味着你搜索了9个点，而在每个方向上都有一些搜索点重复。如果我们采用随机采样的方式，而不是网格搜索的话，就有可能会充分利用这九个点采到这个特别重要的点。他们做了一些理论的和实验的分析，说明随机搜索效果往往会更好。而比较有意思的，随机搜索本身其实是一个很简单的过程，不需要那么多的预备知识和技术，所以是一件挺好的事。

结构优化是一个离散优化问题，所以我们用前边很多的贝叶斯方法、求导方法不能用，所以通常情况下，都是人工做的。如果我们在座的有老师，让你的学生去调参，说你要网格搜索，他可能会拒绝，他说这事我搞不定，这个参数组合太多了，另外，我们机器承受不了，我算一次就要1天、2天，我这样一组合可能要几百次、几万次人工调参数。所以人工调参数费时费力。

此外，就是需要特别多的知识，你要有很多的知识和经验才能调好参数，对专家的依赖性很强。更关键的问题是，我好不容易花一个月把参数调好，现在换一个数据集，我还需要再花半个月时间调参。另外是当你的应用场景发生变化的时候，新的客户来了，这个时候你不得不调，非硬着头皮做不可，所以熬夜就成了家常便饭。

其它优化手段

其一，低秩近似。我们把神经网络这些权列成一个矩阵，假设这个矩阵是低秩的，加上低秩正则以后，去优化这个网络结构。换句话说，在你优化整个目标函数的时候，同时希望这个秩要低。如果把约束加在全连接层上，效果就比较好。

其二，去掉无用的连接和节点。神经网络每相邻层之间都是连接，我们有的时候会问，所有这些连接都有用吗，是不是有的连接没有用？如果是这样的话，我们是不是可以把没有用的连接去掉。换句话说，看起来那个权重是有，但是其实很小，我们总觉得特别小的权重起的作用很弱，我们就把它去掉。

这种想法有人做过，就是我先训练一个网络，训练好以后，我看哪个权重特别小，把它去掉，然后再重新训练。训练稳定了以后，看哪个权重又小，再把它去掉，一点点这么去做。好像2015年NIPS会议上就有这样一个文章发表，大概用的是这样的思路。当然也有人说，我对于你们的权重加一个稀疏的正则，去优化。当然这样从做法上更流畅、更漂亮。后来有人说，除了连接很重要，中间有几十万个节点，每个节点都很重要吗，能不能把某个节点去掉，这个做法就是节点稀疏。

其三，量化权重。现在整个权训练好了，但是因为有很多权，我要存这些权就很麻烦，因此大家想，这个权重不用浮点数，用整数行不行？整数做的一种办法就是，把所有的权重都聚类，在聚集多的地方取值，其它的用近似。还有一种做法就是，把所有的权重量化成几个等级，比如有4个等级。一个极端是两个等级，有和没有，有的话就是1，没有的话就是0。在这种情况下你会发现，整个神经网络计算就变得非常非常的容易，只存在有和没有，就变得非常的简单和快速。

当然，所有这些方法都会带来副作用，就是你的识别率会下降。有的时候我们会说，我们关注这个算法能不能放手机里去，因为通常来说，放到手机里的很多应用程序对识别率没有那么高的影响，认为大众对有些识别问题的要求可能没有那么高。这样识别率降一点也没有特别大的关系。

子模函数和超模函数

子模函数和超模函数是后边的网络结构优化要用到的知识。介绍的时候我先说明，这里面大概有10页左右的PPT是从这个网站上拿过来的（网址：http://www.select.cs.cmu.edu/tutorials/icml08submodularity.html）。在2008年国际机器学习大会有一个特别好的tutorial，就是关于子模函数和超模函数。那个报告给我印象深刻，所以我就把其中的几页拿过来在上面做了一些改动。不管怎么说，谢谢这两个作者。课后大家如果对这个有兴趣，可以去看看他们很完整的PPT。他们对子模函数和超模函数介绍非常详细，很感谢他们。

子模函数和超模函数，是关于集合函数的一些性质。集合函数是指，这个函数是定义在它的子集上的函数，这个函数在每个子集上的取值。通常我们认为空集函数是对应的是0。

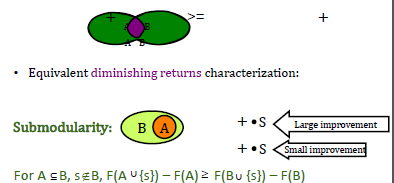
什么是子模函数？子模函数是怎么形成的，我们不去管它，可以把它看成一个黑箱（black box），但是我们希望这个函数具有一个这样的性质：对于任给的A、B两个子集， F(A)+F(B) ≥ F(A ∪ B)+F(A ∩ B)。

如果它满足这个条件，就说它是一个子模函数。这样的性质也等价于这个性质：有两个集合，一个是A，一个是B，A集合是B集合的一部分。这种情况下如果在A集合上加上一个元素，这个集合就变大一点，变大了以后，这个函数会比原来A集合函数增加了一部分，在小的集合上增加的量要更大大。换句话说，小集合加上一个元素带来的改进更大，而在大的集合上增加同样的元素以后，它带来的影响会比较小一些。

什么是超模函数？如果F是一个子模函数，前面加一个负号，那就是超模函数。

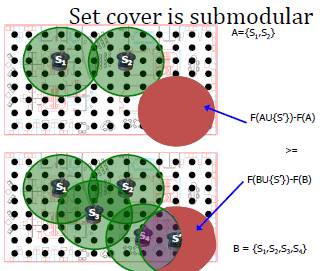
这件事有点太抽象，我们举一个具体的问题，这样大家就会有很直观理解。假设，现在有一个房间，我们需要在房间里布置一些传感器，布置传感器是为了对整个房间进行数据采样。每个每个传感器会有一个覆盖面积。我们希望放上有限的传感器，覆盖的面积越大越好。在这样一个问题里边，对于任何一个集合，F（A）=A能够覆盖的面积。所谓的A是什么呢？就是你放的传感器，因为每个传感器会放在一个位置上。

这个问题里的F是一个子模函数（我定义F是它覆盖的那个面积）。为什么呢？可以设想，我有两种情况，一种情况是我放2个传感器，还有一种情况是，我放4个传感器，其中包含了刚才的两个传感器。我在2和4个传感器的布局里，分别再加上同一个位置的1个传感器，那么你会发现上面小的集合情况（2个传感器）下带来的面积增加量比较大。而原来4个传感器的集合增加的面积部分比较小。这是一个非常直观的例子。

子模函数有一个很有意思的性质：假如Fi是子模函数，这个λi>0，它的正的线性叠加仍然是子模函数。就是在正的这种线性组合的意义上它是封闭的。

我们怎么去理解子模函数？对子模函数的寻优对应的是一个离散的优化问题，我们可能知道更多的是连续的优化问题。在连续优化问题里边我们比较喜欢的一个问题叫凸问题，就是说白一点，我们只有一个单峰。这种情况下找最大值相对比较容易。我们通过求偏导，原则上一定能找到最优值。但是到离散问题以后，什么是凸我们就不知道了。而子模函数类似于我们在连续问题里的凸函数。下面这个例子会呈现子模函数与凸问题的关系。

假设有一个这样的函数g，它是从整数到实数的一个映射，函数F定义在A集合上，这个子模函数怎么定义呢？它就定义成我这个集合的“大小”，把集合别的因素都去掉，只考虑它的大小。这样如果两个集合a是b的子集，那么 a的大小 < b的大小。这个函数的特点就在于，在小的地方增加一点所带来的增益，和在大的地方同样增加一点所带来的增益，前者要大。所以你也可以认为，子模函数是离散函数的一种凸性质。

当然你会说我们还有别的运算，比如说两个子模函数F1、F2，求最大，那还是子模函数吗？它的最大max(F1,F2)不一定是子模函数。它的最小，就是这两个子模函数取最小，min(F1,F2)一般来说也不一定是子模函数。

神经网络结构优化

我们做的这个神经网络结构优化工作的想法就是，希望让算法来优化网络宽度，而不是不要让人工来调。我们怎么做这个事呢？

首先，把我们刚才的结构优化问题变成一个子集上的优化问题，这样就往我们刚才谈到的子模函数靠近。我们再分析一下我们要优化神经网络的目标函数，它有什么样的性质？是一个子模函数吗？这里我们关心它的单调性和子模性。把这两个问题解决掉以后，我们再给优化一个算法，这个算法又简单、效果又好。这就是我们大致的思路。

1. 离散向量优化问题转化为子集选择问题

第一个要说明的是，我们优化的一个神经网络，不局限于一定是个全连接网络，它可以是一个CNN，也可以是一个RNN，也可以是一个LSTM。在实验部分我们对这些模型都做了实验。

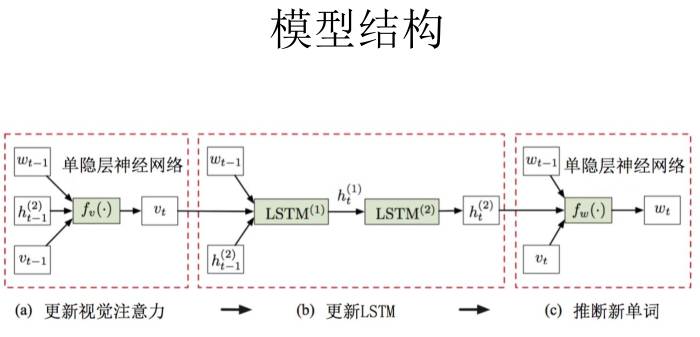
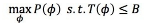
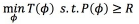
我们假设神经网络里每一层都有一个宽度，第一层的宽度W1，第二层的宽度W2……宽度表示这个隐含层的节点数。对于一个神经网络而言，我们关心的是要优化这个宽度参数𝜙，使得在一定计算量的要求下神经网络的识别率尽可能高，也就是性能尽可能好（）。或者，在识别率比较高的前提下，计算量要尽可能地小（）。当知道这个网络大概是什么样， 𝜙就是一个确定了宽度的网络结构。

我们把具有不同宽度的网络结构优化问题看做一个自己选择问题。

2. 分析目标函数的性质

我们看目标函数有什么样的性质。首先它具有单调性：𝑆A⊂𝑆B，那么𝑃(SA) <𝑃(𝑆B)。单调性就是这样的，如果我有两个网络，前者小于后者SA ⊂ 𝑆B，比如说都是两个神经网络都只有一层，一个是5个节点、一个是10个节点；或者大家都是两层，一个结构是5个、5个，一个是10个、10个，那么前者比后者小。

如果是这样的我们就有这样的性质，小的网络性能比大的网络性能来的差。这件事证明起来不困难。基本的证明想法就是，如果你在一个小模型得到了特别好的结果，然后我就把小模型放在大模型里面去，大模型其它地方都填0，从这个时候开始作为初始化重新优化，一定能够优化一个比它更好的结果。另外一个就是，大模型比小模型计算时间更多：SA ⊂ 𝑆B，那么T(SA) >𝑇(𝑆B)。

我们希望这个函数是子模函数，但是这不一定。因此，我们分析一下，什么样的条件可以保证一个函数是子模函数。

我们做了一件事：用一个样条函数，由已知的离散点插出这样一个连续函数。我们要求，在取到的整数离散点处和它的值是一样的。第二，它是单调的，中间光滑的。第三，它的二阶导数存在。这样要求，从技术上说并不困难满足。

下边我们说，就是性能和时间具有什么样的性质。我们看一下这两层的情况，假设我们可能只有这两层，包括x层和y这一层。假如我们要求P这个函数是一个子模函数，那么下面这个定理告诉我们这个函数应该要满足什么样的条件：

这个定理告诉你，对于任意的两层x、y，它的二阶导数（这个Pxx就是对x求二阶导数，这个Pyy是对y求二阶导数），都要小于0，如果满足这个条件就具备子模性。Px是什么意思？就是对x求导，这表示x这层的节点增加以后P的性能的变化。P的性能我们刚才已经说了，是单调的。也就是说，这一层网络变宽了以后，网络的识别率会好一点，所以这个Px表示的就是性能增加的程度。

Pxx是对Px求导。Pxx<0是说，这层网络增加一个节点网络的性能虽然会增加，但是随着这个宽度越来越大，性能增加的量会越来越小，也就是说增速下降。所以仍然是增加，但是速度下降了。我们可以直观理解这种情况，在神经网络里可能是这样，我这个网络已经很好了，宽度越增加，带来的性能的提升越来越少。Pyy<0指的是对于y这一层。Pxy<0指的是两层交叉的情况。

我们同样可以把这件事用于时间这个函数。同样我们也可以得到一个对称的性质，这个性质是超模性，因为时间和刚才的准确率刚好是反的。

我们直观理解上面这个事是对的。但是这还不够，因为我们还没有证明。但是我们希望这件事是对的，怎么办呢？我们就这样去做，你这个P导致那个插值函数未必是满足条件的，我们能不能对这个P做一个变换，变换以后的那个函数成为子模函数。

所以我们就做了一个函数变换，函数变换实际是在原来的函数上乘一个正数𝜇1，作用于𝛾这个函数，把它变换成一个子模函数。如果𝛾这个函数选择的好，例如是个单调函数，那么，P（）和P𝜇1这两个函数是单调的，所以在相同的地方取最大值，因此不影响我们优化问题结果。这个里面，𝜇 1, 𝜇2 正整数，𝛾1 ，𝛾 2单调递增函数。

这个变换是什么样呢？我们先对这个函数计算二阶导数：

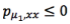
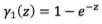
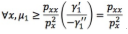
我们首先希望这个东西，令和。根据这个结果，我们就可以确定系数𝜇1。我们不仅对Pxx有要求，同时Pxy也要小于等于0，Pyy也要小于等于0，所以你选择的这个𝜇 1应该大于等于所有三个比值中最大的那个。我们有了这个式以后就知道了，这个变换𝜇应该怎么取。这么做就保证随便给我一个这样单调递增的函数就可以把它变成子模函数，这是一个有意思的事。

和这个变换对应的是一个饱和加强变换，就是说我能够使这个函数变得尽可能像一个子模函数，当然我们还有一种饱和减弱变换，就是如果你特别强，我们也可以让它变得弱一点。这里用了这样一个函数。

同样我们还得到了两个函数：发散加强变换和发散减弱变换。所以我们可以把一个函数变成子模函数，也可以变成超模函数。

我们怎么去估计𝜇值呢？因为刚才说了，我们用样条函数回归，从而得到插值函数。具体做法就是，已经知道了在某些点上P的值，用一个局部加权二次回归的办法得到一个连续函数：

这种连续的形式能保证刚才那几个条件，就是在那几个离散点上是和它值相等的，单调递增的，二阶导数是存在的。我们要优化的是这样的目标函数，我们希望这个目标函数最优。这是一个简单的回归问题，这个问题有一个闭式解。最后的解很简洁。

这件事告诉我们说，当你已经有了几个点以后，你可以非常明确地把这样的𝜇值算出来，你的𝛾变换是指定的，所以这个变换函数就已经有了，有了以后就告诉你说，你能保证这个P是子模函数、T是超模函数。

3. 提出算法并给出解的性质

在连续函数情况下，如果函数是凸的，优化的时候比较简单，就是你只要求偏导，就能得到一个最优值。离散情况下有点类似，如果它是一个子模函数，你用一个贪婪算法求解就可以。不一样的地方是，在连续问题下你能得到一个最优解，而在离散情况下你不一定能得到最优解。尽管这样，但是你能得到一个不错的解，你能得到一个性能有保障的解，这对我们来说已经很好了。比如我们前边给了大家几种优化的策略，那些优化策略，有的时候好、有的时候不好，好到什么程度你也不知道，差到什么程度你也不清楚，但是我们用这个方法就会有理论保证。

我们现在要优化这个问题，这里的优化的函数是子模函数，约束是一个超模函数。我们的算法是这样的，初始化可以从空集开始。所谓的空集并不是真的空，是我已经假设这一层最少比如说有10个节点，是从10开始的，而在这个地方空集就意味着从10开始的意思。我从空集开始往上加节点。我在当前的情况下去考虑增加一个节点或者几个节点，我增加进来以后，我看这个性能是多少，这个性能比刚才相比增加了多少，我算这个增加量。

算了增加量以后，你要考虑它有好几个可能性，我选一个最好的，比如我有三层，每一层都增加一个试一试，看在哪一层增加效果最好，你选出增加量最大的出来。这就是我在当前这一步选择的优化方向。你把这个放进来以后，你的子集就变得大一点，第一轮迭代就结束了。下面继续迭代。当然做这个事的时候，你要检查你增加进来这个节点以后，时间是不是小于这个B，是不是满足你的时间约束，不满足也不行。就这样逐步增加节点。这个算法是不是很简单？就是在各层上找一个节点，看看哪一个使得网络性能变革的最厉害，增加的量最大。

因为它是子模函数，所以我们就可以来分析它的性质。这个就是做机器学习的人特别关心的一件事，就是最好不要只给这个算法，说我这个算法好。你做一些实验是迫不得已的办法，如果你能给出一些理论分析就会觉得比较放心。我们这个定理就是这样的：

我有两个解，一个是整个网络能达到最好的解（全局最优），一个是我这个算法给出一个最优，这两个最优解之间差一个倍数关系，这个倍数关系你可以算一下。当然我们经验上来看，实际的优化的结果非常好。我们试过用这样的方法去解不同的问题。这个解是在满足这个约束时的解。这个约束的阈值B前面还有一个系数，这个系数通常来说是小于1的，也就是说它给出的这个解是比这个时间约束要更严格的一个情况下得到一个解，换句话说，这个解还没有那么好。如果时间多一点，解的性能可能会更好。

下面我们还可以给另一个算法，同样的问题，我们做法是这样的：

在这个算法中，不仅仅要算P的增加量，还要考虑时间的增加量，用这个比值来衡量那个增加哪个节点更划算。同样要求增加了节点，以后时间是满足这个要求的。

对于刚才这个算法我们也有一个类似的性能。当这个时间满足这个条件的时候，刚才的算法给出最优解S*，这个S*和全局最优解之间是这样的关系。这个解会比刚才算法的解更好。

这是刚才在有约束的情况下的算法。解这样优化问题的时候，其实还可以换一种思路去解，就是我们刚才那个约束优化问题写成这样一个形式。

就是把这个约束以一种这样的形式加到目标函数上去，如果是这样我们给这样一个结论，如果S*是原始优化问题的全局最优解，我们就知道S*同时也是这个无约束形式问题的全局最优解。

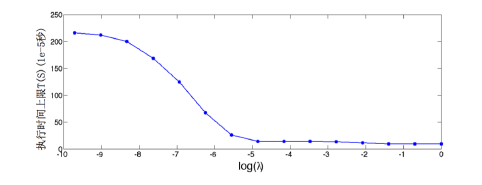
如果都是全局最优解，那么λ怎么取？如果我有两个λ，一个小一点，另外一个大一点，现在S1是这个问题的全局最优解，S2是这个问题的全局最优解，我们知道λ小的时候所对应的时间阈值更大。看这个图，λ变得越来越大的时候，上限会这样去降，刚开始会降的很厉害，到一定程度以后就已经降不大了。

在这种情况下，我们给出一个确定性的贪婪算法。这个算法是这样：刚开始是空集，增加一个节点，这个节点增加的时候，加进来算一算增加量是多少。我们还要考虑假设在整个节点上，性能减掉多少。相比一下看是不是值得增加，如果增加量这个a比较大，那就加上去。我们同样的得到一个和它对应的是另外一个算法，这个算法是我们需要算一个a的增加量和b的减少量，到底我要不要接收这个S，要以一定的概率来考虑，怎么叫以一定的概率呢？我们对于一个给Y变量，让它服从均匀分布，如果这个均匀分布采样得到这个值小于这个东西把这个加进去，这是一个随机的算法。

下面这个结论告诉说，刚才这里有两种算法，我可以给它一个理论保障，这个理论保障是这样的。如果这个So是整个这个问题的全局最优解，刚才第一个确定性的算法给出的解S1大于它的1/2， 2.4这个算法给出的解的数学期望是也是大于最优解的1/2。这样一来我们就知道这个算法有理论的下界，这件事告诉我们什么？你可以放心大胆的用这个算法。

看起来我们把所有事情都做完了。其实还差一点，我们要知道我们刚才一直在优化什么？我们刚才一直优化的全是这个东西，就是P𝜇1，把P做了一个子模变换以后的东西。其实我们训练一个网络，更关心的是原来的那个P。不过，因为这两者是一个一一对应关系。所以通过P𝜇1，P的对应关系，就可以得到真正的P。这件事情告诉我们什么呢？在这个函数变换中要乘𝜇1，可以乘得很大，也可以乘得很小。

如果乘的很小意味着你没有太多的变换因素。如果𝜇很大意味着增加了太多的变换因素，使得它变成一个子模函数，但是其代价是，得到的理论的下界变小了。所以𝜇1的取值不要那么任意，不要说越大越好，越大越是一个子模函数，对P𝜇1来说很好，但对于P来说没那么好。第一个极限的性质说，当𝜇1趋向于0的时候，就是一个最优值，如果𝜇1趋向于无穷，没有什么意义。

这里总结了一下，不论原函数是不是具有子模性还是超模性，你这个函数都可以做变换，使得变换以后的函数接近模函数。

当然还有其他的技术，例如使用替代函数加速探索新的区域。

实验部分

我们关心的是，在已有的数据集上我们的方法是不是比人工调出那个结构好。我们去看一下这个实验。在MNIST数据集上实验，也就是做手写数字识别。比较有意思的是，我们看这条虚线，对应的是LeNet，就是人们已经在数据集上仔细调出来的一个网络。我们可以知道我们的这些网络结构的准确率还能超过它。人调了半天得到一个结构，我们告诉你调的还是不够好，算法可以调的比你更好，就是这个意思。这个更好体现在什么地方？在同样的运行时间情况下，我得到的结构的识别率比你好。如果看相同的识别率的结构，我的结构比你少很多。

我们还是和已有的工作去比。在text8这个数据集上去做比较。

有人在这个上面去做识别率，它的网络结构是[256,256,256]，时间是144.5，单位时间是e的-5次方秒，它的性能，这个指标越小越好。我们用我们的算法自动调出一个结构，可以得到一个更快的模型，这个模型会比它更小，大概快了20%多。识别率差不多，因为我们要求速度要快。我们还有一个识别率更好的模型，就是时间和你差不多。

下面是在另外一个数据集上WMT，我们的算法和刚才是一样，要么同样的时间比你性能好，要么同样的性能下时间短。

下面是我们在做的另外两个问题，一个是交通标识识别。交通标识识别就是一个这样的问题，我们有一张图像，这些是我们关心的交通标识，我们需要识别这个交通标识的含义，比如这个是转弯、限速、往前走、停车等等。在交通标识这个问题上，其实如果你有了足够多的数据标注得很好，这个性能应该能达到还不错的性能，现在大家都能够做到。

但是这里边有一个问题，就是因为我们深度网络计算量特别大，而交通标识识别要用在无人车上。无人车要求算法一定要快。因为车以很快的速度往前跑，如果算法太慢的话，这个标志都过去了你才告诉我说“禁止停车”，这不让我犯错误嘛。我们说快到什么程度？原则上我们认为1秒钟15张图以上就算比较快。当然这依赖于你的车速，如果你的车开的速度更快，那么要求你每帧都识别出来了。

我们知道让算法识别一个标识，其实也不太慢。可是你面对的是整张图，通常来说你的视野下很多很多物体，有行人、有车、有交通标识，可能还有路面，还有树，还有商场。如果我们用现在的这种算法，我们需要先猜什么地方是交通标识，然后再去识别。比如说我们现在会有这样一个算法，先猜出2千个左右的候选，然后一个一个去识别。

假设1秒钟识别一个标识，那么这2千秒钟过去了。在这个应用中时间是大问题，就是怎么去加速是很重要的问题。可是这里边你又不太好去用GPU，因为汽车可能没有那么大的供电能力，他要求你的用电最好10瓦—20瓦。这个问题里边它对时间要求特别高。我们以前做过这个事，我们的算法非常快速，1秒钟能识别20张图像（不是20个标识）。

我们看看人工模型，人工模型【70、110、180、200】，计算时间是这样的，现在它的正确率是99.65%。我们的算法给出了两个更好的模型，一个是识别率更高，一个是速度更快。

再看另外一个问题，基于递归神经网络的图像描述算法。

图像描述是这样一个问题，给你一张图像，你给我生成一个句子来描述这个图像。原来的图像分类可以说是一个词，现在必须是一个句子。这两个其实会有本质的差异，后者更关注物体之间的关系。以前分类只是说，有人、有笔记本、有只鸟、有电线杆，仅此而已，但是并没有区分他们之间是什么关系。图像描述要说他们的关系，而且说关系的时候要自然语言描述，所以有很多不一样的地方。

解这个问题的模型非常复杂。这和我们做图像识别不一样。做图像识别我们有一些经验，大概知道怎么调参数，而这个问题其实我们根本不知道怎么调，我们都不知道哪个因素更关键，所以我们以前人工调的时候基本上不考虑时间，只要性能好就行。后来当然我们不断去调，调的还不错。现在可以用算法来调参数，给一个更准的模型，或更快的模型。

下面这是我生成的句子，你看看还是不错的，A man sitting at a table using a laptop，他坐在桌子上有一个笔记本电脑。这个a white plate topped with a half eaten sandwich，不仅仅说一个白盘子上面有一个三明治，还告诉你是咬了一半的三明治，这些细节都能抓得住。我们提出一个神经网络结构优化方法，这个方法比人工调整好，可以得到一个更好的模型，根据你的要求也许更快、也许准确率更高。