【普林斯顿Yuxin Chen】噪声矩阵补全的推理与不确定性量化，117页ppt

https://smartech.gatech.edu/handle/1853/61861

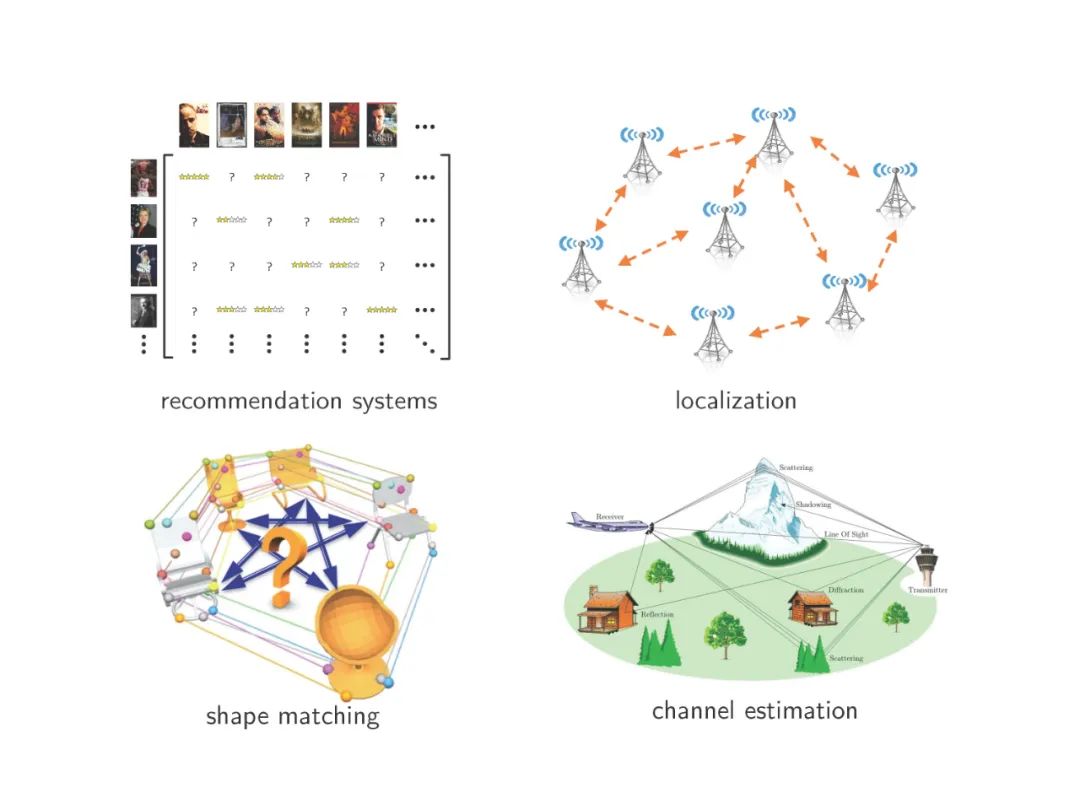
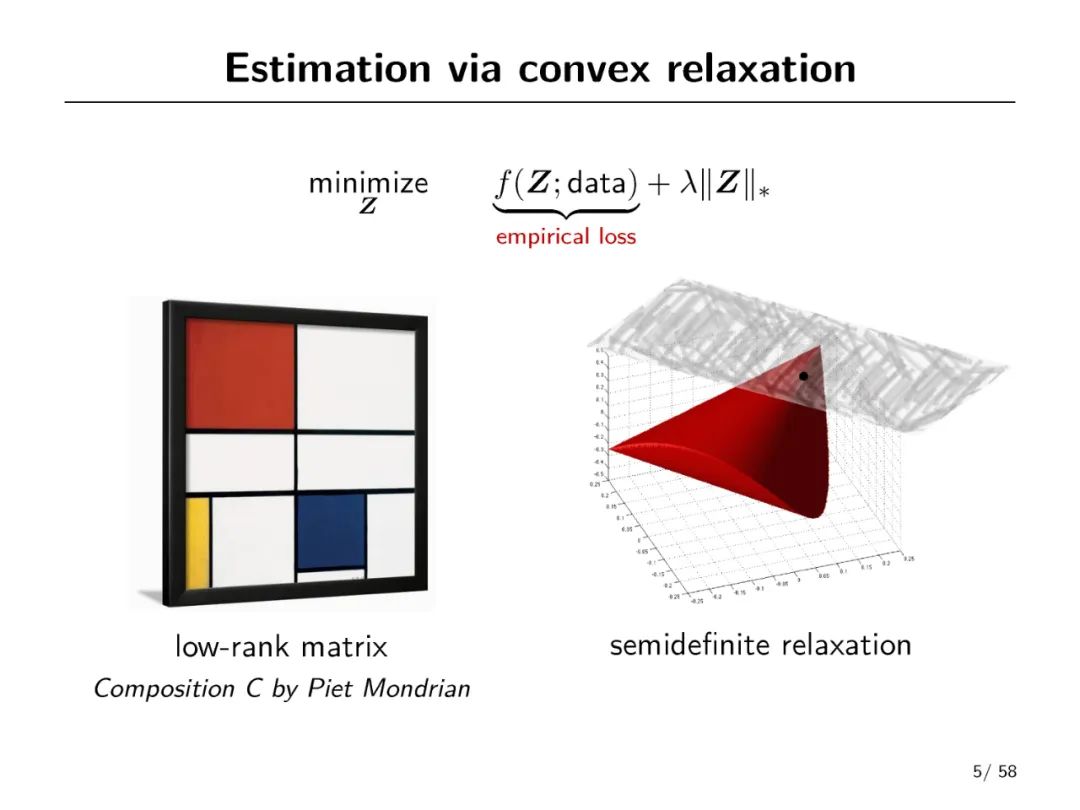
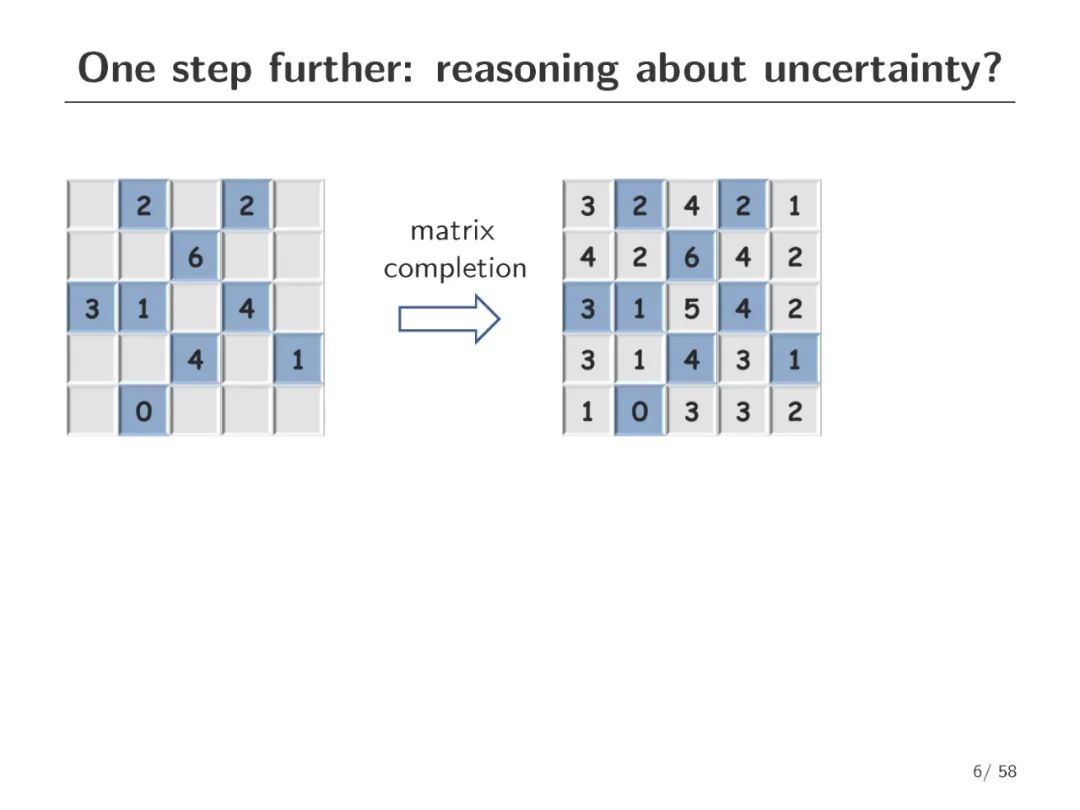
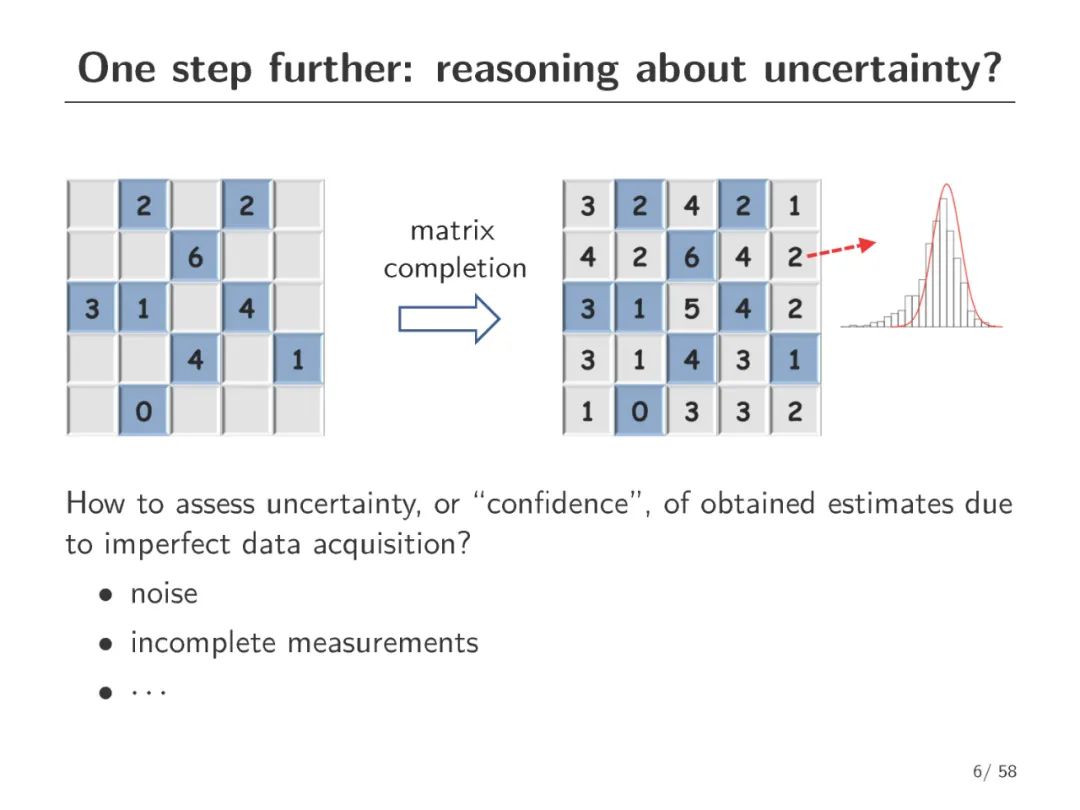
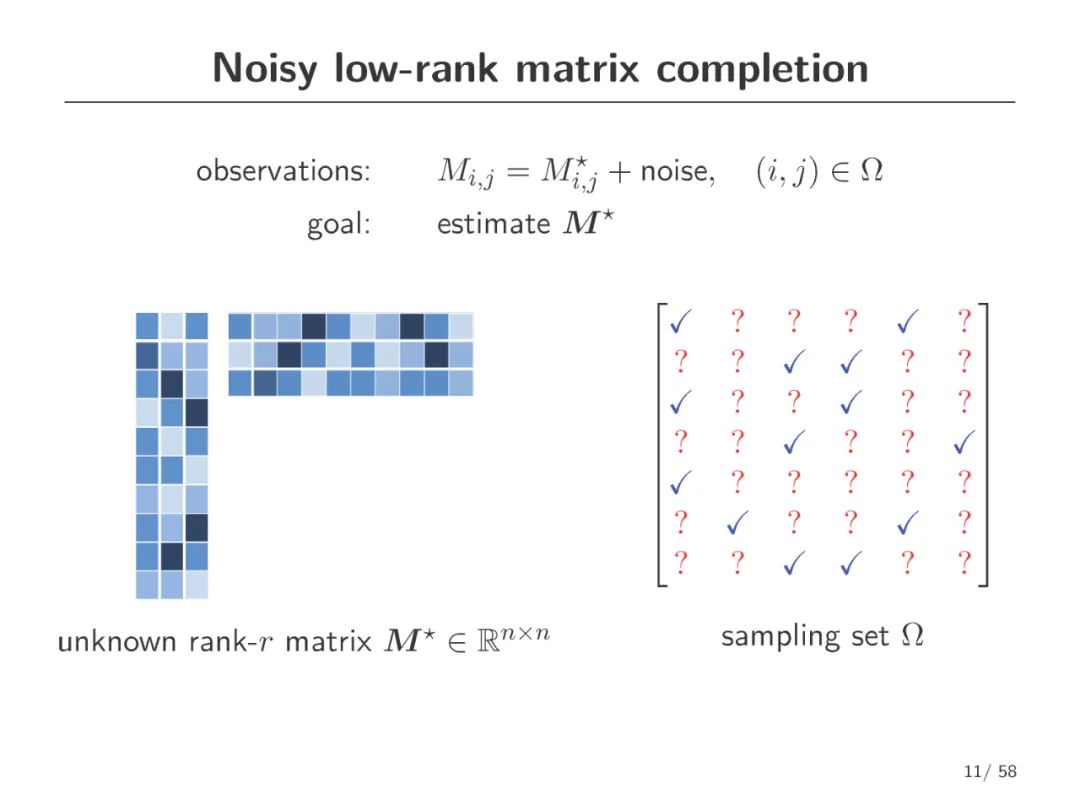
有噪声矩阵补全的目的是估计一个低秩矩阵只给出部分和损坏的项。尽管在设计有效的估计算法方面取得了实质性的进展，但如何评估所获得估计的不确定性以及如何对未知矩阵执行统计推断(例如，为一个未见的条目构造一个有效的和短的置信区间)仍在很大程度上不清楚。这篇报告向有噪声矩阵补全的推理和不确定性量化迈出了一步。我们开发了一个简单的方法来补偿广泛使用的凸估计量和非凸估计量的偏差。所得到的去偏估计量承认了近乎精确的非渐近分布特征，这进而使得诸如缺失项和低秩因子的置信区间/区域的最优构造成为可能。我们的推理过程不依赖于样本分裂，从而避免了数据效率的不必要损失。作为一个副产品，我们得到了对我们的去偏估计的估计精度的一个清晰的表征，据我们所知，这是第一个可证明实现完全统计效率(包括前置常数)的可控算法。本文的分析建立在凸和非凸优化之间的密切联系上。

专知便捷查看

便捷下载，请关注专知公众号（点击上方蓝色专知关注）

• 后台回复“NLMC” 可以获取《【普林斯顿Yuxin Chen】噪声矩阵补全的推理与不确定性量化，117页ppt》专知下载链接索引

专知，专业可信的人工智能知识分发，让认知协作更快更好！欢迎注册登录专知www.zhuanzhi.ai，获取5000+AI主题干货知识资料！

欢迎微信扫一扫加入专知人工智能知识星球群，获取最新AI专业干货知识教程资料和与专家交流咨询！

点击“阅读原文”，了解使用专知，查看获取5000+AI主题知识资源