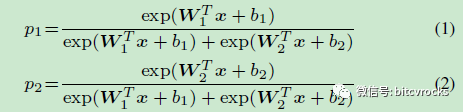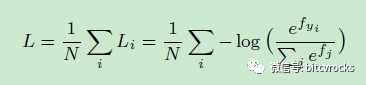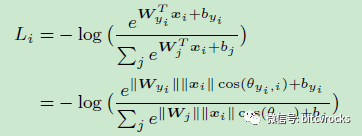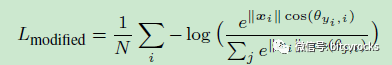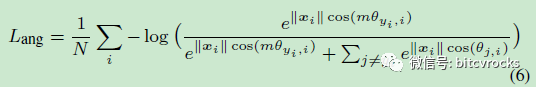读SphereFace: Deep Hypersphere Embedding for FR(CVPR2017 )论文

CVPR2017上一篇关于人脸识别的论文，基于softmax loss提出了一种新的计算损失的方法——angular softmax(A-Softmax），有效的将当前基于欧式空间上的损失度量函数转移到超球体上，同时在一定的度量空间中实现最大类类间距小于最小类内间距 ，从而更好的学习到位于流形域上更具有判别性和更鲁棒的人脸图像特征。

对于二分类问题，基于softmax loss的后验概率如下，如果p1>p2，则分类为类1，反之亦然。 此时的决策边界为 (W1-W2)x+b1-b2=0,其中x为网络最后一个全连接层的输出，wi，bi表示第i类的连接权重和偏置

损失函数为，其中

如果用角度(wi和x之间的夹角)表示概率pi,则：

如果将权值wj归一化使||wj||=1,将bj=0，将其都映射到一个单位球面上，则修正后的损失函数为:

此时的决策边界变为：

而本文旨在学习两个决策边界使分类更加判别,如果属于类别1，则

，此时，比原始的更难。决策边界为，损失函数为

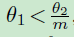
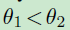
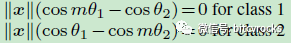
对比总结一下：

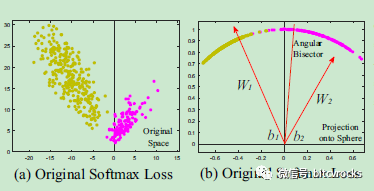
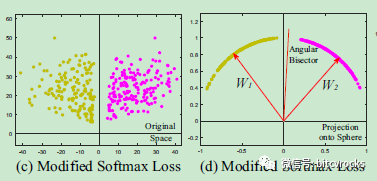
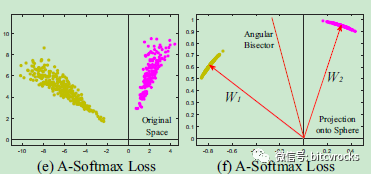
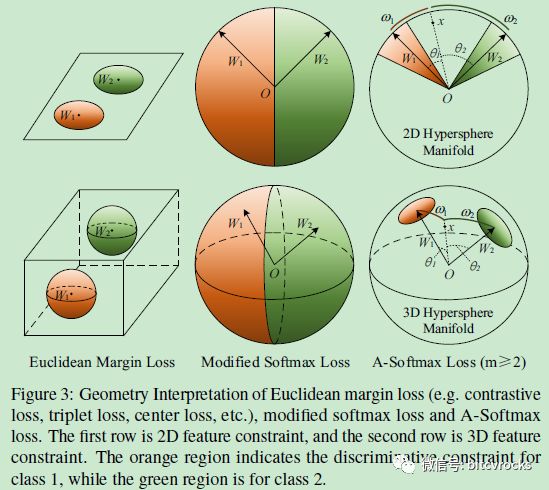
几何表示如下，可以看出来，本文提出的决策边界比其他两种分类边界更具有判别性，并且将原特征空间转换到了超球体流形上，更符合人脸的分布特征，加入m的约束使类内间距更小，类间间距更大。

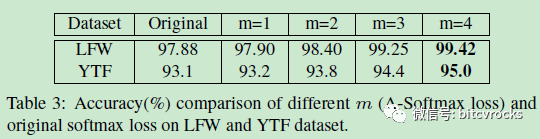
本文通过验证，m对最终分类的结果影响如下，并证明了一般分类下m=4是比较好的选择。

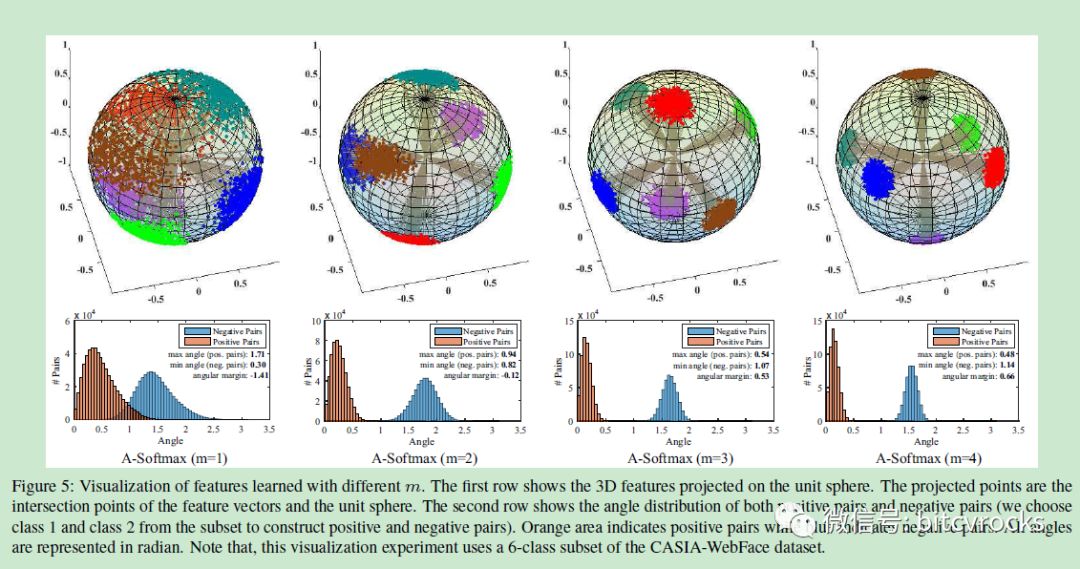
更直观的变现：

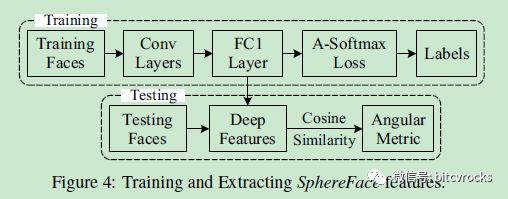
整个实验流程图如下：

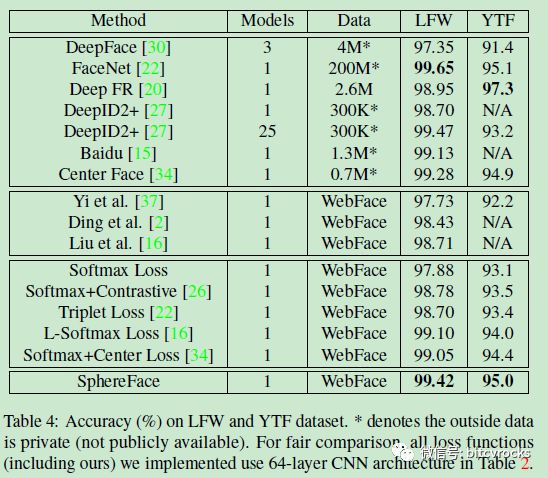
最终实验结果：