蜘蛛仅靠电场就能起飞，连风都不需要，网友：懂了，蜘蛛会用原力

博雯 发自 凹非寺
量子位 | 公众号 QbitAI

现在，科学家们终于搞懂蜘蛛是怎么飞行的了。

哦不对，放错了，是这个：

加州大学的科学们假设，蜘蛛虽然没有翅膀，但却可以依靠自己吐出蛛丝的负电荷，以及地球大气中的正电势场形成的电场来飞行。

基于这一假设，研究团队正经进行了受力分析和数值模拟，实验结果发表在统计物理学、非线性物理领域的期刊Physical Review E上：

对此网友们热烈讨论，并表示：

蜘蛛统治世界的时代已经不远了！

不过在蜘蛛真的统治世界之前，还是让我们先来看看它飞行的原理。

（本文不含任何蜘蛛高清图，读者可放心食用）

蜘蛛如何靠电场飞行？

首先，科学家们建立了一个包括粘性力、蛛丝、蜘蛛的重量和尺寸、静电上升力、排斥力以及弹性弯曲力的三维数值模型，以探索蜘蛛蛛丝在气流中的膨胀和展开的动力学。

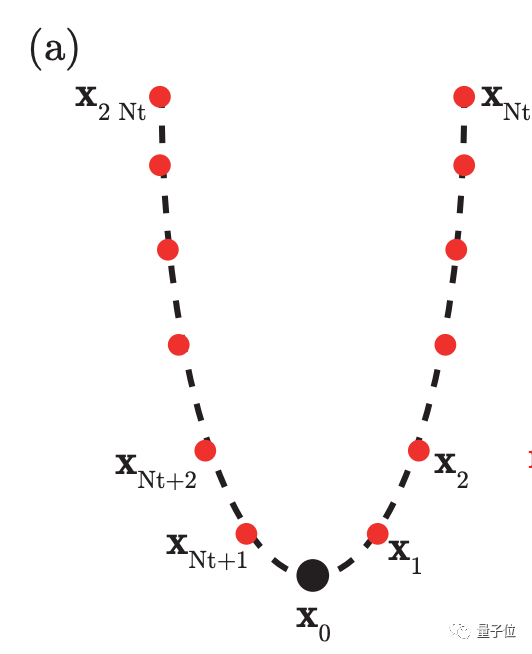
如图所示，一个吐出蛛丝的蜘蛛可以被简化为这样一个模型：

一个直径2毫米左右的实心球体，顶部有2、4或8条距离十分接近（100微米）的丝线，开始为垂直方向，每根线都附有电荷。

关于丝线上是如何带上静电荷的，研究人员认为，这可能是在蜘蛛制作蛛丝的过程中迅速加载电荷，或在制作完成之后，吐丝时与气流产生的摩擦。

为了研究流体结构与电场的相互作用，数值模拟涉及到三个部分：

• 通过离散弹性棒（DER）方法计算线的弹性变形，即弯曲、扭曲和拉伸等等

• 阻力理论（RFT）方法计算蜘蛛和丝线上的流体动力学的粘性力

• 由大气电位梯度和丝线电荷引起的静电力

具体而言，在数值模拟中，蜘蛛被建模为一个弹性棒网络。

其中一个节点x₀代表蜘蛛身体，每条线有N_t个节点。对于一个有n_t条线的蜘蛛，节点的总数是n_tN_t+1，两个连续节点之间的向量是边，每个线程由N_t条边组成：

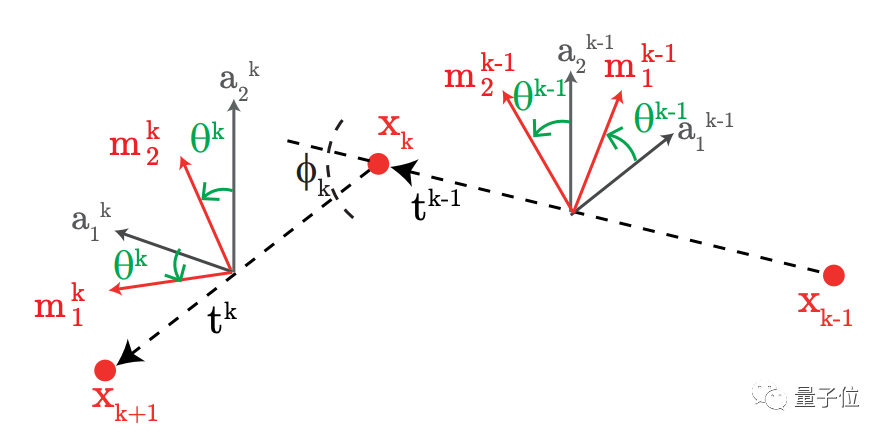
边的拉伸、弯曲、旋转则采用这样一种框架来分析：

在模拟实验中，蜘蛛从地面静止，然后开始被电场“提起”。

带电的、最初的丝线会附着在蜘蛛身上，丝线之间的相互排斥会导致它们在一段时间内分开。随着蜘蛛向上加速，向下的阻力会增加，和蜘蛛本身的重力一起抵消向上的力。

最终，团队中的研究人员Charbel Habchi下了定论：

我们认为，至少小型蜘蛛在没有任何上升气流帮助的情况下，完全可以通过电场悬浮。而体型较大的蜘蛛则需要向上气流的推动。

“懂了，蜘蛛会用原力”

对于这项研究，广大网友身体力行地上演了一波真·震惊体。

我震惊地张大了嘴，但又害怕有一百只小蜘蛛飞进来。

巨大的蜘蛛群笼罩并袭击了整个北乔治亚区和周边地区。这真是个不错的科幻概念。

下面有人回复道：别再说了，我要yue了……

而星球大战梗也虽迟但到：

所以蜘蛛会使用原力。

。

论文：
https://journals.aps.org/pre/abstract/10.1103/PhysRevE.105.034401

参考链接：
[1]https://physics.aps.org/articles/v15/31
[2]https://www.reddit.com/r/science/comments/takn5y/spiders_use_electric_fields_to_fly_and_we_may/

— 完 —

「人工智能」、「智能汽车」微信社群邀你加入！

欢迎关注人工智能、智能汽车的小伙伴们加入我们，与AI从业者交流、切磋，不错过最新行业发展&技术进展。

ps.加好友请务必备注您的姓名-公司-职位哦~

点这里👇关注我，记得标星哦～

一键三连「分享」、「点赞」和「在看」

科技前沿进展日日相见~