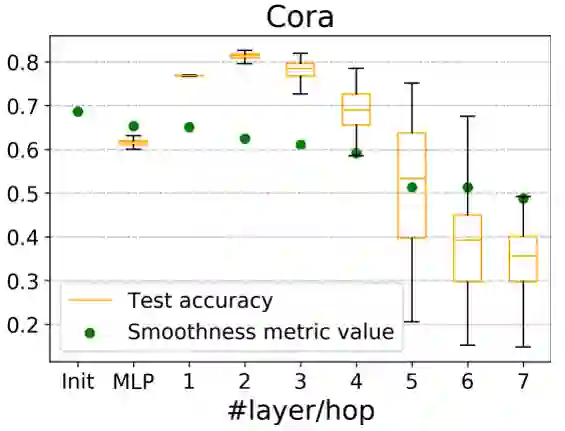
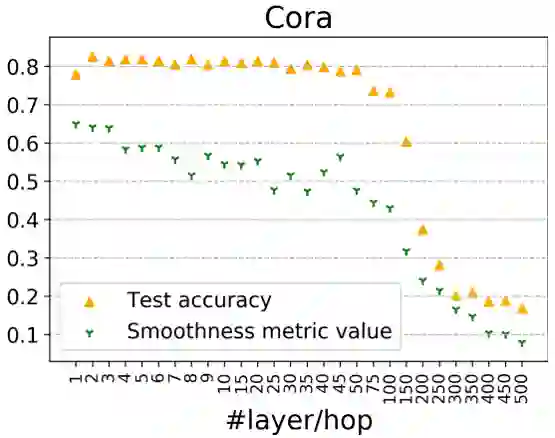
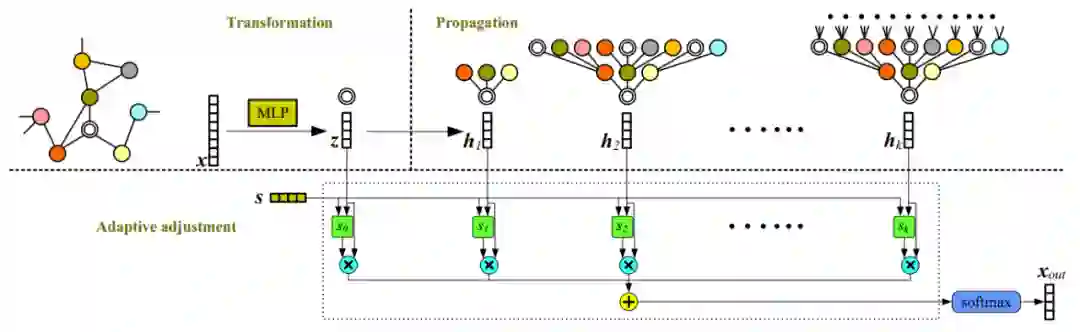
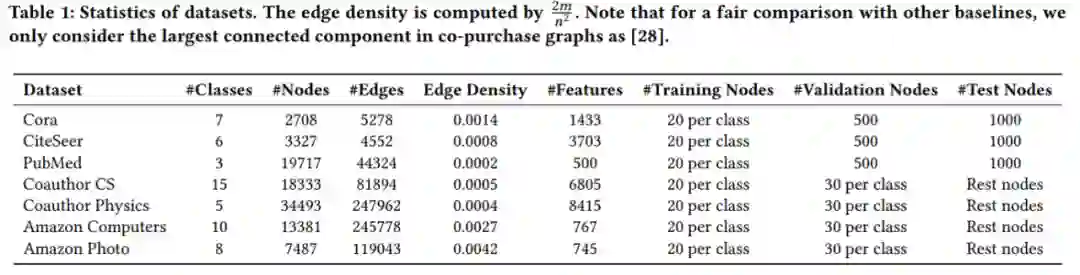
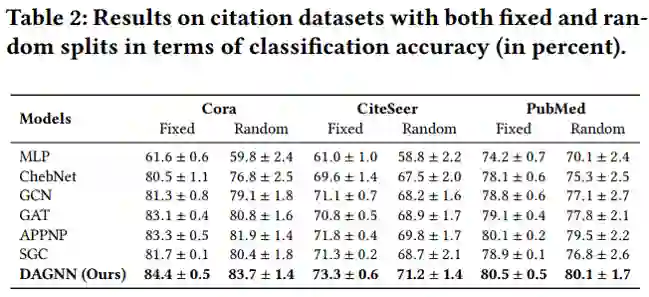
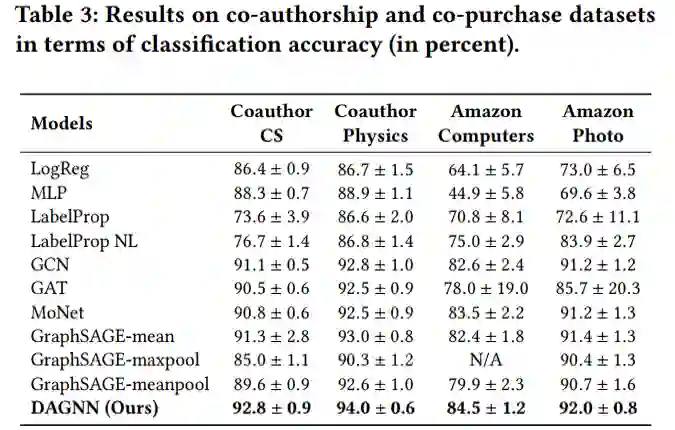
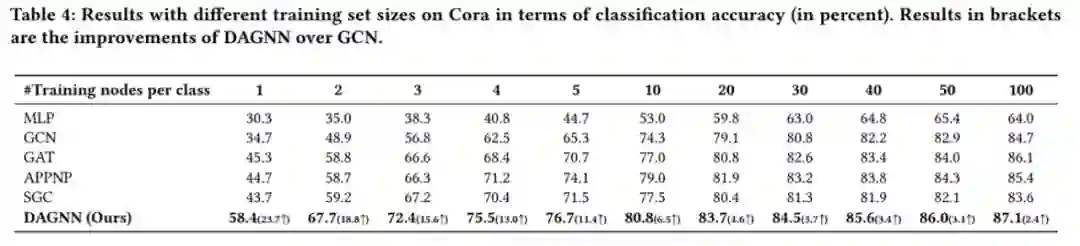
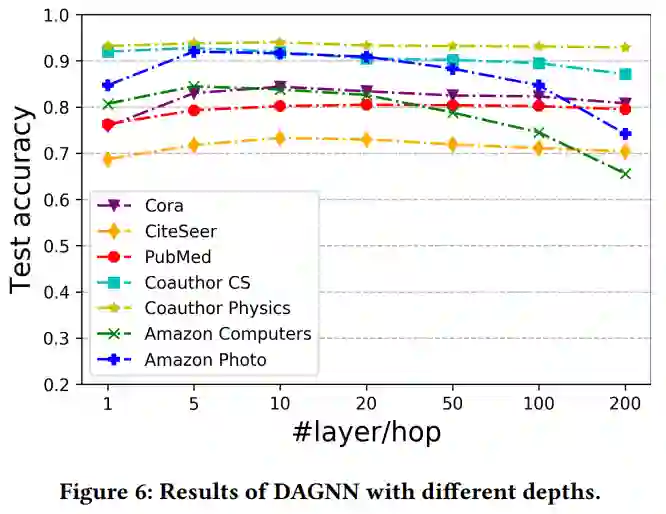
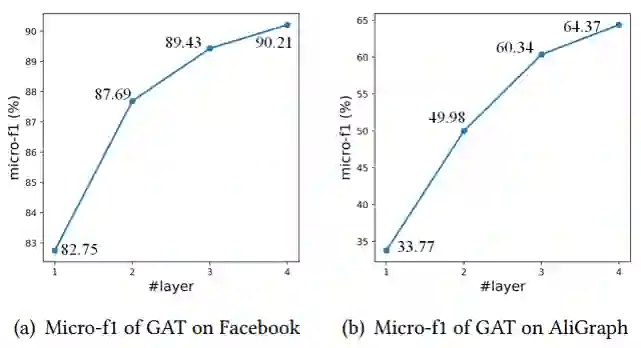
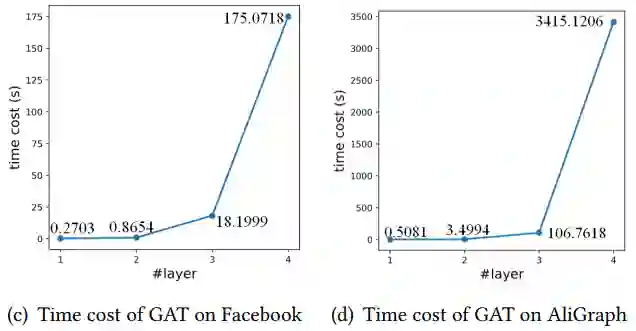
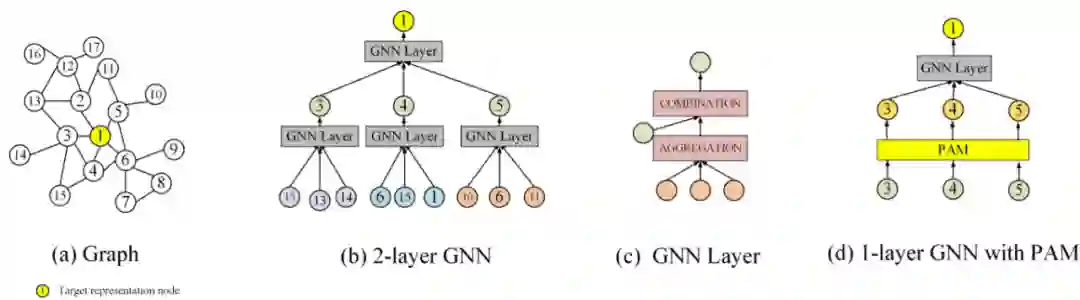
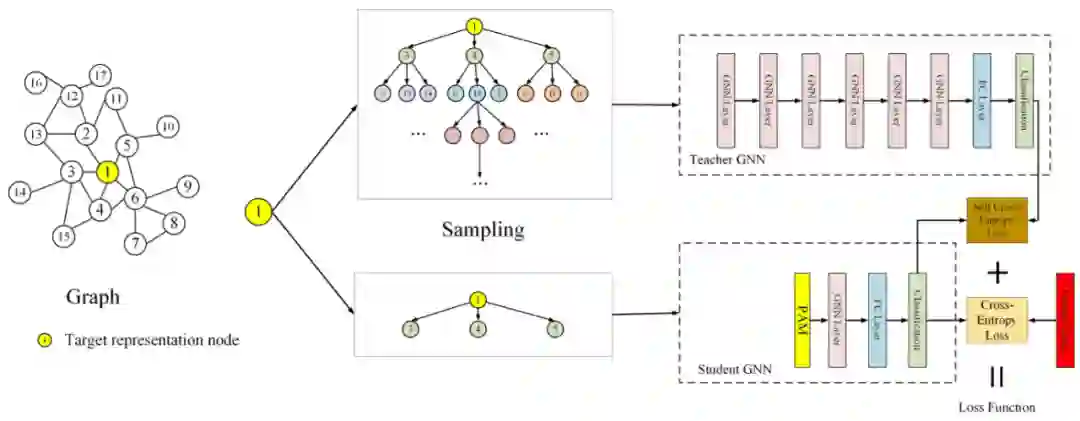
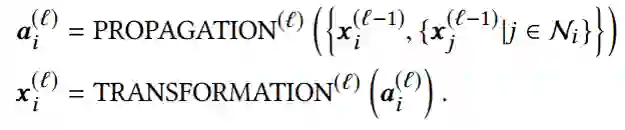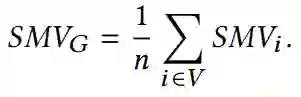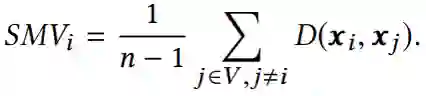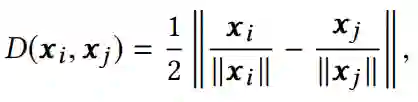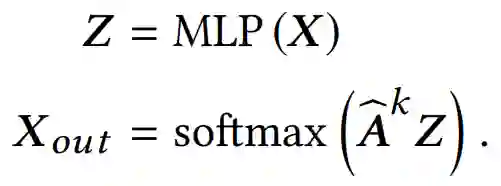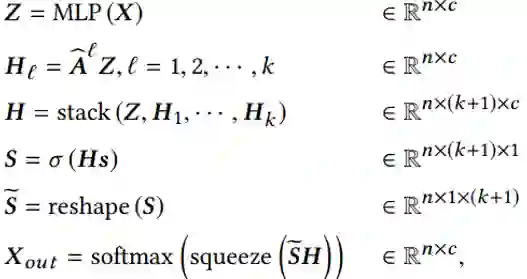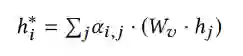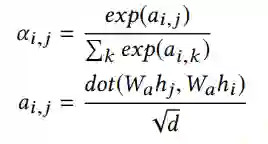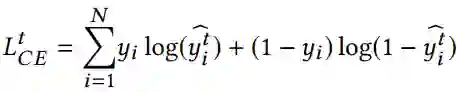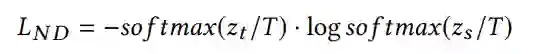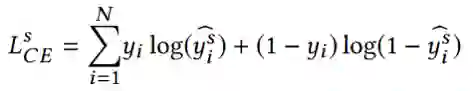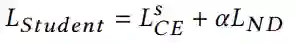【KDD2020】 深度图神经网络专题论文解读
专知便捷查看
便捷下载,请关注专知公众号(点击上方蓝色专知关注)
后台回复“GNN2” 可以获取《【KDD2020】 深度图神经网络专题论文解读》专知下载链接索引


登录查看更多
相关内容
Arxiv
0+阅读 · 2020年11月30日